fit[, resid := rating - clamp(mu + a + b)]25 Latent Factor Models
In the previous chapter, we described how the model:
\[ Y_{ij} = \mu + \alpha_i + \beta_j + \varepsilon_{ij} \]
can be used to model movie ratings and help make useful predictions. This model accounts for user differences through \(\alpha_i\) and movie effects through \(\beta_j\). However, the model ignores an important source of information related to the fact that groups of movies have similar rating patterns and groups of users have similar rating patterns as well.
To see an example of this, we compute residuals:
\[ r_{ij} = y_{ij} - (\hat{\mu} + \hat{\alpha}_i + \hat{\beta}_j) \]
using the mu, a and b computed in the previous chapter,
and see how the residuals for three different movies correlate with The Godfather:
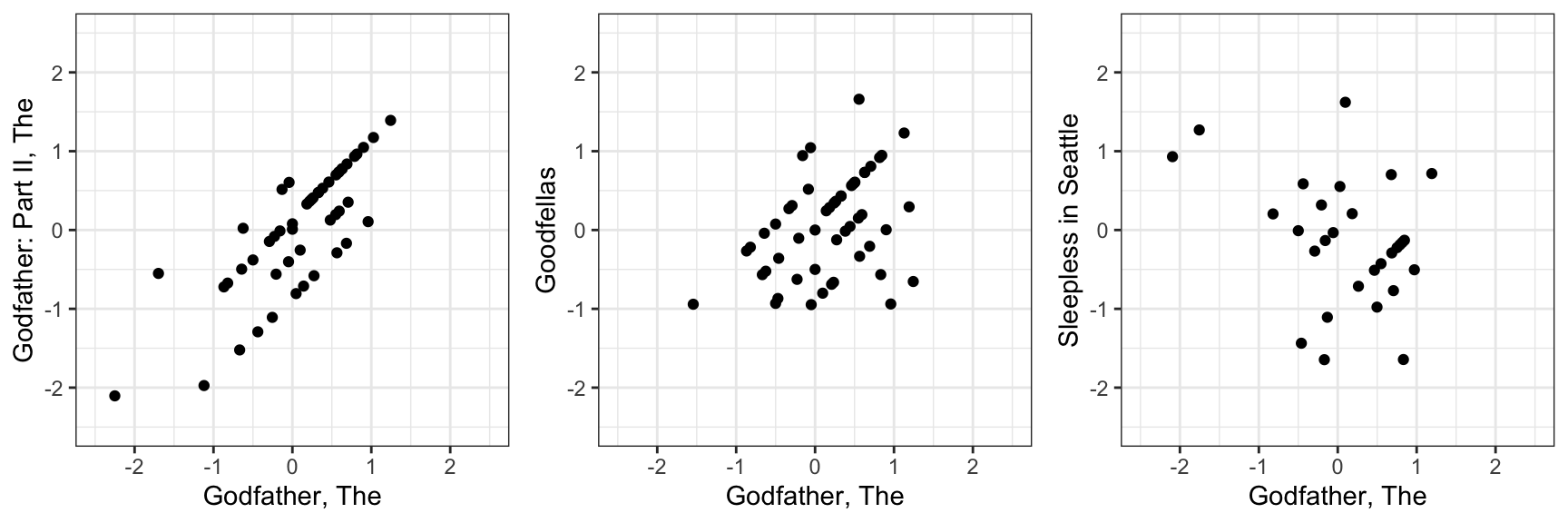
We see that the correlation varies from very strong positive to negative across the other three movies.
In this chapter, we introduce Latent Factor Models, an approach that captures these correlation patterns and improves prediction accuracy. We present the ideas in the context of movie recommendation systems, where latent factors represent hidden groups of users with similar preferences and movie characteristics. We highlight the connection between factor models and Principal Component Analysis (PCA), showing how both reduce dimensionality by uncovering structure in the data. Finally, we close the chapter by introducing a related technique, the Singular Value Decomposition (SVD), which provides a general mathematical framework underlying both PCA and latent factor methods.
25.1 Factor analysis
We start with a simple simulated example. Specifically, we simulate ratings \(Y_{ij}\) for six movies and 120 users. For simplicity we assume that these ratings have been adjusted for the movie and user effects described in Chapter 24. We stored the results for 120 user and 6 movie effects in the object y:
dim(y)
#> [1] 120 6If we examine the correlation between movies based on user ratings, we notice a pattern:
cor(y)
#> Godfather Godfather 2 Goodfellas Scent of a Woman
#> Godfather 1.000 0.671 0.558 -0.527
#> Godfather 2 0.671 1.000 0.471 -0.450
#> Goodfellas 0.558 0.471 1.000 -0.888
#> Scent of a Woman -0.527 -0.450 -0.888 1.000
#> You've Got Mail -0.734 -0.649 -0.487 0.451
#> Sleepless in Seattle -0.721 -0.739 -0.505 0.475
#> You've Got Mail Sleepless in Seattle
#> Godfather -0.734 -0.721
#> Godfather 2 -0.649 -0.739
#> Goodfellas -0.487 -0.505
#> Scent of a Woman 0.451 0.475
#> You've Got Mail 1.000 0.756
#> Sleepless in Seattle 0.756 1.000It appears that ratings are positively correlated within genres, for example, among mob movies or among romance movies, and negatively correlated across the two genres. In statistics, such patterns are often explained by factors: unobserved, or latent, variables that account for the correlations or associations among the observed variables. Under certain assumptions, which we will describe below, these latent factors can be estimated from the data and used to capture the underlying structure driving the correlations.
One approach is to use our knowledge of movies genres to define a factor that distinguishes between mob and romance movies:
q <- c(1, 1, 1, -1, -1, -1)We code mob movies with -1 and romance movies with 1.
To quantify each user’s genre preference, we fit a linear model for every user \(i\):
Here, we use -1 in the formula because the residuals have mean 0 and no intercept is needed.
There is a faster way to make this computation using linear algebra. This is because the lm function is computing the least squares estimates by taking the derivative of the sum of squares, equaling it to 0, and noting the solution \(\hat{\boldsymbol{\beta}}_i\) satisfies:
\[ (\mathbf{q}^\top\mathbf{q}) \, \hat{\boldsymbol{\beta}}_i = \mathbf{q}^\top \mathbf{y}_i \]
with \(\mathbf{y}_i\) column vector represeting the row of y passed to y_i in the apply function. Because \(\mathbf{q}\) does not change for each user, rather than have lm recompute the equation for each user, we can perform the calculation on each row of y to get the \(\beta_i\) for all users \(i\) like this:
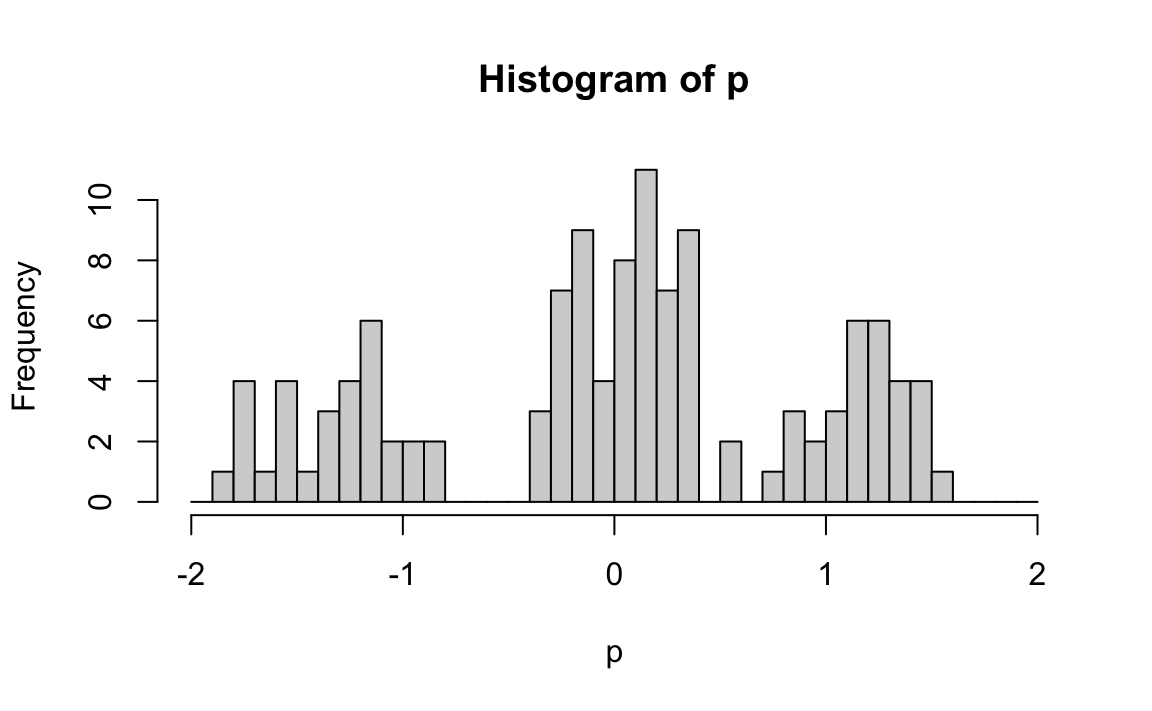
The resulting vector p represents, for each user, the difference in average ratings between mob and romance movies. A positive value indicates a preference for mob movies, a negative value indicates a preference for romance movies, and values near 0 suggest no strong preference. The histogram below shows users cluster into these three type:
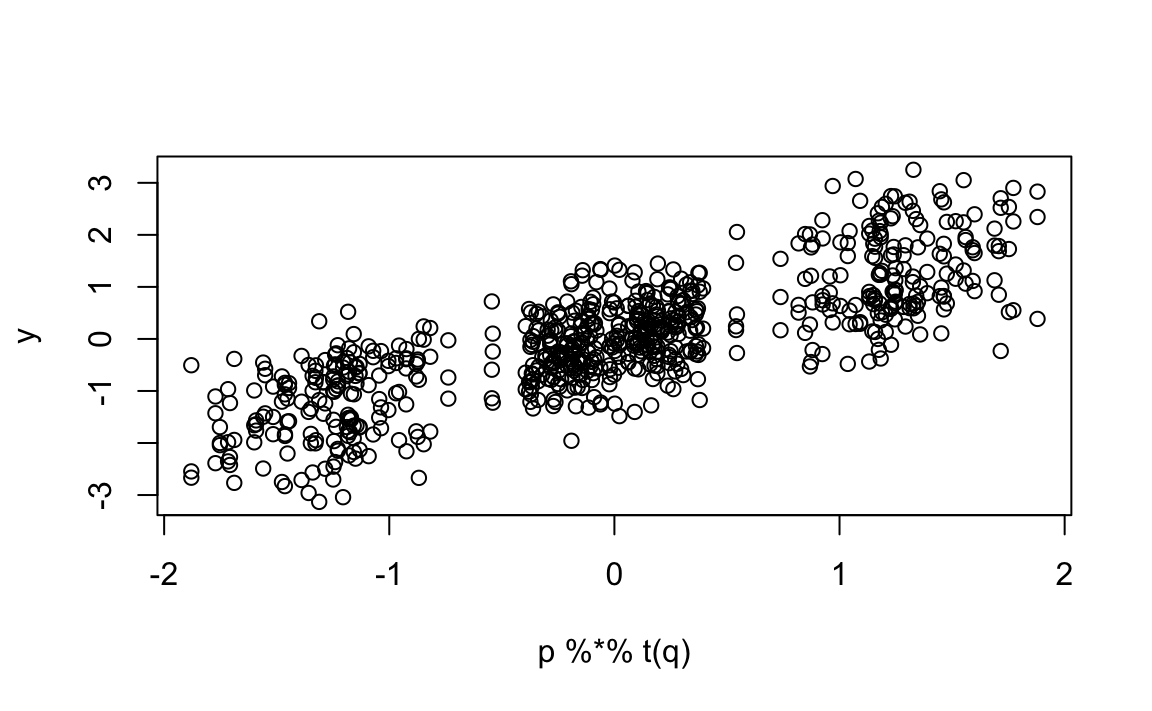
To see that we can approximate \(Y_{ij}\) with \(p_iq_j\) we convert the vectors to matrices and use linear algebra:
However, after removing this mob/romance effect, we still see structure in the correlation:
cor(y - p %*% t(q))
#> Godfather Godfather 2 Goodfellas Scent of a Woman
#> Godfather 1.000 0.185 -0.545 0.557
#> Godfather 2 0.185 1.000 -0.618 0.594
#> Goodfellas -0.545 -0.618 1.000 -0.671
#> Scent of a Woman 0.557 0.594 -0.671 1.000
#> You've Got Mail -0.280 -0.186 0.619 -0.641
#> Sleepless in Seattle -0.198 -0.364 0.650 -0.656
#> You've Got Mail Sleepless in Seattle
#> Godfather -0.280 -0.198
#> Godfather 2 -0.186 -0.364
#> Goodfellas 0.619 0.650
#> Scent of a Woman -0.641 -0.656
#> You've Got Mail 1.000 0.353
#> Sleepless in Seattle 0.353 1.000This structure seems to be driven by Al Pacino being in the movie or not. This implies we could add another factor in a second column:
We can then, for each factor, obtain an estimates preference for each user:
We use the transpose t because apply binds results into columns and we want a row for each user.
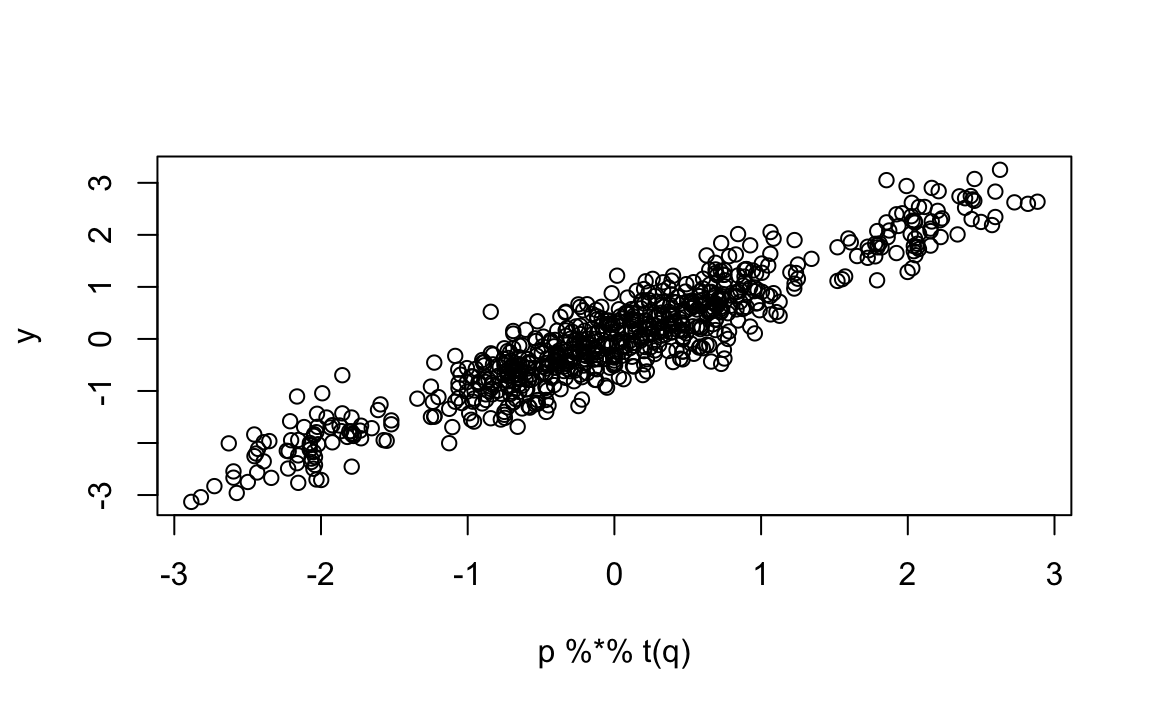
Our approximation based on two factors does an even better job of predicting how our residuals deviate from 0:
This approximation with two factors can be written as:
\[ Y_{ij} \approx p_{i1}q_{j1} + p_{i2}q_{j2}, i = 1 \dots, I \mbox{ and } j = 1, \dots, J \] with \(I\) the number of users and \(J\) the number of movies.
Using matrix representation we can rewrite the above question like this:
\[ \mathbf{Y} \approx \mathbf{P}\mathbf{Q}^\top \] with \(\mathbf{Y}\) an \(I\times J\) matrix with entries \(Y_{ij}\), \(\mathbf{P}\) a \(I\times K\) matrix with entries \(p_{ik}\), and \(\mathbf{Q}\) a \(J\times K\) matrix with entries \(q_{jk}\).
This analysis provides insights into the process generating our data since \(\mathbf{P}\) contains user-specific parameters and \(\mathbf{Q}\) contains movie-specific parameters. The approach is often referred to as matrix factorization because the rating matrix has been factorized into two lower-dimensional, interpretable matrices.
Note that the apporach also provides compression since the \(120 \times 6 = 720\) observations can be well approximated by a matrix multiplication of a \(120 \times 2\) matrix \(\mathbf{P}\) and a \(6 \times 2\) matrix \(\mathbf{Q}\), a total of 252 parameters.
In our example with simulated data, we deduced the factors \(\mathbf{p}_1\) and \(\mathbf{p}_2\) from the sample correlation and our knowledge of movies. These ended up working well. However, in general deducing factors is not this easy. Furthermore, factors that provide good approximation might be more complicated than containing just two values. For example, The Godfather III has a romantic subplot so we might not know what value to assign it in q.
So, can we estimate the factors? A challenge is that if \(\mathbf{P}\) is unknown, our model is no longer linear: we can’t use lm to estimate both \(\mathbf{P}\) and \(\mathbf{Q}\). In the next sections, we describe how PCA can be used to estimate \(\mathbf{P}\) and \(\mathbf{Q}\).
25.2 Connection to PCA
Notice that in Section 23.5 we learned that if we perform PCA on the matrix \(\boldsymbol{\varepsilon}\), we obtain a transformation \(\mathbf{V}\) that permits us to rewrite:
\[ \mathbf{Y} = \mathbf{Z} \mathbf{V}^\top \]
with \(\mathbf{Z}\) the matrix of principal components.
Let’s perform PCA and examine the results:
pca <- prcomp(y, center = FALSE)First, notice that the first two PCs explain over 85% of the variability:
pca$sdev^2/sum(pca$sdev^2)
#> [1] 0.6939 0.1790 0.0402 0.0313 0.0303 0.0253Next, notice that the first column of \(\mathbf{V}\):
pca$rotation[,1]
#> Godfather Godfather 2 Goodfellas
#> 0.306 0.261 0.581
#> Scent of a Woman You've Got Mail Sleepless in Seattle
#> -0.570 -0.294 -0.300is assigning positive values to the mob movies and negative values to the romance movies.
The second column:
pca$rotation[,2]
#> Godfather Godfather 2 Goodfellas
#> 0.354 0.377 -0.382
#> Scent of a Woman You've Got Mail Sleepless in Seattle
#> 0.437 -0.448 -0.442is coding for Al Pacino movies.
PCA is automatically discovering the structure we inferred using our knowledge of the movies. This is not a coincidence, there is a mathematical connection that explains why PCA aligns with these latent patterns. To see this assume that data \(\mathbf{Y}\) follows the model:
\[ Y_{ij} = \sum_{k=1}^K p_{ik}q_{jk} + \varepsilon_{ij}, i=1,\dots,I, \, j = 1,\dots J \mbox{ or } \mathbf{Y} = \mathbf{P}\mathbf{Q} ^\top + \boldsymbol{\varepsilon} \] with the constraint
\[ \mathbf{Q}^\top\mathbf{Q} = \mathbf{I} \]
To understand why we need this constraint, notice that without it the model is not uniquely defined, it is not identifiable. For example, we can multiply any column of \(\mathbf{P}\) by a constant \(c > 0\) and divide the corresponding column of \(\mathbf{Q}\) by the same constant, and the product \(\mathbf{P}\mathbf{Q}^\top\) remains unchanged. This constraint removes the scaling ambiguity and ensures that the factorization has a well-defined form.
The first \(K\) columns of the principal components and the associated rotation matrix provide estimates of \(\mathbf{P}\) and \(\mathbf{Q}\), respectively. In other words, PCA can be viewed as a special case of latent factor modeling where the latent factors are chosen to be orthogonal and ordered by the variance they explain. This explains why PCA naturally recovers interpretable patterns, such as genre preferences or actor-specific effects, without us explicitly coding them into the model.
Another way to see this connection is through optimization. PCA can be formulated as the solution to a least squares problem: among all possible \(K\)-dimensional projections of the data, PCA finds the one that minimizes the reconstruction error, that is, the sum of squared differences between the original data \(\mathbf{Y}\) and its approximation \(\mathbf{P}\mathbf{Q}^\top\). In this sense, PCA provides the best rank-\(K\) approximation of \(\mathbf{Y}\) in the least squares sense.
This dual interpretation—both as a factor model and as a least squares optimizer—highlights why PCA is such a powerful tool for uncovering hidden structure in high-dimensional data: it compresses the data efficiently while also providing factors that capture the dominant sources of variation.
Even with the orthogonality constraint, the solution is not completely unique.
There remains a sign indeterminacy: we can flip the sign of any column in \(\mathbf{P}\) and the corresponding column in \(\mathbf{Q}\) (multiply one by \(-1\) and the other by \(-1\)) without changing the product \(\mathbf{P}\mathbf{Q}^\top\).
Thus, the factorization is identifiable only up to these sign changes.
25.3 Case study: movie recommendations
If we examine the correlation structure of the movies we simulated earlier, we again observe clear patterns:
#> Goodfellas Godfather: Part II, The
#> Goodfellas 1.0000 0.486
#> Godfather: Part II, The 0.4856 1.000
#> You've Got Mail -0.2657 -0.246
#> Scent of a Woman 0.0789 0.235
#> Sleepless in Seattle -0.4302 -0.474
#> Godfather, The 0.4977 0.837
#> You've Got Mail Scent of a Woman
#> Goodfellas -0.266 0.0789
#> Godfather: Part II, The -0.246 0.2348
#> You've Got Mail 1.000 -0.3571
#> Scent of a Woman -0.357 1.0000
#> Sleepless in Seattle 0.415 -0.5178
#> Godfather, The -0.348 0.5479
#> Sleepless in Seattle Godfather, The
#> Goodfellas -0.430 0.498
#> Godfather: Part II, The -0.474 0.837
#> You've Got Mail 0.415 -0.348
#> Scent of a Woman -0.518 0.548
#> Sleepless in Seattle 1.000 -0.441
#> Godfather, The -0.441 1.000This suggests that we can improve the predictions from Chapter 24 by leveraging these correlations. For instance, ratings for The Godfather should inform ratings for The Godfather II. But what other patterns might help?
To account for interaction such as these we use a latent factor model. Specifically, we extend the model from Chapter 24 to include factors that capture similarities between movies:
\[ Y_{ij} = \mu + \alpha_i + \beta_j + \sum_{k=1}^K p_{ik}q_{jk} + \varepsilon_{ij} \]
Recall that, as explained in the previous chapter, we do not observe all \((i,j)\) combinations. Writing the data as an \(I \times J\) matrix \(\mathbf{Y}\), with \(I\) users and \(J\) movies, would produce many missing values.
However, the sum \(\sum_{k=1}^K p_{ik}q_{jk}\) can be expressed as the matrix product \(\mathbf{P}\mathbf{Q}^\top\), where \(\mathbf{P}\) is an \(I \times K\) matrix and \(\mathbf{Q}\) is a \(J \times K\) matrix. Estimating all parameters fills in every cell of the \(I \times J\) matrix, giving predictions for all \((i,j)\) pairs.
Given the large number of parameters and the sparsity of the data, especially for movies with few ratings, it is appropriate to use penalized least squares. We minimize:
\[ \frac{1}{N} \sum_{i,j} \left[Y_{ij} - \left(\mu + \alpha_i + \beta_j + \sum_{k=1}^K p_{ik}q_{jk}\right)\right]^2 + \lambda_1 \left( \|\boldsymbol{\alpha}\|^2 + \|\boldsymbol{\beta}\|^2 \right) + \lambda_2 \left( \sum_{k=1}^K \|\mathbf{p}_k\|^2+ \sum_{k=1}^K \|\mathbf{q}_k\|^2 \right) \]
Here, \(N\) is the number of observed ratings, \(I\) the number of users, and \(J\) the number of movies. The vectors \(\boldsymbol{\alpha}\) and \(\boldsymbol{\beta}\) are the user and movie effects, \(\boldsymbol{\alpha} = (\alpha_1,\dots,\alpha_I)^\top\) and \(\boldsymbol{\beta} = (\beta_1,\dots,\beta_J)^\top\). The vectors \(\mathbf{p}_k = (p_{1,k}, \dots, p_{ik})^\top\) and \(\mathbf{q}_k = (q_{1,k}, \dots, q_{jk})^\top\) are the \(k\)-th latent factor components. Recall that \(|\boldsymbol{\alpha}|^2\) denotes the sum of squares, \(\sum_{i=1}^I \alpha_i^2\).
We use two penalties: \(\lambda_1\) for the linear effects (\(\alpha\)s and \(\beta\)s), and \(\lambda_2\) for the latent factors. This lets us regularize the two components differently, reflecting their distinct roles in the model.
How do we estimate the parameters in this model? As mentioned, the challenge comes from the fact that both the \(p\)s and \(q\)s are unknown and appear multiplied together, making the model nonlinear in its parameters. In earlier sections, we highlighted the connection between factor analysis and Principal Component Analysis (PCA), and showed that in settings with complete data, PCA can be used to estimate the latent factors of a factor analysis model.
However, recommendation systems present a critical complication: the rating matrix is extremely sparse. Most users only rate a small subset of movies, so the data matrix has many missing entries. PCA and related approaches require a fully observed matrix, so they cannot be applied directly in this context. In addition, while PCA provides least squares estimates, here we want to use penalized least squares, which allows us to regularize the parameters and avoid overfitting when the data for some users or movies are limited.
To address these challenges, we turn to an iterative optimization method called Alternating Least Squares (ALS). The key idea is to alternately estimate \(\mathbf{P}\) and \(\mathbf{Q}\): fix one matrix and solve for the other using penalized least squares, then switch. This alternating approach also extends easily to penalized versions of the model, where user/movie effects and latent factors are regularized separately. For these reasons, ALS has become one of the standard approaches for fitting latent factor models in recommendation systems, where sparsity makes direct application of PCA infeasible.
The dslabs package provides the fit_recommender_model function, which implements this approach which we use here:
fit <- with(train_set, fit_recommender_model(rating, userId, movieId, min_ratings = 20, reltol = 1e-5))We can now build a prediction for the test set based on the estimated parameters and note that it improves prediction:
resid <- with(test_set, rating -
clamp(fit$mu + fit$a[as.character(userId)] + fit$b[as.character(movieId)] +
rowSums(fit$p[as.character(userId),] * fit$q[as.character(movieId),])))
rmse(resid)
#> [1] 0.86Note that further gains are possible by optimizing the penalty terms and tuning the number of latent factors. The team from BellKor, who ultimately won the Netflix Prize, had another key insight that further improved prediction: they accounted for the information hidden in the missing ratings. In practice, users tend to avoid movies they expect to dislike, so the absence of a rating is not random but itself carries signal. Incorporating this additional structure into the model helped them achieve state-of-the-art performance.
25.3.1 Visualizing factors
Examining the estimated movie factors \(\mathbf{q}_k\) reveals that they are interpretable.
The estimates for these factors are contained in fit$q. Because some movies do not have enough ratings to stably estimate latent factors, the fit_recommender_model function excludes these movies from the estimation. We therefore obtain the estimated movie factors \(\mathbf{q}_k\) using:
factors <- fit$q[fit$n_item >= fit$min_ratings,] To make interpretation easier, we replace the row names (which are movie IDs) with movie titles:
Plotting the first two factors reveals several insights. As shown below, the movies highlighted in blue demonstrate that mob films cluster together, while romance films without Al Pacino also cluster together:
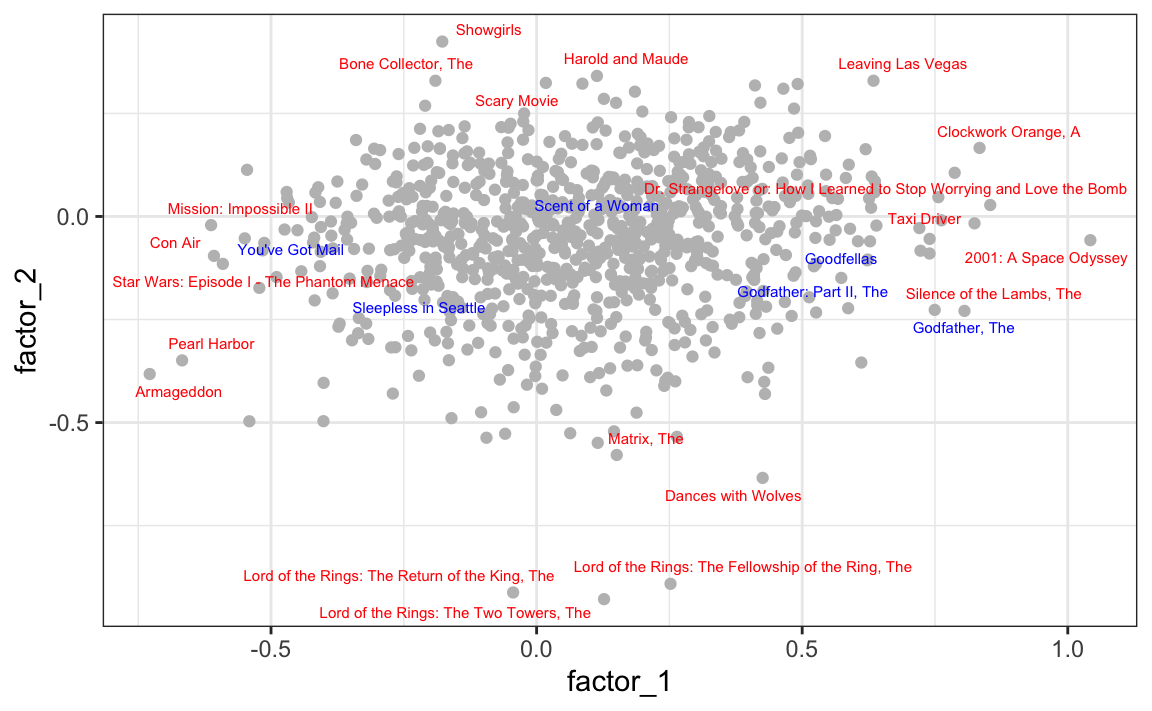
Looking at the movies with the most extreme factor values confirms that the dimensions are interpretable. The first factor separates critically acclaimed films:
from Hollywood blockbusters:
The second factor contrasts cult or offbeat films:
with epics:
These results demonstrate that the latent factors capture meaningful distinctions in film genres and styles, showing how matrix factorization can uncover interpretable structure from sparse rating data.
25.4 Singular Value Decomposition
A related technique often used in latent factor analysis is the Singular Value Decomposition (SVD). It states any \(N \times p\) matrix can be written:
\[ \mathbf{Y} = \mathbf{U}\mathbf{D}\mathbf{V}^\top \]
where \(\mathbf{U}\) is an orthogonal \(N \times p\) matrix, \(\mathbf{V}\) an orthogonal \(p \times p\) matrix, and \(\mathbf{D}\) diagonal with \(d_{1,1} \geq d_{2,2} \geq \dots \geq d_{p,p}\). SVD is connected to PCA because \(\mathbf{V}\) provides the rotations for the principal components, while \(\mathbf{U}\mathbf{D}\) are the principal components themselves. Squaring the diagonal entries of \(\mathbf{D}\) gives the sums of squares:
\[ \mathbf{U}^\top \mathbf{D} \mathbf{U} = \mathbf{D}^2 \]
In R, we can compute the SVD with svd and confirm its relationship to PCA:
As an optimization, note that s$u %*% diag(s$d) can be written more efficiently as:
sweep(s$u, 2, s$d, "*")25.5 Exercises
In this exercise set, we use the singular value decomposition (SVD) to estimate factors in an example related to the first application of factor analysis: finding factors related to student performance in school.
We construct a dataset that represents grade scores for 100 students in 24 different subjects. The overall average has been removed so this data represents the percentage points each student received above or below the average test score. So a 0 represents an average grade (C), a 25 is a high grade (A+), and a -25 represents a low grade (F). You can simulate the data like this:
set.seed(1987)
n <- 100
k <- 8
Sigma <- 64 * matrix(c(1, .75, .5, .75, 1, .5, .5, .5, 1), 3, 3)
m <- MASS::mvrnorm(n, rep(0, 3), Sigma)
m <- m[order(rowMeans(m), decreasing = TRUE),]
y <- m %x% matrix(rep(1, k), nrow = 1) +
matrix(rnorm(matrix(n * k * 3)), n, k * 3)
colnames(y) <- c(paste(rep("Math",k), 1:k, sep="_"),
paste(rep("Science",k), 1:k, sep="_"),
paste(rep("Arts",k), 1:k, sep="_"))Our goal is to describe the student performances as succinctly as possible. For example, we want to know if these test results are all simply random independent numbers. Are all students just about as good? Does being good in one subject imply one will be good in another? How does the SVD help with all this? We will go step by step to show that with just three relatively small pairs of vectors, we can explain much of the variability in this \(100 \times 24\) dataset.
You can visualize the 24 test scores for the 100 students by plotting an image:
my_image <- function(x, zlim = range(x), ...){
colors = rev(RColorBrewer::brewer.pal(9, "RdBu"))
cols <- 1:ncol(x)
rows <- 1:nrow(x)
image(cols, rows, t(x[rev(rows),,drop=FALSE]), xaxt = "n", yaxt = "n",
xlab="", ylab="", col = colors, zlim = zlim, ...)
abline(h=rows + 0.5, v = cols + 0.5)
axis(side = 1, cols, colnames(x), las = 2)
}
my_image(y)1. How would you describe the data based on this figure?
- The test scores are all independent of each other.
- The students that test well are at the top of the image and there seems to be three groupings by subject.
- The students that are good at math are not good at science.
- The students that are good at math are not good at humanities.
2. You can examine the correlation between the test scores directly like this:
Which of the following best describes what you see?
- The test scores are independent.
- Math and science are highly correlated, but the humanities are not.
- There is high correlation between tests in the same subject, but no correlation across subjects.
- There is a correlation among all tests, but higher if the tests are in science and math and even higher within each subject.
3. Remember that orthogonality means that \(U^{\top}U\) and \(V^{\top}V\) are equal to the identity matrix. This implies that we can also rewrite the decomposition as:
\[ \mathbf{Y V} = \mathbf{U D} \mbox{ or } \mathbf{U}^{\top}\mathbf{Y} = \mathbf{D V}^{\top}\]
We can think of \(\mathbf{YV}\) and \(\mathbf{U}^{\top}\mathbf{V}\) as two transformations of \(\mathbf{Y}\) that preserve the total variability.
Use the function svd to compute the SVD of y. This function will return \(U\), \(V\) and the diagonal entries of \(D\).
You can check that the SVD works by typing:
Compute the sum of squares of the columns of \(Y\) and store them in ss_y. Then compute the sum of squares of columns of the transformed \(\mathbf{YV}\) and store them in ss_yv. Confirm that sum(ss_y) is equal to sum(ss_yv).
4. We see that the total sum of squares is preserved. This is because \(\mathbf{V}\) is orthogonal. Now to start understanding how \(\mathbf{YV}\) is useful, plot ss_y against the column number and then do the same for ss_yv. What do you observe?
5. We see that the variability of the columns of \(\mathbf{YV}\) is decreasing. Furthermore, we see that, relative to the first three, the variability of the columns beyond the third is almost 0. Now notice that we didn’t have to compute ss_yv because we already have the answer. How? Remember that \(\mathbf{YV} = \mathbf{UD}\) and because \(\mathbf{U}\) is orthogonal, we know that the sum of squares of the columns of \(\mathbf{UD}\) are the diagonal entries of \(\mathbf{D}\) squared. Confirm this by plotting the square root of ss_yv versus the diagonal entries of \(\mathbf{D}\).
6. From the above we know that the sum of squares of the columns of \(\mathbf{Y}\) (the total sum of squares) add up to the sum of s$d^2, and that the transformation \(\mathbf{YV}\) gives us columns with sums of squares equal to s$d^2. Now compute what percent of the total variability is explained by just the first three columns of \(\mathbf{YV}\).
7. We see that almost 99% of the variability is explained by the first three columns of \(\mathbf{YV} = \mathbf{UD}\). So we get the sense that we should be able to explain much of the variability and structure we found while exploring the data with a few columns. Before we continue, let’s show a useful computational trick to avoid creating the matrix diag(s$d). To motivate this, we note that if we write \(\mathbf{U}\) out in its columns \([\mathbf{u}_1, \mathbf{u}_2, \dots, \mathbf{u}_p]\), then \(\mathbf{UD}\) is equal to:
\[ \mathbf{UD} = [\mathbf{u}_1 d_{1,1}, \mathbf{u}_2 d_{2,2}, \dots, \mathbf{u}_p d_{p,p}] \]
Use the sweep function to compute \(UD\) without constructing diag(s$d) and without using matrix multiplication.
8. We know that \(\mathbf{u}_1 d_{1,1}\), the first column of \(\mathbf{UD}\), has the most variability of all the columns of \(\mathbf{UD}\). Earlier we saw an image of \(Y\):
my_image(y)in which we can see that the student to student variability is quite large and that it appears that students that are good in one subject are good in all. This implies that the average (across all subjects) for each student should explain a lot of the variability. Compute the average score for each student and plot it against \(\mathbf{u}_1 d_{1,1}\), and describe what you find.
9. We note that the signs in SVD are arbitrary because:
\[ \mathbf{U D V}^{\top} = (-\mathbf{U}) D (-\mathbf{V})^{\top} \]
With this in mind, we see that the first column of \(\mathbf{UD}\) is almost identical to the average score for each student except for the sign.
This implies that multiplying \(\mathbf{Y}\) by the first column of \(\mathbf{V}\) must be performing a similar operation to taking the average. Make an image plot of \(\mathbf{V}\) and describe the first column relative to others and how this relates to taking an average.
10. We already saw that we can rewrite \(UD\) as:
\[ \mathbf{u}_1 d_{1,1} + \mathbf{u}_2 d_{2,2} + \dots + \mathbf{u}_p d_{p,p} \]
with \(\mathbf{u}_j\) the j-th column of \(\mathbf{U}\). This implies that we can rewrite the entire SVD as:
\[\mathbf{Y} = \mathbf{u}_1 d_{1,1} \mathbf{v}_1 ^{\top} + \mathbf{u}_2 d_{2,2} \mathbf{v}_2 ^{\top} + \dots + \mathbf{u}_p d_{p,p} \mathbf{v}_p ^{\top}\]
with \(\mathbf{V}_j\) the jth column of \(\mathbf{V}\). Plot \(\mathbf{u}_1\), then plot \(\mathbf{v}_1^{\top}\) using the same range for the y-axis limits. Then make an image of \(\mathbf{u}_1 d_{1,1} \mathbf{v}_1 ^{\top}\) and compare it to the image of \(\mathbf{Y}\). Hint: Use the my_image function defined above and use the drop=FALSE argument to assure the subsets of matrices are matrices.
11. We see that with just a vector of length 100, a scalar, and a vector of length 24, we actually come close to reconstructing the original \(100 \times 24\) matrix. This is our first matrix factorization:
\[
\mathbf{Y} \approx d_{1,1} \mathbf{u}_1 \mathbf{v}_1^{\top}
\] We know it explains s$d[1]^2/sum(s$d^2) * 100 percent of the total variability. Our approximation only explains the observation that good students tend to be good in all subjects. But another aspect of the original data that our approximation does not explain was the higher similarity we observed within subjects. We can see this by computing the difference between our approximation and original data and then computing the correlations. You can see this by running this code:
Now that we have removed the overall student effect, the correlation plot reveals that we have not yet explained the within subject correlation nor the fact that math and science are closer to each other than to the arts. So let’s explore the second column of the SVD. Repeat the previous exercise but for the second column: Plot \(\mathbf{u}_2\), then plot \(\mathbf{v}_2^{\top}\) using the same range for the y-axis limits, then make an image of \(\mathbf{u}_2 d_{2,2} \mathbf{v}_2 ^{\top}\) and compare it to the image of resid.
12. The second column clearly relates to a student’s difference in ability in math/science versus the arts. We can see this most clearly from the plot of s$v[,2]. Adding the matrix we obtain with these two columns will help with our approximation:
\[ \mathbf{Y} \approx d_{1,1} \mathbf{u}_1 \mathbf{v}_1^{\top} + d_{2,2} \mathbf{u}_2 \mathbf{v}_2^{\top} \]
We know it will explain:
percent of the total variability. We can compute new residuals like this:
and see that the structure that is left is driven by the differences between math and science. Confirm this by plotting \(\mathbf{u}_3\), then plot \(\mathbf{v}_3^{\top}\) using the same range for the y-axis limits, then make an image of \(\mathbf{u}_3 d_{3,3} \mathbf{v}_3 ^{\top}\) and compare it to the image of resid.
13. The third column clearly relates to a student’s difference in ability in math and science. We can see this most clearly from the plot of s$v[,3]. Adding the matrix we obtain with these two columns will help with our approximation:
\[ \mathbf{Y} \approx d_{1,1} \mathbf{u}_1 \mathbf{v}_1^{\top} + d_{2,2} \mathbf{u}_2 \mathbf{v}_2^{\top} + d_{3,3} \mathbf{u}_3 \mathbf{v}_3^{\top} \]
We know it will explain:
percent of the total variability. We can compute new residuals like this:
We no longer see structure in the residuals: they seem to be independent of each other. This implies that we can describe the data with the following model:
\[ \mathbf{Y} = \mathbf{u}_1 \mathbf{v}_1^{\top} + d_{2,2} \mathbf{u}_2 \mathbf{v}_2^{\top} + d_{3,3} \mathbf{u}_3 \mathbf{v}_3^{\top} + \varepsilon \]
with \(\varepsilon\) a matrix of independent identically distributed errors. This model is useful because we summarize \(100 \times 24\) observations with \(3 \times (100+24+1) = 375\) numbers. Furthermore, the three components of the model have useful interpretations: 1) the overall ability of a student, 2) the difference in ability between the math/sciences and arts, and 3) the remaining differences between the three subjects. The sizes \(d_{1,1}, d_{2,2}\) and \(d_{3,3}\) tell us the variability explained by each component. Finally, note that the components \(d_{j,j} \mathbf{u}_j \mathbf{v}_j^{\top}\) are equivalent to the jth principal component.
Finish the exercise by plotting an image of \(Y\), an image of \(d_{1,1} \mathbf{u}_1 \mathbf{v}_1^{\top} + d_{2,2} \mathbf{u}_2 \mathbf{v}_2^{\top} + d_{3,3} \mathbf{u}_3 \mathbf{v}_3^{\top}\) and an image of the residuals, all with the same zlim.