Capítulo 11 Resumos robustos
11.1 Valores atípicos
Anteriormente, descrevemos como os boxplots mostram outliers, mas não oferecemos uma definição precisa. Aqui discutimos discrepâncias, abordagens que podem ajudar a detectá-las e resumos que levam sua presença em consideração.
Os valores discrepantes são muito comuns na ciência de dados. A coleta de dados pode ser complexa e é comum observar pontos de dados gerados com erro. Por exemplo, um dispositivo de monitoramento antigo pode ler medições sem sentido antes de falhar completamente. O erro humano também é uma fonte de outliers, principalmente quando a entrada de dados é feita manualmente. Um indivíduo, por exemplo, pode digitar erroneamente sua altura em centímetros em vez de polegadas ou colocar o decimal no lugar errado.
Como distinguimos um outlier de medições que são muito grandes ou muito pequenas simplesmente por causa da variabilidade esperada? Nem sempre é uma pergunta fácil de responder, mas tentaremos oferecer algumas orientações. Vamos começar com um caso simples.
Suponha que um colega seja responsável por coletar dados demográficos para um grupo de homens. Os dados indicam a altura em pés e são armazenados no objeto:
library(tidyverse)
library(dslabs)
data(outlier_example)
str(outlier_example)
#> num [1:500] 5.59 5.8 5.54 6.15 5.83 5.54 5.87 5.93 5.89 5.67 ...Nosso colega usa o fato de que as alturas geralmente são bem aproximadas por uma distribuição normal e resume os dados com a média e o desvio padrão:
mean(outlier_example)
#> [1] 6.1
sd(outlier_example)
#> [1] 7.8e escreva um relatório sobre o fato interessante de que esse grupo de meninos é muito mais alto que o normal. A altura média é superior a seis pés! No entanto, usando seus conhecimentos de ciência de dados, eles percebem algo inesperado: o desvio padrão é superior a 7 pés. Ao somar e subtrair dois desvios padrão, eles observam que 95% dessa população parece ter alturas entre -9.489, 21.697 pés, isso não faz sentido. Um gráfico rápido mostra o problema:
boxplot(outlier_example)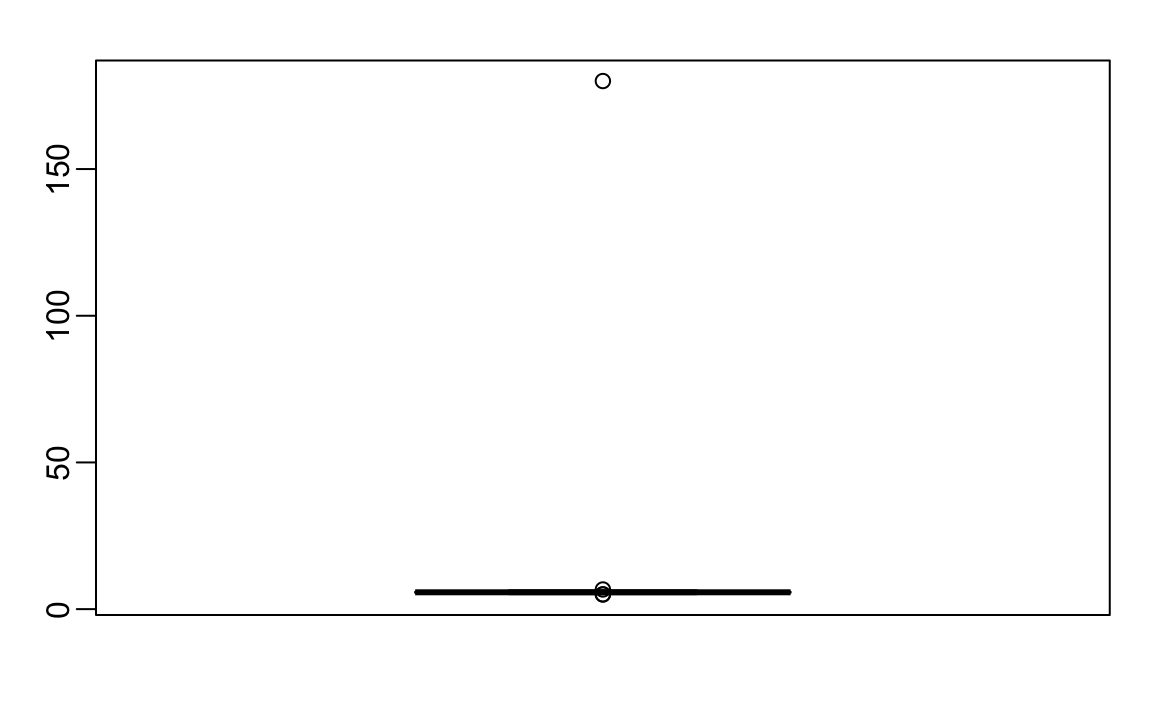
Parece haver pelo menos um valor que não faz sentido, pois sabemos que uma altura de 180 pés é impossível. O gráfico da caixa detecta esse ponto como um erro externo.
11.2 Mediana
Quando temos um erro externo como esse, a média pode ser muito grande. Matematicamente, podemos tornar a média tão grande quanto queremos simplesmente mudando um número: com 500 pontos de dados, podemos aumentar a média em qualquer quantidade \(\Delta\) adicionando \(\Delta \times\) NA para um único número. A mediana, definida como o valor pelo qual metade dos valores é menor e a outra metade é maior, é robusta para esses valores extremos. Por maior que seja o ponto maior, a mediana permanece a mesma.
Com esses dados, a mediana é:
median(outlier_example)
#> [1] 5.74que é sobre 5 pés e 9 polegadas.
A mediana é o que os gráficos da caixa mostram como uma linha horizontal.
11.3 O intervalo interquartil (IQR)
A caixa em um gráfico de caixa é definida pelo primeiro e terceiro quartis. Estes têm como objetivo fornecer uma idéia da variabilidade nos dados: 50% dos dados estão dentro desse intervalo. A diferença entre o terceiro e o primeiro quartil (ou os percentis 75 e 25) é conhecida como intervalo interquartil, ou IQR. Assim como a mediana, essa quantidade será robusta para valores discrepantes, uma vez que valores grandes não a afetam. Podemos fazer alguns cálculos e observar que, para os dados que seguem a distribuição normal, o IQR/ 1.349 se aproxima do desvio padrão dos dados se um erro externo não estiver presente. Podemos ver que isso funciona bem em nosso exemplo, pois obtemos uma estimativa do desvio padrão de:
IQR(outlier_example)/ 1.349
#> [1] 0.245que fica perto de 3 polegadas.
11.4 Definição de Tukey de um outlier
Em R, os pontos que ficam fora dos bigodes do box plot são chamados de outliers, uma definição que Tukey introduziu. O bigode superior termina no 75º percentil mais 1,5 \(\times\) IQR, enquanto o bigode inferior termina no 25º percentil menos 1,5 \(\times\) IQR. Se definirmos o primeiro e o terceiro quartis como \(Q_1\) e \(Q_3\), respectivamente, um valor externo é qualquer valor fora do intervalo:
\[[Q_1 - 1.5 \times (Q_3 - Q1), Q_3 + 1.5 \times (Q_3 - Q1)].\]
Quando os dados são normalmente distribuídos, as unidades padrão desses valores são:
q3 <- qnorm(0.75)
q1 <- qnorm(0.25)
iqr <- q3 - q1
r <- c(q1 - 1.5*iqr, q3 + 1.5*iqr)
r
#> [1] -2.7 2.7Usando a função pnorm, nós vemos que 99.3% de dados cai nesse intervalo.
Observe que este não é um evento tão extremo: se tivermos 1000 pontos de dados normalmente distribuídos, esperamos ver cerca de 7 fora desse intervalo. Mas estes não seriam discrepantes, como esperamos vê-los sob variação típica.
Se queremos que um outlier seja mais estranho, podemos mudar 1,5 para um número maior. Tukey também usou 3 e os chamou de outliers extremos_ ou outliers extremos. Com uma distribuição normal,
100%
dos dados cai nesse intervalo. Isso se traduz em cerca de 2 em um milhão de chances de estar fora de alcance. Na função geom_boxplot, isso pode ser controlado usando o argumento outlier.size, que por padrão é 1,5.
A medição de 180 polegadas está além da faixa dos dados de altura:
max_height <- quantile(outlier_example, 0.75) + 3*IQR(outlier_example)
max_height
#> 75%
#> 6.91Se removermos esse valor, podemos ver que os dados são normalmente distribuídos conforme o esperado:
x <- outlier_example[outlier_example < max_height]
qqnorm(x)
qqline(x)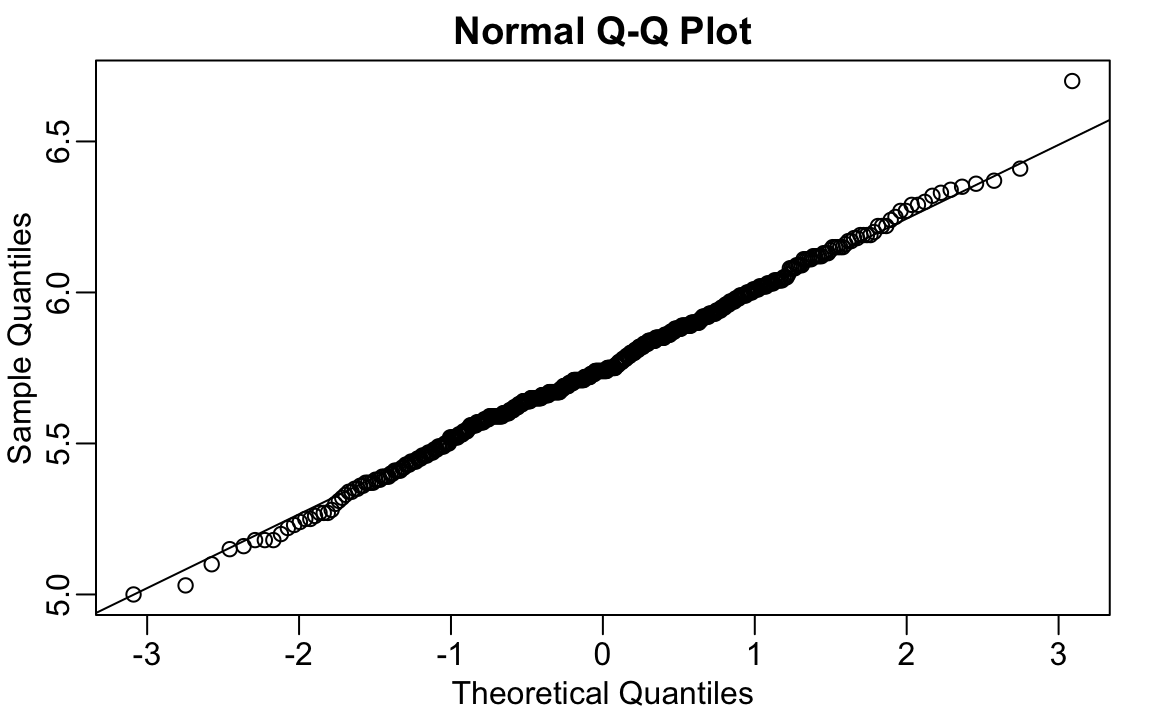
11.5 Desvio absoluto mediano
Outra opção para estimar o desvio padrão de maneira robusta na presença de outliers é usar o desvio absoluto médio, ou MAD. Para calcular o MAD, primeiro calculamos a mediana e, em seguida, para cada valor, calculamos a distância entre esse valor e a mediana. MAD é definido como a mediana dessas distâncias. Por razões técnicas não discutidas aqui, esse valor deve ser multiplicado por 1,4826 para garantir que ele se aproxime do desvio padrão real. A função mad já incorpora essa correção. Para os dados de altura, obtemos um MAD de:
mad(outlier_example)
#> [1] 0.237que fica perto de 3 polegadas.
11.6 Exercícios
Nós vamos usar o pacote HistData. Se você não o instalou, pode fazê-lo assim:
install.packages("HistData")Carregue o conjunto de dados de altura e crie um vetor x ele contém apenas as alturas masculinas dos dados de Galton sobre pais e filhos de suas pesquisas históricas sobre herança.
library(HistData)
data(Galton)
x <- Galton$child1. Calcule a média e a mediana desses dados.
2. Calcule a mediana e o MAD desses dados.
3. Agora, suponha que Galton tenha cometido um erro ao inserir o primeiro valor e esqueceu de usar o ponto decimal. Você pode imitar esse erro digitando:
x_with_error <- x
x_with_error[1] <- x_with_error[1]*10Quantas polegadas a média cresce como resultado desse erro?
4. Quantas polegadas o SD cresce como resultado desse erro?
5. Quantas polegadas a mediana cresce como resultado desse erro?
6. Quantas polegadas o MAD cresce como resultado desse erro?
7. Como poderíamos usar a análise exploratória de dados para detectar que um erro foi cometido?
para. Como é apenas um valor entre muitos, isso não pode ser detectado. b. Veríamos uma mudança óbvia na distribuição. c. Um gráfico de caixa, histograma ou QQ revelaria um erro óbvio. d. Um diagrama de dispersão mostraria altos níveis de erro de medição.
8. Quanto a média pode crescer acidentalmente com erros como esse? Escreva uma função chamada error_avg que leva um valor k e retorna a média do vetor x após a primeira entrada mudar para k. Mostrar resultados para k=10000 e k=-10000.
11.7 Estudo de caso: altura do aluno autorreferida
As alturas que estudamos não são as alturas originais relatadas pelos alunos. As alturas originais também estão incluídas no pacote dslabs e podem ser carregadas assim:
library(dslabs)
data("reported_heights")Height é um vetor de caracteres, por isso criamos uma nova coluna com a versão numérica:
reported_heights <- reported_heights %>%
mutate(original_heights = height, height = as.numeric(height))
#> Warning: Problem with `mutate()` input `height`.
#> ℹ NAs introduced by coercion
#> ℹ Input `height` is `as.numeric(height)`.
#> Warning in mask$eval_all_mutate(dots[[i]]): NAs introduced by coercionObserve que recebemos um aviso sobre NAs. Isso ocorre porque algumas das alturas autorreferidas não eram números. Podemos ver por que temos essas NAs:
reported_heights %>% filter(is.na(height)) %>% head()
#> time_stamp sex height original_heights
#> 1 2014-09-02 15:16:28 Male NA 5' 4"
#> 2 2014-09-02 15:16:37 Female NA 165cm
#> 3 2014-09-02 15:16:52 Male NA 5'7
#> 4 2014-09-02 15:16:56 Male NA >9000
#> 5 2014-09-02 15:16:56 Male NA 5'7"
#> 6 2014-09-02 15:17:09 Female NA 5'3"Alguns alunos relataram suas alturas usando pés e polegadas em vez de apenas polegadas. Outros usavam centímetros e outros estavam apenas trollando. Por enquanto, removeremos essas entradas:
reported_heights <- filter(reported_heights, !is.na(height))Se calcularmos a média e o desvio padrão, observamos que obtemos resultados estranhos. A média e o desvio padrão são diferentes da mediana e do MAD:
reported_heights %>%
group_by(sex) %>%
summarize(average = mean(height), sd = sd(height),
median = median(height), MAD = mad(height))
#> `summarise()` ungrouping output (override with `.groups` argument)
#> # A tibble: 2 x 5
#> sex average sd median MAD
#> <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 Female 63.4 27.9 64.2 4.05
#> 2 Male 103. 530. 70 4.45Isso sugere que temos discrepâncias, o que é confirmado pela criação de um gráfico de caixa:
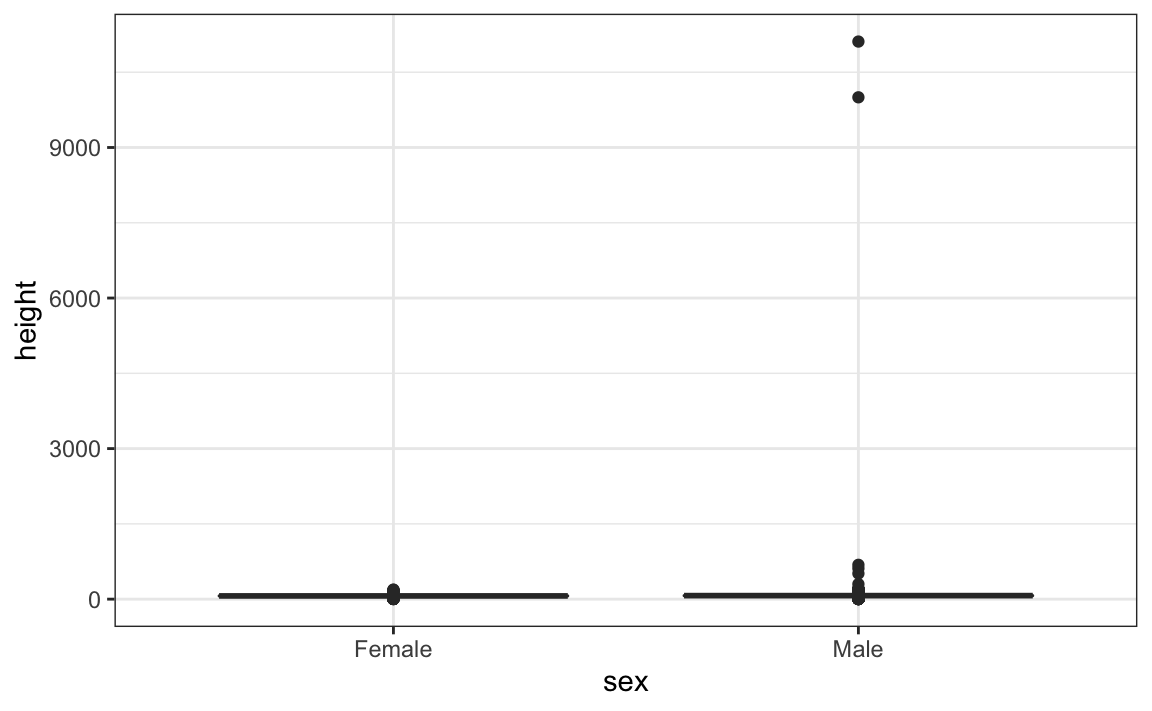
Vemos alguns valores extremos. Para ver quais são esses valores, podemos analisar rapidamente os valores maiores usando a função arrange:
reported_heights %>% arrange(desc(height)) %>% top_n(10, height)
#> time_stamp sex height original_heights
#> 1 2014-09-03 23:55:37 Male 11111 11111
#> 2 2016-04-10 22:45:49 Male 10000 10000
#> 3 2015-08-10 03:10:01 Male 684 684
#> 4 2015-02-27 18:05:06 Male 612 612
#> 5 2014-09-02 15:16:41 Male 511 511
#> 6 2014-09-07 20:53:43 Male 300 300
#> 7 2014-11-28 12:18:40 Male 214 214
#> 8 2017-04-03 16:16:57 Male 210 210
#> 9 2015-11-24 10:39:45 Male 192 192
#> 10 2014-12-26 10:00:12 Male 190 190
#> 11 2016-11-06 10:21:02 Female 190 190As primeiras sete entradas parecem erros estranhos. No entanto, as seguintes entradas parecem ter sido inseridas em centímetros em vez de polegadas. Como 184 cm equivale a seis pés de altura, suspeitamos que 184 signifique 72 polegadas.
Podemos revisar todas as respostas sem sentido examinando os dados que Tukey considera far out_ou_extremos:
whisker <- 3*IQR(reported_heights$height)
max_height <- quantile(reported_heights$height, .75) + whisker
min_height <- quantile(reported_heights$height, .25) - whisker
reported_heights %>%
filter(!between(height, min_height, max_height)) %>%
select(original_heights) %>%
head(n=10) %>% pull(original_heights)
#> [1] "6" "5.3" "511" "6" "2" "5.25" "5.5" "11111"
#> [9] "6" "6.5"Verificando cuidadosamente essas alturas, vemos dois erros comuns: entradas em centímetros, que se tornam muito grandes, e entradas do tipo x.y com x e y representando pés e polegadas, respectivamente, que acabam sendo muito pequenos. Alguns dos valores ainda menores, como 1.6, podem ser entradas em metros.
Na parte data wrangling deste livro, aprenderemos técnicas para corrigir esses valores e convertê-los em polegadas. Aqui, conseguimos detectar esse problema explorando cuidadosamente os dados para descobrir problemas com eles - o primeiro passo na grande maioria dos projetos de ciência de dados.