Capítulo 3 Conceptos básicos de programación

3.1 Expresiones condicionales

Las expresiones condicionales son una de las características básicas de la programación. Se utilizan para lo que se denomina flow control. La expresión condicional más común es la declaración if-else. En R, podemos realizar mucho análisis de datos sin condicionales. Sin embargo, aparecen ocasionalmente y los necesitarán una vez comiencen a escribir sus propias funciones y paquetes.

Aquí presentamos un ejemplo muy sencillo que muestra la estructura general de una instrucción if-else. La idea básica es imprimir el recíproco de a a menos que a sea 0:

a <- 0

if(a!=0){
  print(1/a)
} else{
  print("No reciprocal for 0.")
}
#> [1] "No reciprocal for 0."

Veamos otro ejemplo usando el set de datos de asesinatos de EE. UU.:

library(dslabs)
data(murders)
murder_rate <- murders$total/ murders$population*100000

Aquí ofrecemos un ejemplo muy sencillo que nos dice qué estados, si los hay, tienen una tasa de homicidios inferior a 0.5 por 100,000. Las declaraciones if nos protegen del caso en el que ningún estado satisface la condición.

ind <- which.min(murder_rate)

if(murder_rate[ind] < 0.5){
  print(murders$state[ind])
} else{
  print("No state has murder rate that low")
}
#> [1] "Vermont"

Si lo intentamos nuevamente con una tasa de 0.25, obtenemos una respuesta diferente:

if(murder_rate[ind] < 0.25){
  print(murders$state[ind])
} else{
  print("No state has a murder rate that low.")
}
#> [1] "No state has a murder rate that low."

Una función relacionada que es muy útil es ifelse. Esta función toma tres argumentos: un lógico y dos posibles respuestas. Si el lógico es TRUE, devuelve el valor en el segundo argumento y, si es FALSE, devuelve el valor en el tercer argumento. Aquí tenemos un ejemplo:

a <- 0
ifelse(a > 0, 1/a, NA)
#> [1] NA

Esta función es particularmente útil porque sirve para vectores. Examina cada entrada del vector lógico y devuelve elementos del vector proporcionado en el segundo argumento, si la entrada es TRUE, o elementos del vector proporcionado en el tercer argumento, si la entrada es FALSE.

a <- c(0, 1, 2, -4, 5)
result <- ifelse(a > 0, 1/a, NA)

Esta tabla nos ayuda a ver qué sucedió:

a	is_a_positive	answer1	answer2	result
0	FALSE	Inf	NA	NA
1	TRUE	1.00	NA	1.0
2	TRUE	0.50	NA	0.5
-4	FALSE	-0.25	NA	NA
5	TRUE	0.20	NA	0.2

Aquí hay un ejemplo de cómo esta función se puede usar fácilmente para reemplazar todos los valores faltantes en un vector con ceros:

data(na_example)
no_nas <- ifelse(is.na(na_example), 0, na_example)
sum(is.na(no_nas))
#> [1] 0

Otras dos funciones útiles son any y all. La función any toma un vector de lógicos y devuelve TRUE si alguna de las entradas es TRUE. La función all toma un vector de lógicos y devuelve TRUE si todas las entradas son TRUE. Aquí ofrecemos un ejemplo:

z <- c(TRUE, TRUE, FALSE)
any(z)
#> [1] TRUE
all(z)
#> [1] FALSE

3.2 Cómo definir funciones

A medida que adquieran más experiencia, necesitarán realizar las mismas operaciones una y otra vez. Un ejemplo sencillo es el cálculo de promedios. Podemos calcular el promedio de un vector x utilizando las funciones sum y length: sum(x)/length(x). Debido a que hacemos esto repetidas veces, es mucho más eficiente escribir una función que realice esta operación. Esta operación particular es tan común que alguien ya escribió la función mean y se incluye en la base R. Sin embargo, se encontrarán con situaciones en las que la función aún no existe, por lo que R les permite escribir una. Se puede definir una versión sencilla de una función que calcula el promedio así:

avg <- function(x){
  s <- sum(x)
  n <- length(x)
  s/n
}

Ahora avg es una función que calcula el promedio:

x <- 1:100
identical(mean(x), avg(x))
#> [1] TRUE

Observen que las variables definidas dentro de una función no se guardan en el espacio de trabajo. Por lo tanto, mientras usamos s y n cuando llamamos (call en inglés) avg, los valores se crean y cambian solo durante la llamada. Aquí podemos ver un ejemplo ilustrativo:

s <- 3
avg(1:10)
#> [1] 5.5
s
#> [1] 3

Noten como s todavía es 3 después de que llamamos avg.

En general, las funciones son objetos, por lo que les asignamos nombres de variables con <-. La función function le dice a R que están a punto de definir una función. La forma general de la definición de una función es así:

my_function <- function(VARIABLE_NAME){
  perform operations on VARIABLE_NAME and calculate VALUE
  VALUE
}

Las funciones que definen pueden tener múltiples argumentos, así como valores predeterminados. Por ejemplo, podemos definir una función que calcule el promedio aritmético o geométrico dependiendo de una variable definida por usuarios como esta:

avg <- function(x, arithmetic = TRUE){
  n <- length(x)
  ifelse(arithmetic, sum(x)/n, prod(x)^(1/n))
}

Aprenderemos más sobre cómo crear funciones a través de la experiencia a medida que nos enfrentemos a tareas más complejas.

3.3 Namespaces

Una vez que comiencen a convertirse en usuarios expertos de R, es probable que necesiten cargar varios complementos de paquetes (add-ons en inglés) para algunos de sus análisis. Tan pronto hagan eso, es probable que descubran que dos paquetes a veces usan el mismo nombre para dos funciones diferentes. Y a menudo estas funciones hacen cosas completamente diferentes. De hecho, ya hemos visto esto porque ambos paquetes de base R dplyr y stats definen una función filter. Hay otros cinco ejemplos en dplyr. Sabemos esto porque cuando cargamos dplyr por primera vez, vemos el siguiente mensaje:

The following objects are masked from ‘package:stats’:

filter, lag

The following objects are masked from ‘package:base’:

intersect, setdiff, setequal, union

Entonces, ¿qué hace R cuando escribimos filter? ¿Utiliza la función dplyr o la función stats? De nuestro trabajo anterior sabemos que usa dplyr. Pero, ¿qué pasa si queremos usar stats?

Estas funciones viven en diferentes namespaces. R seguirá un cierto orden cuando busque una función en estos namespaces. Pueden ver el orden escribiendo:

search()

La primera entrada en esta lista es el ambiente global que incluye todos los objetos que definen.

Entonces, ¿qué pasa si queremos usar el filter stats en lugar del filter dplyr pero dplyr aparece primero en la lista de búsqueda? Pueden forzar el uso de un namespace específico utilizando dos puntos dobles ( ::) así:

stats::filter

Si queremos estar absolutamente seguros de que usamos el filter de dplyr, podemos usar:

dplyr::filter

Recuerden que si queremos usar una función en un paquete sin cargar el paquete completo, también podemos usar los dos puntos dobles.

Para más información sobre este tema más avanzado, recomendamos el libro de paquetes R¹⁵.

3.4 Bucles-for

La fórmula para la suma de la serie \(1+2+\dots+n\) es \(n(n+1)/2\). ¿Qué pasaría si no estuviéramos seguros de que esa era la función correcta? ¿Cómo podríamos verificar? Usando lo que aprendimos sobre las funciones, podemos crear una que calcule \(S_n\):

compute_s_n <- function(n){
  x <- 1:n
  sum(x)
}

¿Cómo podemos calcular \(S_n\) para varios valores de \(n\), digamos \(n=1,\dots,25\)? ¿Escribimos 25 líneas de código llamando compute_s_n? No. Para eso están los bucles-for (for-loops en inglés) en la programación. En este caso, estamos realizando exactamente la misma tarea una y otra vez, y lo único que está cambiando es el valor de \(n\). Los bucles-for nos permiten definir el rango que toma nuestra variable (en nuestro ejemplo \(n=1,\dots,10\)), luego cambiar el valor y evaluar la expresión a medida que realice un bucle.

Quizás el ejemplo más sencillo de un bucle-for es este código inútil:

for(i in 1:5){
  print(i)
}
#> [1] 1
#> [1] 2
#> [1] 3
#> [1] 4
#> [1] 5

Aquí está el bucle-for que escribiríamos para nuestro ejemplo \(S_n\):

m <- 25
s_n <- vector(length = m) # create an empty vector
for(n in 1:m){
  s_n[n] <- compute_s_n(n)
}

En cada iteración \(n=1\), \(n=2\), etc …, calculamos \(S_n\) y lo guardamos en la entrada \(n\) de s_n.

Ahora podemos crear un gráfico para buscar un patrón:

n <- 1:m
plot(n, s_n)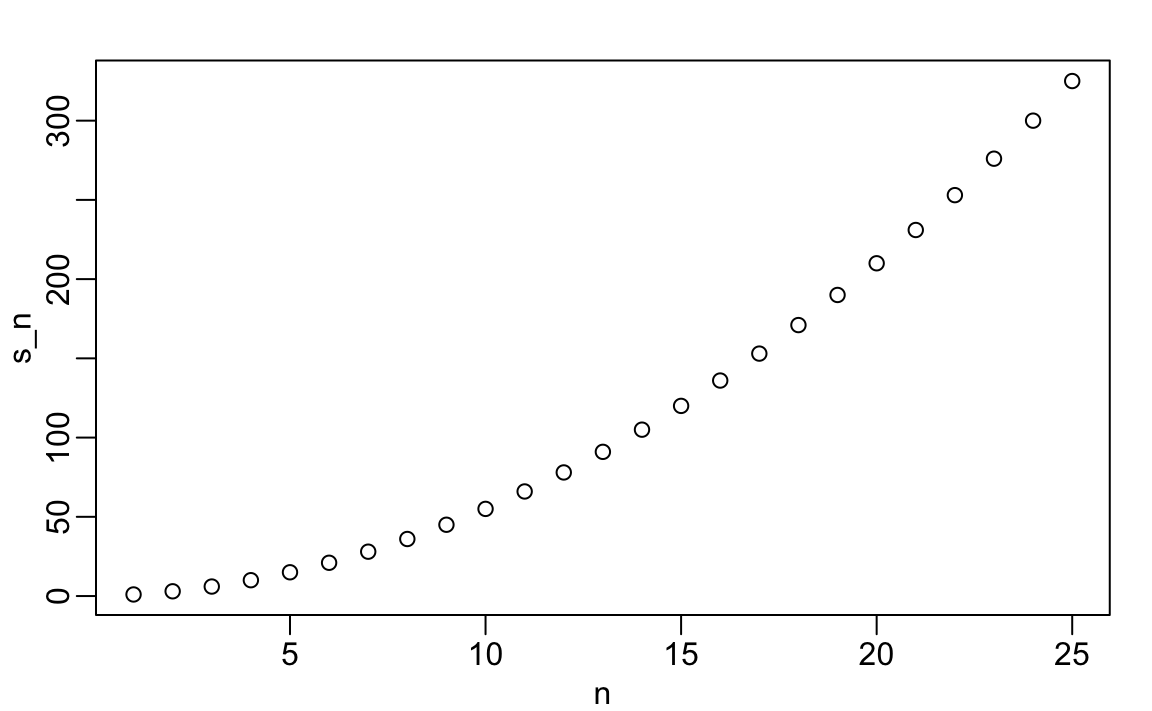

Si notaron que parece ser cuadrático, van por buen camino porque la fórmula es \(n(n+1)/2\).

3.5 Vectorización y funcionales

Aunque los bucles-for son un concepto importante para entender, no se usan mucho en R. A medida que aprendan más R, se darán cuenta de que la vectorización es preferible a los bucles-for puesto que resulta en un código más corto y claro. Ya vimos ejemplos en la sección de aritmética de vectores. Una función vectorizada es una función que aplicará la misma operación en cada uno de los vectores.

x <- 1:10
sqrt(x)
#>  [1] 1.00 1.41 1.73 2.00 2.24 2.45 2.65 2.83 3.00 3.16
y <- 1:10
x*y
#>  [1]   1   4   9  16  25  36  49  64  81 100

Para hacer este cálculo, no necesitamos los bucles-for. Sin embargo, no todas las funciones funcionan de esta manera. Por ejemplo, la función que acabamos de escribir, compute_s_n, no funciona elemento por elemento ya que espera un escalar. Este fragmento de código no ejecuta la función en cada entrada de n:

n <- 1:25
compute_s_n(n)

Los funcionales son funciones que nos ayudan a aplicar la misma función a cada entrada en un vector, matriz, data frame o lista. Aquí cubrimos el funcional que opera en vectores numéricos, lógicos y de caracteres: sapply.

La función sapply nos permite realizar operaciones basadas en elementos (element-wise en inglés) en cualquier función. Aquí podemos ver como funciona:

x <- 1:10
sapply(x, sqrt)
#>  [1] 1.00 1.41 1.73 2.00 2.24 2.45 2.65 2.83 3.00 3.16

Cada elemento de x se pasa a la función sqrt y devuelve el resultado. Estos resultados se concatenan. En este caso, el resultado es un vector de la misma longitud que el original, x. Esto implica que el bucle-for anterior puede escribirse de la siguiente manera:

n <- 1:25
s_n <- sapply(n, compute_s_n)

Otros funcionales son apply, lapply, tapply, mapply, vapply y replicate. Usamos principalmente sapply, apply y replicate en este libro, pero recomendamos familiarizarse con los demás ya que pueden ser muy útiles.

3.6 Ejercicios

1. ¿Qué devolverá esta expresión condicional?

x <- c(1,2,-3,4)

if(all(x>0)){
  print("All Postives")
} else{
  print("Not all positives")
}

2. ¿Cuál de las siguientes expresiones es siempre FALSE cuando al menos una entrada de un vector lógico x es TRUE?

1. all(x)
2. any(x)
3. any(!x)
4. all(!x)

3. La función nchar le dice cuántos caracteres tiene un vector de caracteres. Escriba una línea de código que le asigne al objeto new_names la abreviatura del estado cuando el nombre del estado tiene más de 8 caracteres.

4. Cree una función sum_n que para cualquier valor dado, digamos \(n\), calcula la suma de los enteros de 1 a n (inclusivo). Use la función para determinar la suma de los enteros de 1 a 5,000.

5. Cree una función altman_plot que toma dos argumentos, x y y, y grafica la diferencia contra la suma.

6. Después de ejecutar el siguiente código, ¿cuál es el valor de x?

x <- 3
my_func <- function(y){
  x <- 5
  y+5
}

7. Escriba una función compute_s_n que para cualquier \(n\) calcula la suma \(S_n = 1^2 + 2^2 + 3^2 + \dots n^2\). Indique el valor de la suma cuando \(n=10\).

8. Defina un vector numérico vacío s_n de tamaño 25 usando s_n <- vector("numeric", 25) y almacene los resultados de \(S_1, S_2, \dots S_{25}\) usando un bucle-for.

9. Repita el ejercicio 8, pero esta vez use sapply.

10. Repita el ejercicio 8, pero esta vez use map_dbl.

11. Grafique \(S_n\) versus \(n\). Use puntos definidos por \(n=1,\dots,25\).

12. Confirme que la fórmula para esta suma es \(S_n= n(n+1)(2n+1)/6\).

---

15. http://r-pkgs.had.co.nz/namespace.html↩︎