Capítulo 32 Machine learning en la práctica
Ahora que hemos aprendido varios métodos y los hemos explorado con ejemplos ilustrativos, los aplicaremos a un ejemplo real: los dígitos MNIST.
Podemos cargar estos datos usando el siguiente paquete de dslabs:
library(tidyverse)
library(dslabs)
mnist <- read_mnist()El set de datos incluye dos componentes, un set de entrenamiento y un set de evaluación:
names(mnist)
#> [1] "train" "test"Cada uno de estos componentes incluye una matriz con atributos en las columnas:
dim(mnist$train$images)
#> [1] 60000 784y un vector con las clases como enteros:
class(mnist$train$labels)
#> [1] "integer"
table(mnist$train$labels)
#>
#> 0 1 2 3 4 5 6 7 8 9
#> 5923 6742 5958 6131 5842 5421 5918 6265 5851 5949Como queremos que este ejemplo se ejecute en una computadora portátil pequeña y en menos de una hora, consideraremos un subconjunto del set de datos. Tomaremos muestras de 10,000 filas aleatorias del set de entrenamiento y 1,000 filas aleatorias del set de evaluación:
set.seed(1990)
index <- sample(nrow(mnist$train$images), 10000)
x <- mnist$train$images[index,]
y <- factor(mnist$train$labels[index])
index <- sample(nrow(mnist$test$images), 1000)
x_test <- mnist$test$images[index,]
y_test <- factor(mnist$test$labels[index])32.1 Preprocesamiento
En machine learning, a menudo transformamos predictores antes de ejecutar el algoritmo. También eliminamos predictores que claramente no son útiles. Llamamos a estos pasos preprocesamiento (preprocessing en inglés).
Ejemplos de preprocesamiento incluyen estandarizar los predictores, transformar logarítmicamente algunos predictores, eliminar los predictores que están altamente correlacionados con otros y eliminar los predictores con muy pocos valores no únicos o una variación cercana a cero. Mostramos un ejemplo a continuación.
Podemos ejecutar la función nearZero del paquete caret para ver que muchos atributos no varían mucho de una observación a otra. Podemos ver que hay una gran cantidad de atributos con variabilidad 0:
library(matrixStats)
sds <- colSds(x)
qplot(sds, bins = 256)![]()
Esto se espera porque hay partes de la imagen que raras veces contienen escritura (píxeles oscuros).
El paquete caret incluye una función que recomienda que se eliminen estos atributos debido a que la variación es casi cero:
library(caret)
nzv <- nearZeroVar(x)Podemos ver las columnas que se recomiendan eliminar:
image(matrix(1:784 %in% nzv, 28, 28))rafalib::mypar()
image(matrix(1:784 %in% nzv, 28, 28))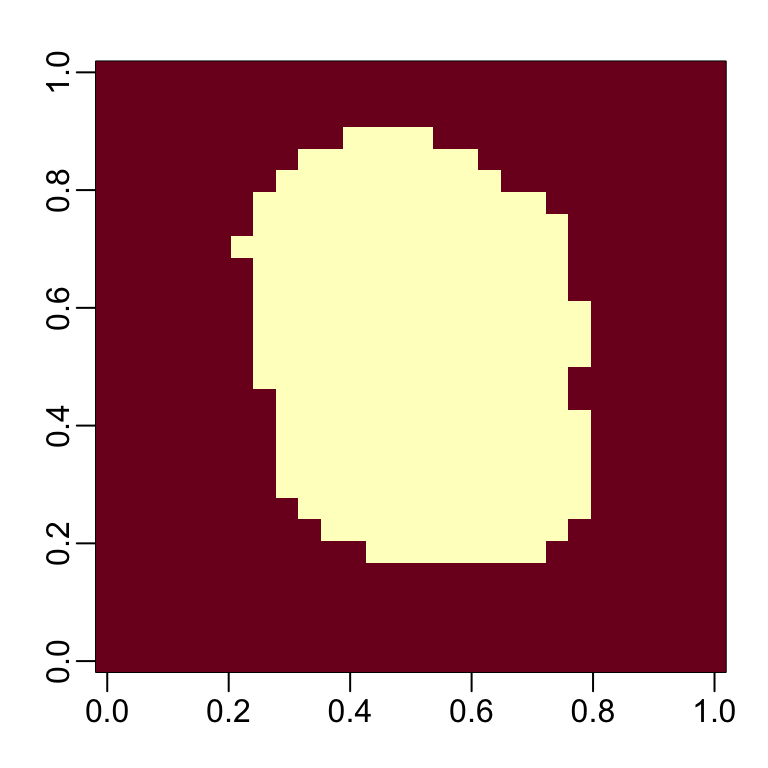
Entonces nos quedeamos con este número de columnas:
col_index <- setdiff(1:ncol(x), nzv)
length(col_index)
#> [1] 252Ahora estamos listos para adaptarnos a algunos modelos. Antes de comenzar, debemos agregar nombres de columna a las matrices de predictores, ya que caret los requiere:
colnames(x) <- 1:ncol(mnist$train$images)
colnames(x_test) <- colnames(x)32.2 k-vecino más cercano y bosque aleatorio
Comencemos con kNN. El primer paso es optimizar para \(k\). Tengan en cuenta que cuando ejecutamos el algoritmo, tendremos que calcular una distancia entre cada observación en el set de evaluación y cada observación en el set de entrenamiento. Hay muchos cálculos. Por lo tanto, utilizaremos la validación cruzada k-fold para mejorar la velocidad.
Si ejecutamos el siguiente código, el tiempo de computación en una computadora portátil estándar será de varios minutos.
control <- trainControl(method = "cv", number = 10, p = .9)
train_knn <- train(x[ ,col_index], y,
method = "knn",
tuneGrid = data.frame(k = c(3,5,7)),
trControl = control)
train_knnEn general, es una buena idea hacer una prueba con un subconjunto de datos para tener una idea del tiempo antes de comenzar a ejecutar un código que puede tardar horas en completarse. Podemos hacer esto de la siguiente manera:
n <- 1000
b <- 2
index <- sample(nrow(x), n)
control <- trainControl(method = "cv", number = b, p = .9)
train_knn <- train(x[index, col_index], y[index],
method = "knn",
tuneGrid = data.frame(k = c(3,5,7)),
trControl = control)Entonces podemos aumentar n y b e intentar establecer un patrón de cómo afectan el tiempo de computación para tener una idea de cuánto tiempo tomará el proceso de ajuste para valores mayores de n y b. Quieren saber si una función tomará horas, o incluso días, antes de ejecutarla.
Una vez que optimicemos nuestro algoritmo, podemos aplicarlo a todo el set de datos:
fit_knn <- knn3(x[, col_index], y, k = 3)¡La exactitud es casi 0.95!
y_hat_knn <- predict(fit_knn, x_test[, col_index], type="class")
cm <- confusionMatrix(y_hat_knn, factor(y_test))
cm$overall["Accuracy"]
#> Accuracy
#> 0.953Ahora logramos una exactitud de aproximadamente 0.95. De la especificidad y sensibilidad, también vemos que los 8 son los más difíciles de detectar y que el dígito pronosticado incorrectamente con mas frecuencia es el 7.
cm$byClass[,1:2]
#> Sensitivity Specificity
#> Class: 0 0.990 0.996
#> Class: 1 1.000 0.993
#> Class: 2 0.965 0.997
#> Class: 3 0.950 0.999
#> Class: 4 0.930 0.997
#> Class: 5 0.921 0.993
#> Class: 6 0.977 0.996
#> Class: 7 0.956 0.989
#> Class: 8 0.887 0.999
#> Class: 9 0.951 0.990Ahora veamos si podemos hacerlo aún mejor con el algoritmo de bosque aleatorio.
Con bosque aleatorio, el tiempo de cálculo es un reto. Para cada bosque, necesitamos construir cientos de árboles. También tenemos varios parámetros que podemos ajustar.
Debido a que con el bosque aleatorio el ajuste es la parte más lenta del procedimiento en lugar de la predicción (como con kNN), usaremos solo una validación cruzada de cinco pliegues (folds en inglés). Además, reduciremos la cantidad de árboles que se ajustan ya que aún no estamos construyendo nuestro modelo final.
Finalmente, para calcular en un set de datos más pequeño, tomaremos una muestra aleatoria de las observaciones al construir cada árbol. Podemos cambiar este número con el argumento nSamp.
library(randomForest)
control <- trainControl(method="cv", number = 5)
grid <- data.frame(mtry = c(1, 5, 10, 25, 50, 100))
train_rf <- train(x[, col_index], y,
method = "rf",
ntree = 150,
trControl = control,
tuneGrid = grid,
nSamp = 5000)Ahora que hemos optimizado nuestro algoritmo, estamos listos para ajustar nuestro modelo final:
fit_rf <- randomForest(x[, col_index], y,
minNode = train_rf$bestTune$mtry)Para verificar que ejecutamos suficientes árboles, podemos usar la función plot:
plot(fit_rf)Vemos que logramos una alta exactitud:
y_hat_rf <- predict(fit_rf, x_test[ ,col_index])
cm <- confusionMatrix(y_hat_rf, y_test)
cm$overall["Accuracy"]
#> Accuracy
#> 0.956Con algunos ajustes adicionales, podemos obtener una exactitud aún mayor.
32.3 Importancia variable
La siguiente función calcula la importancia de cada atributo:
imp <- importance(fit_rf)Podemos ver qué atributos se utilizan más al graficar una imagen:
mat <- rep(0, ncol(x))
mat[col_index] <- imp
image(matrix(mat, 28, 28))rafalib::mypar()
mat <- rep(0, ncol(x))
mat[col_index] <- imp
image(matrix(mat, 28, 28))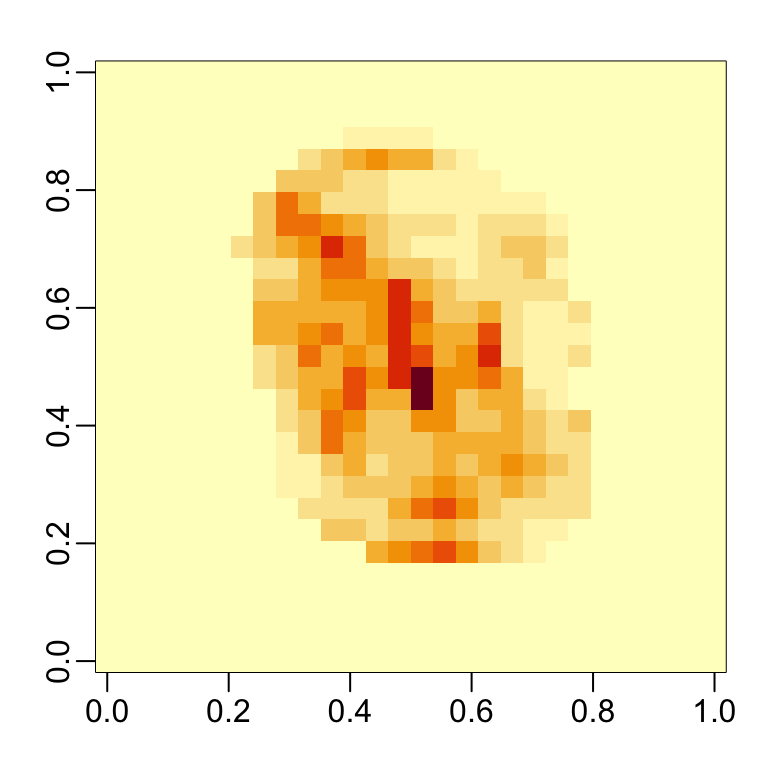
32.4 Evaluaciones visuales
Una parte importante del análisis de datos es visualizar los resultados para determinar por qué estamos fallando. Cómo hacemos esto depende de la aplicación. A continuación mostramos las imágenes de dígitos para los cuales hicimos una predicción incorrecta. Podemos comparar lo que obtenemos con kNN a los resultados de bosque aleatorio.
Aquí vemos unos errores para el bosque aleatorio:
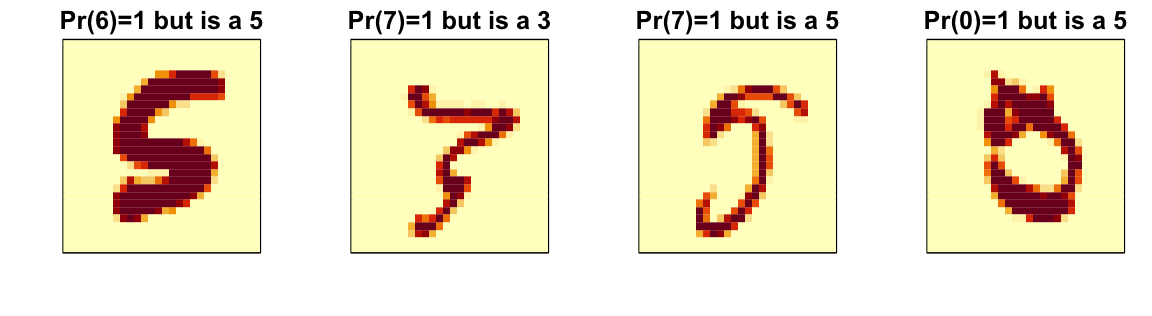
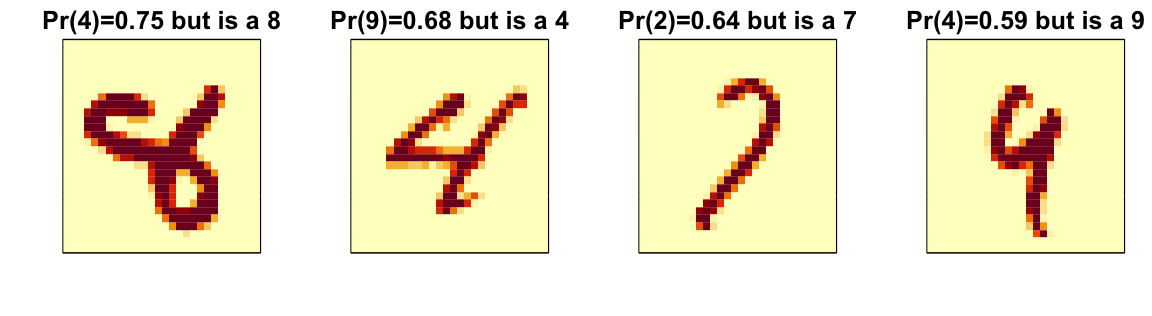
Al examinar errores como este, a menudo encontramos debilidades específicas en los algoritmos o en las opciones de parámetros que podemos intentar corregir.
32.5 Conjuntos
La idea de un conjunto (ensemble en inglés) es similar a la idea de combinar datos de diferentes encuestadores para obtener un mejor estimador del verdadero apoyo para cada candidato.
En machine learning, generalmente se pueden mejorar los resultados finales combinando los resultados de diferentes algoritmos.
Aquí hay un ejemplo sencillo donde calculamos nuevas probabilidades de clase tomando el promedio de bosque aleatorio y kNN. Podemos ver que la exactitud mejora a 0.96:
p_rf <- predict(fit_rf, x_test[,col_index], type = "prob")
p_rf<- p_rf/ rowSums(p_rf)
p_knn <- predict(fit_knn, x_test[,col_index])
p <- (p_rf + p_knn)/2
y_pred <- factor(apply(p, 1, which.max)-1)
confusionMatrix(y_pred, y_test)$overall["Accuracy"]
#> Accuracy
#> 0.961En los ejercicios, vamos a construir varios modelos de machine learning para el set de datos mnist_27 y luego construir un conjunto.
32.6 Ejercicios
1. Utilice el set de entrenamiento mnist_27 para construir un modelo con varios de los modelos disponibles del paquete caret. Por ejemplo, puede tratar estos:
models <- c("glm", "lda", "naive_bayes", "svmLinear", "gamboost",
"gamLoess", "qda", "knn", "kknn", "loclda", "gam", "rf",
"ranger","wsrf", "Rborist", "avNNet", "mlp", "monmlp", "gbm",
"adaboost", "svmRadial", "svmRadialCost", "svmRadialSigma")Aunque no hemos explicado muchos de estos algoritmos, aplíquelos usando train con todos los parámetros predeterminados. Guarde los resultados en una lista. Es posible que tenga que instalar algunos paquetes. Es posible que probablemente recibirá algunas advertencias.
2. Ahora que tiene todos los modelos entrenados en una lista, use sapply o map para crear una matriz de predicciones para el set de evaluación. Debería terminar con una matriz con length(mnist_27$test$y) filas y length(models) columnas.
3. Ahora calcule la exactitud para cada modelo en el set de evaluación.
4. Ahora construya una predicción de conjunto para el voto mayoritario y calcule su exactitud.
5. Anteriormente calculamos la exactitud de cada método en el set de entrenamiento y notamos que variaban. ¿Qué métodos individuales funcionan mejor que el conjunto?
6. Es tentador eliminar los métodos que no funcionan bien y volver a hacer el conjunto. El problema con este acercamiento es que estamos utilizando los datos de evaluación para tomar una decisión. Sin embargo, podríamos usar los estimadores de exactitud obtenidos de la validación cruzada con los datos de entrenamiento. Obtenga estos estimadores y guárdelos en un objeto.
7. Ahora solo consideremos los métodos con una exactitud estimada de 0.8 al construir el conjunto. ¿Cuál es la exactitud ahora?
8. Avanzado: Si dos métodos dan resultados que son iguales, unirlos no cambiará los resultados en absoluto. Para cada par de métricas, compare cuán frequentemente predicen lo mismo. Entonces use la función heatmap para visualizar los resultados. Sugerencia: use el argumento method = "binary" en la función dist.
9. Avanzado: Tenga en cuenta que cada método también puede producir una probabilidad condicional estimada. En lugar del voto mayoritario, podemos tomar el promedio de estas probabilidades condicionales estimadas. Para la mayoría de los métodos, podemos usar el type = "prob" en la función train. Sin embargo, algunos de los métodos requieren que use el argumento trControl=trainControl(classProbs=TRUE) al llamar train. Además, estos métodos no funcionan si las clases tienen números como nombres. Sugerencia: cambie los niveles de esta manera:
dat$train$y <- recode_factor(dat$train$y, "2"="two", "7"="seven")
dat$test$y <- recode_factor(dat$test$y, "2"="two", "7"="seven")10. En este capítulo, ilustramos un par de algoritmos de machine learning en un subconjunto del set de datos MNIST. Intente ajustar un modelo a todo el set de datos.