Capítulo 2 Lo básico de R

En este libro, utilizaremos el ambiente de software R para todo nuestro análisis. Aprenderán R y las técnicas de análisis de datos simultáneamente. Por lo tanto, para continuar necesitarán acceso a R. También recomendamos el uso de un Entorno de Desarrollo Integrado (IDE), como RStudio, para guardar su trabajo. Recuerden que es común que un curso o taller ofrezca acceso a un ambiente de R y a un IDE a través de su navegador de web, como lo hace RStudio cloud¹¹. Si tienen acceso a dicho recurso, no necesitan instalar R ni RStudio. Sin embargo, si eventualmente quieren convertirse en analistas expertos de datos, recomendamos instalar estas herramientas en su computadora¹². Tanto R como RStudio son gratuitos y están disponibles en línea.

2.1 Caso de estudio: los asesinatos con armas en EE. UU.

Imagínense que viven en Europa y se les ofrece un trabajo en una empresa estadounidense con muchas ubicaciones por todo EE. UU. Es un gran trabajo, pero noticias con titulares como Tasa de homicidios con armas de fuego de EE. UU. más alta que en otros países desarrollados¹³. ¿Se preocupan? Gráficos como el siguiente pueden preocuparle aún más:

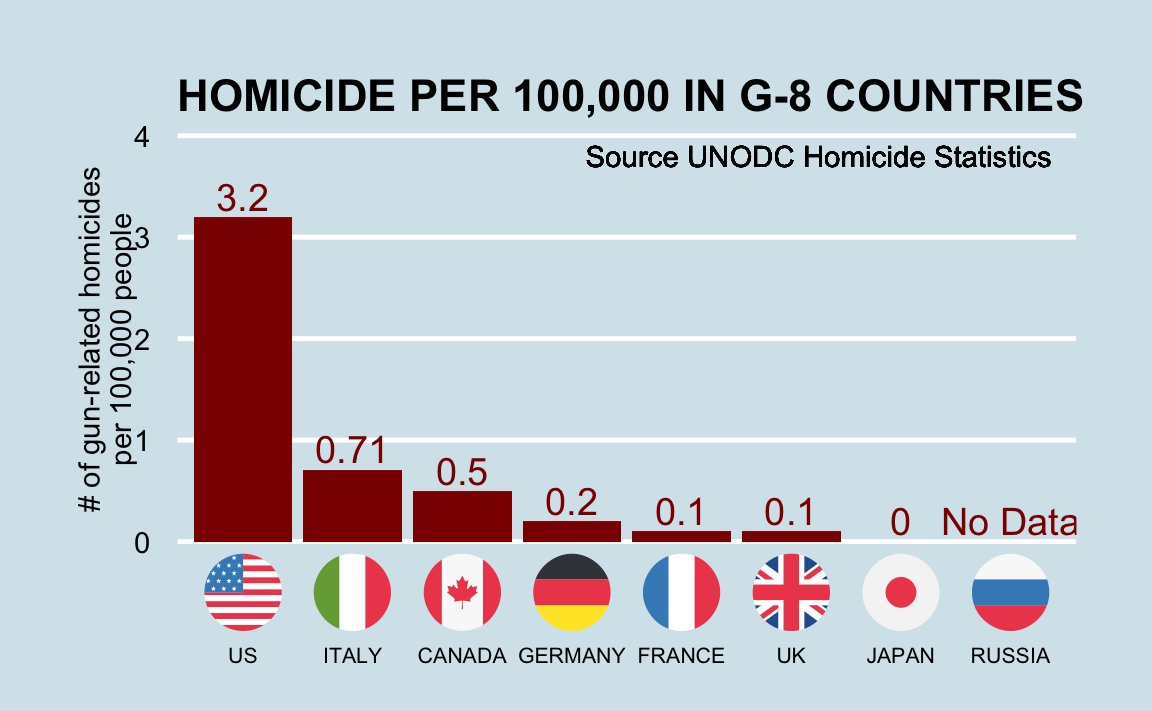
O peor aún, esta versión de everytown.org:

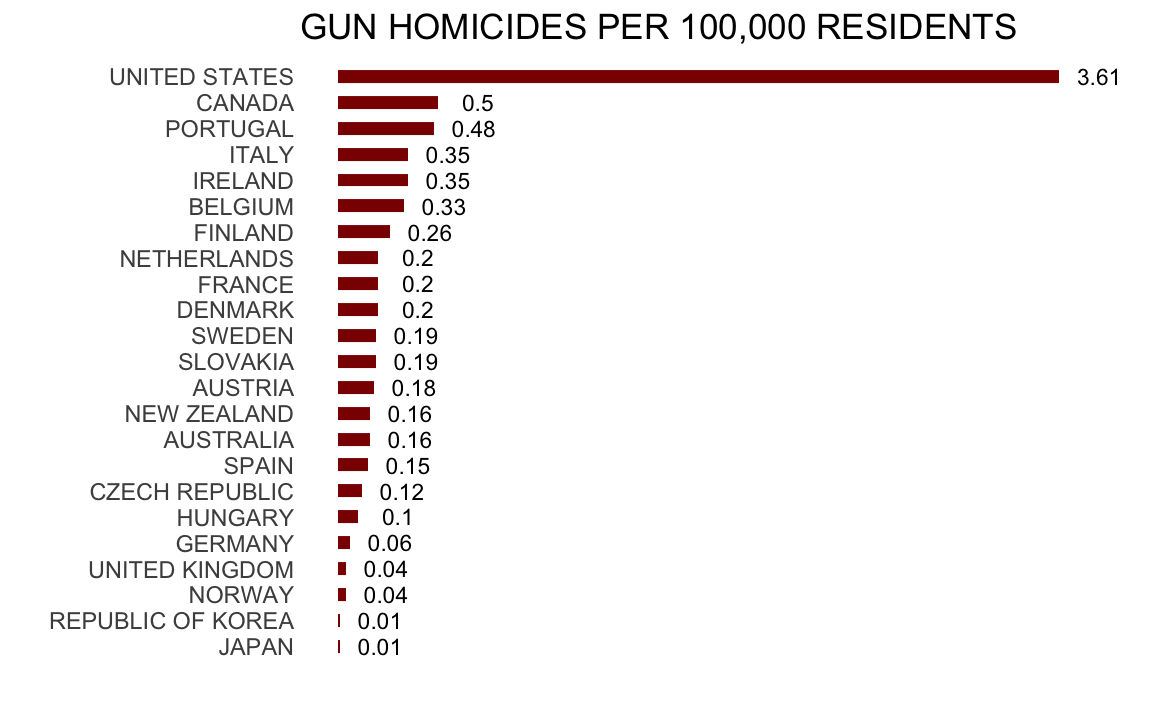
Pero entonces se recuerdan que Estados Unidos es un país grande y diverso, con 50 estados muy diferentes, además del Distrito de Columbia (DC).

#> Warning: It is deprecated to specify `guide = FALSE` to remove a guide.
#> Please use `guide = "none"` instead.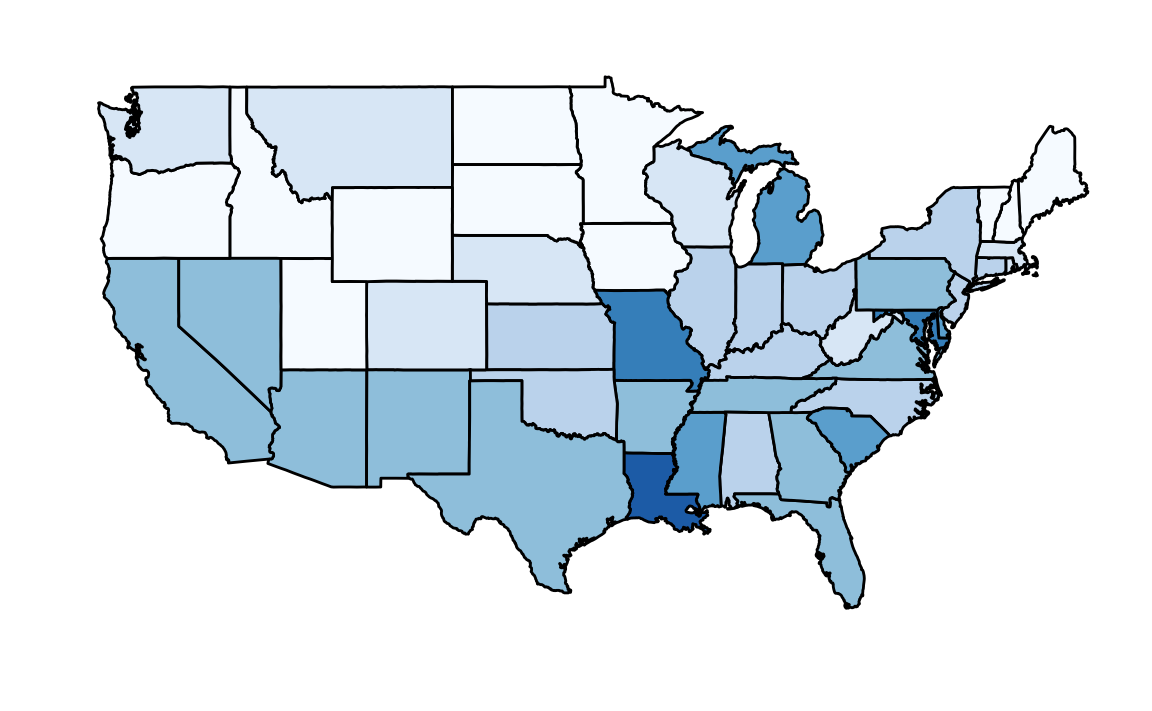

California, por ejemplo, tiene una población más grande que Canadá, y 20 estados de EE. UU. tienen poblaciones más grandes que la de Noruega. En algunos aspectos, la variabilidad entre los estados de EE. UU. es parecida a la variabilidad entre los países de Europa. Además, aunque no se incluyen en los cuadros anteriores, las tasas de asesinatos en Lituania, Ucrania y Rusia son superiores a cuatro por cada 100,000. Entonces, es posible que las noticias que les preocupan sean demasiado superficiales. Tienen opciones de dónde pueden vivir y desean determinar la seguridad de cada estado en particular. Obtendremos algunas ideas al examinar los datos relacionados con asesinatos con armas de fuego de EE. UU. en 2010 usando R.

Antes de comenzar con nuestro ejemplo, necesitamos discutir la logística, así como algunos de los componentes básicos necesarios para obtener destrezas más avanzadas de R. Recuerden que la utilidad de algunos de estos componentes básicos no siempre es inmediatamente obvia, pero más tarde en el libro apreciarán haber dominado estas destrezas.

2.2 Lo básico

Antes de empezar con el set de datos motivante, necesitamos repasar los conceptos básicos de R.

2.2.1 Objetos

Supongan que unos estudiantes de secundaria nos piden ayuda para resolver varias ecuaciones cuadráticas de la forma \(ax^2+bx+c = 0\). La fórmula cuadrática nos ofrece las soluciones:

\[ \frac{-b - \sqrt{b^2 - 4ac}}{2a}\,\, \mbox{ and } \frac{-b + \sqrt{b^2 - 4ac}}{2a} \] que por supuesto cambian dependiendo de los valores de \(a\), \(b\) y \(c\). Una ventaja de los lenguajes de programación es poder definir variables y escribir expresiones con estas, como se hace en las matemáticas, para obtener una solución numérica. Escribiremos un código general para la ecuación cuadrática a continuación, pero si nos piden resolver \(x^2 + x -1 = 0\), entonces definimos:

a <- 1
b <- 1
c <- -1

que almacena los valores para su uso posterior. Usamos <- para asignar valores a las variables.

También podemos asignar valores usando = en lugar de <-, pero recomendamos no usar = para evitar confusión.

Copien y peguen el código anterior en su consola para definir las tres variables. Tengan en cuenta que R no imprime nada cuando hacemos esta asignación. Esto significa que los objetos se definieron con éxito. Si hubieran cometido un error, recibirían un mensaje de error.

Para ver el valor almacenado en una variable, simplemente le pedimos a R que evalúe a y R nos muestra el valor almacenado:

a
#> [1] 1

Una forma más explícita de pedirle a R que nos muestre el valor almacenado en a es usar print así:

print(a)
#> [1] 1

Usamos el término objeto para describir cosas que están almacenadas en R. Las variables son un ejemplo, pero los objetos también pueden ser entidades más complicadas como las funciones, que se describen más adelante.

2.2.2 El espacio de trabajo

A medida que definimos objetos en la consola, estamos cambiando el espacio de trabajo (workspace en inglés). Pueden ver todas las variables guardadas en su espacio de trabajo al escribir:

ls()
#> [1] "a"        "b"        "c"        "dat"      "img_path" "murders"

En RStudio, la pestaña Environment muestra los valores:

Deberíamos ver a, b y c. Si intentan obtener el valor de una variable que no está en su espacio de trabajo, recibirán un mensaje de error. Por ejemplo, si escriben x, verán lo siguiente: Error: object 'x' not found.

Ahora, dado que estos valores se guardan en variables, para resolver nuestra ecuación, utilizamos la fórmula cuadrática:

(-b + sqrt(b^2 - 4*a*c) )/ ( 2*a )
#> [1] 0.618
(-b - sqrt(b^2 - 4*a*c) )/ ( 2*a )
#> [1] -1.62

2.2.3 Funciones

Una vez que definan las variables, el proceso de análisis de datos generalmente se puede describir como una serie de funciones aplicadas a los datos. R incluye varias funciones predefinidas y la mayoría de las líneas de análisis que construimos hacen uso extensivo de ellas.

Ya usamos las funciones install.packages, library y ls. También usamos la función sqrt para solucionar la ecuación cuadrática anterior. Hay muchas más funciones predefinidas y se pueden añadir hasta más a través de paquetes. Estas no aparecen en sus espacios de trabajo porque no las definieron, pero están disponibles para su uso inmediato.

En general, necesitamos usar paréntesis para evaluar una función. Si escriben ls, la función no se evalúa y en cambio R les muestra el código que la define. Si escriben ls(), la función se evalúa y, como ya se mostró, vemos objetos en el espacio de trabajo.

A diferencia de ls, la mayoría de las funciones requieren uno o más argumentos. A continuación se muestra un ejemplo de cómo asignamos un objeto al argumento de la función log. Recuerden que anteriormente definimos a como 1:

log(8)
#> [1] 2.08
log(a)
#> [1] 0

Pueden averiguar lo que la función espera y lo que hace revisando unos manuales muy útiles incluidos en R. Pueden obtener ayuda utilizando la función help así:

help("log")

Para la mayoría de las funciones, también podemos usar esta abreviatura:

?log

La página de ayuda les mostrará qué argumentos espera la función. Por ejemplo, log necesita x y base para correr. Sin embargo, algunos argumentos son obligatorios y otros son opcionales. Pueden determinar cuáles son opcionales notando en el documento de ayuda cuáles valores predeterminados se asignan con =. Definir estos es opcional. Por ejemplo, la base de la función log por defecto es base = exp(1) que hace log el logaritmo natural por defecto.

Para echar un vistazo rápido a los argumentos sin abrir el sistema de ayuda, pueden escribir:

args(log)
#> function (x, base = exp(1)) 
#> NULL

Pueden cambiar los valores predeterminados simplemente asignando otro objeto:

log(8, base = 2)
#> [1] 3

Recuerden que no hemos estado especificando el argumento x como tal:

log(x = 8, base = 2)
#> [1] 3

El código anterior funciona, pero también podemos ahorrarnos un poco de escritura: si no usan un nombre de argumento, R supone que están ingresando argumentos en el orden en que se muestran en la página de ayuda o por args. Entonces, al no usar los nombres, R supone que los argumentos son x seguido por base:

log(8,2)
#> [1] 3

Si usan los nombres de los argumentos, podemos incluirlos en el orden en que queramos:

log(base = 2, x = 8)
#> [1] 3

Para especificar argumentos, debemos usar = y no <-.

Hay algunas excepciones a la regla de que las funciones necesitan los paréntesis para ser evaluadas. Entre estas, las más utilizados son los operadores aritméticos y relacionales. Por ejemplo:

2^3
#> [1] 8

Pueden ver los operadores aritméticos al escribir:

help("+")

o

?"+"

y los operadores relacionales al escribir:

help(">")

o

?">"

2.2.4 Otros objetos predefinidos

Hay varios sets de datos que se incluyen para que los usuarios practiquen y prueben las funciones. Pueden ver todos los sets de datos disponibles escribiendo:

data()

Esto les muestra el nombre del objeto para estos sets de datos. Estos sets de datos son objetos que se pueden usar simplemente escribiendo el nombre. Por ejemplo, si escriben:

co2

R les mostrará los datos de concentración de CO2 atmosférico de Mauna Loa.

Otros objetos predefinidos son cantidades matemáticas, como la constante \(\pi\) e \(\infty\):

pi
#> [1] 3.14
Inf+1
#> [1] Inf

2.2.5 Nombres de variables

Hemos usado las letras a, b y c como nombres de variables, pero estos pueden ser casi cualquier cosa. Algunas reglas básicas en R son que los nombres de variables tienen que comenzar con una letra, no pueden contener espacios y no deben ser variables predefinidas en R. Por ejemplo, no nombren una de sus variables install.packages escribiendo algo como: install.packages <- 2.

Una buena convención a seguir es usar palabras significativas que describan lo que están almacenado, usar solo minúsculas y usar guiones bajos como sustituto de espacios. Para las ecuaciones cuadráticas, podríamos usar algo como:

solution_1 <- (-b + sqrt(b^2 - 4*a*c))/ (2*a)
solution_2 <- (-b - sqrt(b^2 - 4*a*c))/ (2*a)

Para obtener más consejos, recomendamos estudiar la guía de estilo de Hadley Wickham¹⁴.

2.2.6 Cómo guardar su espacio de trabajo

Los valores permanecen en el espacio de trabajo hasta que finalicen sus sesiones o las borren con la función rm. Pero los espacios de trabajo también se pueden guardar para su uso posterior. De hecho, al salir de R, el programa les pregunta si desean guardar su espacio de trabajo. Si lo guardan, la próxima vez que inicien R, el programa restaurará el espacio de trabajo.

Sin embargo, no recomendamos guardar el espacio de trabajo así porque, a medida que comiencen a trabajar en diferentes proyectos, será más difícil darle seguimiento de lo que guardan. En cambio, les recomendamos que le asignen al espacio de trabajo un nombre específico. Pueden hacer esto usando las funciones save o save.image. Para cargar, usen la función load. Al guardar un espacio de trabajo, recomendamos el sufijo rda o RData. En RStudio, también pueden hacerlo navegando a la pestaña Session y eligiendo Save Workspace as. Luego pueden cargarlo usando las opciones Load Workspace en la misma pestaña. Para aprender más, lean las páginas de ayuda (help pages en inglés) en save, save.image y load.

2.2.7 Scripts motivantes

Para resolver otra ecuación como \(3x^2 + 2x -1\), podemos copiar y pegar el código anterior, redefinir las variables y volver a calcular la solución:

a <- 3
b <- 2
c <- -1
(-b + sqrt(b^2 - 4*a*c))/ (2*a)
(-b - sqrt(b^2 - 4*a*c))/ (2*a)

Al crear y guardar un script con el código anterior, ya no tendrán que volver a escribirlo todo cada vez, sino simplemente cambiar los nombres de las variables. Intenten escribir la secuencia de comandos anteriores en un editor y observen lo fácil que es cambiar las variables y recibir una respuesta.

2.2.8 Cómo comentar su código

Si una línea de código R comienza con el símbolo #, no se evalúa. Podemos usar esto para escribir recordatorios de por qué escribimos un código particular. Por ejemplo, en el script anterior, podríamos añadir:

## Código para calcular la solución a la 
## ecuación cuadrática de la forma ax^2 + bx + c
## definir las variables
a <- 3
b <- 2
c <- -1

## ahora calcule la solución
(-b + sqrt(b^2 - 4*a*c)) / (2*a)
(-b - sqrt(b^2 - 4*a*c)) / (2*a)

2.3 Ejercicios

1. ¿Cuál es la suma de los primeros 100 números enteros positivos? La fórmula para la suma de enteros \(1\) a \(n\) es \(n(n+1)/2\). Defina \(n=100\) y luego use R para calcular la suma de \(1\) a \(100\) usando la fórmula. ¿Cuál es la suma?

2. Ahora use la misma fórmula para calcular la suma de los enteros del 1 a 1000.

3. Mire el resultado de escribir el siguiente código en R:

n <- 1000
x <- seq(1, n)
sum(x)

Basado en el resultado, ¿qué cree que hacen las funciones seq y sum? Puede usar help.

1. sum crea una lista de números y seq los suma.
2. seq crea una lista de números y sum los suma.
3. seq crea una lista aleatoria y sum calcula la suma de 1 a 1000.
4. sum siempre devuelve el mismo número.

4. En las matemáticas y la programación decimos que evaluamos una función cuando reemplazamos el argumento con un número dado. Entonces si escribimos sqrt(4), evaluamos la función sqrt. En R se puede evaluar una función dentro de otra función. Las evaluaciones suceden de adentro hacia afuera. Use una línea de código para calcular el logaritmo, en base 10, de la raíz cuadrada de 100.

5. ¿Cuál de los siguientes siempre devolverá el valor numérico almacenado en x? Puede intentar los ejemplos y usar el sistema de ayuda si lo desea.

1. log(10^x)
2. log10(x^10)
3. log(exp(x))
4. exp(log(x, base = 2))

2.4 Tipos de datos

Las variables en R pueden ser de diferentes tipos. Por ejemplo, necesitamos distinguir números de cadenas de caracteres y tablas de listas sencillas de números. La función class nos ayuda a determinar qué tipo de objeto tenemos:

a <- 2
class(a)
#> [1] "numeric"

Para trabajar eficientemente en R, es importante aprender los diferentes tipos de variables y qué podemos hacer con ellos.

2.4.1 Data frames

Hasta ahora, las variables que hemos definido son solo un número. Esto no es muy útil para almacenar datos. La forma más común de almacenar un set de datos en R es usando un data frame. Conceptualmente, podemos pensar en un data frame como una tabla con filas que representan observaciones y con columnas que representan las diferentes variables recopiladas para cada observación. Los data frames son particularmente útiles para sets de datos porque podemos combinar diferentes tipos de datos en un solo objeto.

Una gran proporción de los retos del análisis de datos comienza con datos almacenados en un data frame. Por ejemplo, almacenamos los datos para nuestro ejemplo motivante en un data frame. Pueden tener acceso a este set de datos cargando el paquete dslabs y entonces utilizando la función data para cargar el set de datos murders :

library(dslabs)
data(murders)

Para verificar que esto es un data frame, escribimos:

class(murders)
#> [1] "data.frame"

2.4.2 Cómo examinar un objeto

La función str es útil para obtener más información sobre la estructura de un objeto:

str(murders)
#> 'data.frame':    51 obs. of  5 variables:
#> $ state : chr "Alabama" "Alaska" "Arizona" "Arkansas" ...
#> $ abb : chr "AL" "AK" "AZ" "AR" ...
#> $ region : Factor w/ 4 levels "Northeast","South",..: 2 4 4 2 4 4 1 2 2
#>    2 ...
#> $ population: num 4779736 710231 6392017 2915918 37253956 ...
#> $ total : num 135 19 232 93 1257 ...

Esto nos dice mucho más sobre el objeto. Vemos que la tabla tiene 51 filas (50 estados más DC) y cinco variables. Podemos mostrar las primeras seis líneas usando la función head:

head(murders)
#>        state abb region population total
#> 1    Alabama  AL  South    4779736   135
#> 2     Alaska  AK   West     710231    19
#> 3    Arizona  AZ   West    6392017   232
#> 4   Arkansas  AR  South    2915918    93
#> 5 California  CA   West   37253956  1257
#> 6   Colorado  CO   West    5029196    65

En este set de datos, cada estado se considera una observación y se incluyen cinco variables para cada estado.

Antes de continuar respondiendo a nuestra pregunta original sobre los diferentes estados, repasemos más sobre los componentes de este objeto.

2.4.3 El operador de acceso: $

Para nuestro análisis, necesitaremos acceso a las diferentes variables representadas por columnas incluidas en este data frame. Para hacer esto, utilizamos el operador de acceso $ de la siguiente manera:

murders$population
#>  [1]  4779736   710231  6392017  2915918 37253956  5029196  3574097
#>  [8]   897934   601723 19687653  9920000  1360301  1567582 12830632
#> [15]  6483802  3046355  2853118  4339367  4533372  1328361  5773552
#> [22]  6547629  9883640  5303925  2967297  5988927   989415  1826341
#> [29]  2700551  1316470  8791894  2059179 19378102  9535483   672591
#> [36] 11536504  3751351  3831074 12702379  1052567  4625364   814180
#> [43]  6346105 25145561  2763885   625741  8001024  6724540  1852994
#> [50]  5686986   563626

¿Pero cómo supimos usar population? Anteriormente, aplicando la función str al objeto murders, revelamos los nombres de cada una de las cinco variables almacenadas en esta tabla. Podemos tener acceso rápido a los nombres de las variables usando:

names(murders)
#> [1] "state"      "abb"        "region"     "population" "total"

Es importante saber que el orden de las entradas en murders$population conserva el orden de las filas en nuestra tabla de datos. Esto luego nos permitirá manipular una variable basada en los resultados de otra. Por ejemplo, podremos ordenar los nombres de los estados según el número de asesinatos.

Consejo: R viene con una muy buena funcionalidad de autocompletar que nos ahorra la molestia de escribir todos los nombres. Escriban murders$p y luego presionen la tecla tab en su teclado. Esta funcionalidad y muchas otras características útiles de autocompletar están disponibles en RStudio.

2.4.4 Vectores: numéricos, de caracteres y lógicos

El objeto murders$population no es un número sino varios. Llamamos vectores a este tipo de objeto. Un solo número es técnicamente un vector de longitud 1, pero en general usamos el término vectores para referirnos a objetos con varias entradas. La función length les dice cuántas entradas hay en el vector:

pop <- murders$population
length(pop)
#> [1] 51

Este vector particular es numérico ya que los tamaños de la población son números:

class(pop)
#> [1] "numeric"

En un vector numérico cada entrada debe ser un número.

Para almacenar una cadena de caracteres, los vectores también pueden ser de la clase carácter. Por ejemplo, los nombres de los estados son caracteres:

class(murders$state)
#> [1] "character"

Al igual que con los vectores numéricos, todas las entradas en un vector de caracteres deben ser un carácter.

Otro tipo importante de vectores son los vectores lógicos. Estos deben ser TRUE o FALSE.

z <- 3 == 2
z
#> [1] FALSE
class(z)
#> [1] "logical"

Aquí el == es un operador relacional que pregunta si 3 es igual a 2. En R, usar solo un = asigna una variable, pero si usan dos ==, entonces evalúa si los objetos son iguales.

Pueden ver esto al escribir:

?Comparison

En futuras secciones, observarán lo útil que pueden ser los operadores relacionales.

Discutimos las características más importantes de los vectores después de los siguientes ejercicios.

Avanzado: Matemáticamente, los valores en pop son números enteros y hay una clase de enteros en R. Sin embargo, por defecto, a los números se les asigna una clase numérica incluso cuando son enteros redondos. Por ejemplo, class(1) devuelve numérico. Pueden convertirlo en un entero de clase con la función as.integer() o agregando un L así: 1L. Tengan en cuenta la clase escribiendo: class(1L).

2.4.5 Factores

En el set de datos murders, se podría esperar que la región también sea un vector de caracteres. Sin embargo, no lo es:

class(murders$region)
#> [1] "factor"

Es un factor. Los factores son útiles para almacenar datos categóricos. Podemos ver que solo hay cuatro regiones al utilizar la función levels:

levels(murders$region)
#> [1] "Northeast"     "South"         "North Central" "West"

En el fondo, R almacena estos levels como números enteros y mantiene un mapa para llevar un registro de las etiquetas. Esto es más eficiente en terminos de memoria que almacenar todos los caracteres.

Tengan en cuenta que los niveles tienen un orden diferente al orden de aparición en el factor. En R, por defecto, los niveles se ordenan alfabéticamente. Sin embargo, a menudo queremos que los niveles sigan un orden diferente. Pueden especificar un orden a través del argumento levels cuando crean el factor con la función factor. Por ejemplo, en el set de datos de asesinatos, las regiones se ordenan de este a oeste. La función reorder nos permite cambiar el orden de los niveles de un factor según un resumen calculado en un vector numérico. Demostraremos esto con un ejemplo sencillo y veremos otros más avanzados en la parte Visualización de Datos del libro.

Supongan que queremos que los levels de la región se ordenen según el número total de asesinatos en vez de por orden alfabético. Si hay valores asociados con cada level, podemos usar reorder y especificar un resumen de datos para determinar el orden. El siguiente código toma la suma del total de asesinatos en cada región y reordena el factor según estas sumas.

region <- murders$region
value <- murders$total
region <- reorder(region, value, FUN = sum)
levels(region)
#> [1] "Northeast"     "North Central" "West"          "South"

El nuevo orden concuerda con el hecho de que hay menos asesinatos en el Noreste y más en el Sur.

Advertencia: Los factores pueden causar confusión ya que a veces se comportan como caracteres y otras veces no. Como resultado, estos son una fuente común de errores.

2.4.6 Listas

Los data frames son un caso especial de listas. Las listas son útiles porque pueden almacenar cualquier combinación de diferentes tipos de datos. Pueden crear una lista utilizando la función lista así:

record <- list(name = "John Doe",
               student_id = 1234,
               grades = c(95, 82, 91, 97, 93),
               final_grade = "A")

La función c se describe en la sección 2.6.

Esta lista incluye un carácter, un número, un vector con cinco números y otro carácter.

record
#> $name
#> [1] "John Doe"
#> 
#> $student_id
#> [1] 1234
#> 
#> $grades
#> [1] 95 82 91 97 93
#> 
#> $final_grade
#> [1] "A"
class(record)
#> [1] "list"

Al igual que con los data frames, pueden extraer los componentes de una lista con el operador de acceso: $.

record$student_id
#> [1] 1234

También podemos usar corchetes dobles ([[) así:

record[["student_id"]]
#> [1] 1234

Deben acostumbrarse al hecho de que, en R, frecuentemente hay varias formas de hacer lo mismo, como tener acceso a las entradas.

También pueden encontrar listas sin nombres de variables:

record2 <- list("John Doe", 1234)
record2
#> [[1]]
#> [1] "John Doe"
#> 
#> [[2]]
#> [1] 1234

Si una lista no tiene nombres, no pueden extraer los elementos con $, pero todavía pueden usar el método de corchetes. En vez de proveer el nombre de la variable, pueden proveer el índice de la lista de la siguiente manera:

record2[[1]]
#> [1] "John Doe"

No usaremos listas hasta más tarde, pero es posible que encuentren una en sus propias exploraciones de R. Por eso, les mostramos algunos conceptos básicos aquí.

2.4.7 Matrices

Las matrices son otro tipo de objeto común en R. Las matrices son similares a los data frames en que son bidimensionales: tienen filas y columnas. Sin embargo, al igual que los vectores numéricos, de caracteres y lógicos, las entradas en las matrices deben ser del mismo tipo. Por esta razón, los data frames son mucho más útiles para almacenar datos, ya que podemos tener caracteres, factores y números en ellos.

No obstante, las matrices tienen una gran ventaja sobre los data frames: podemos realizar operaciones de álgebra de matrices, una técnica matemática poderosa. No describimos estas operaciones en este libro, pero gran parte de lo que sucede en segundo plano cuando se realiza un análisis de datos involucra matrices. Cubrimos las matrices con más detalle en el Capítulo 33.1 pero también las discutimos brevemente aquí, ya que algunas de las funciones que aprenderemos devuelven matrices.

Podemos definir una matriz usando la función matrix. Necesitamos especificar el número de filas y columnas:

mat <- matrix(1:12, 4, 3)
mat
#>      [,1] [,2] [,3]
#> [1,]    1    5    9
#> [2,]    2    6   10
#> [3,]    3    7   11
#> [4,]    4    8   12

Pueden acceder a entradas específicas en una matriz usando corchetes ([). Si desean la segunda fila, tercera columna, escriban:

mat[2, 3]
#> [1] 10

Si desean toda la segunda fila, dejen vacío el lugar de la columna:

mat[2, ]
#> [1]  2  6 10

Noten que esto devuelve un vector, no una matriz.

Del mismo modo, si desean la tercera columna completa, dejen el lugar de la fila vacío:

mat[, 3]
#> [1]  9 10 11 12

Esto también es un vector, no una matriz.

Pueden acceder a más de una columna o más de una fila si lo desean. Esto les dará una nueva matriz:

mat[, 2:3]
#>      [,1] [,2]
#> [1,]    5    9
#> [2,]    6   10
#> [3,]    7   11
#> [4,]    8   12

Pueden crear subconjuntos basados tanto en las filas como en las columnas:

mat[1:2, 2:3]
#>      [,1] [,2]
#> [1,]    5    9
#> [2,]    6   10

Podemos convertir las matrices en data frames usando la función as.data.frame:

as.data.frame(mat)
#>   V1 V2 V3
#> 1  1  5  9
#> 2  2  6 10
#> 3  3  7 11
#> 4  4  8 12

También podemos usar corchetes individuales ([) para acceder a las filas y las columnas de un data frame:

data("murders")
murders[25, 1]
#> [1] "Mississippi"
murders[2:3, ]
#>     state abb region population total
#> 2  Alaska  AK   West     710231    19
#> 3 Arizona  AZ   West    6392017   232

2.5 Ejercicios

1. Cargue el set de datos de asesinatos de EE.UU.

library(dslabs)
data(murders)

Use la función str para examinar la estructura del objeto murders. ¿Cuál de las siguientes opciones describe mejor las variables representadas en este data frame?

1. Los 51 estados.
2. Las tasas de asesinatos para los 50 estados y DC.
3. El nombre del estado, la abreviatura del nombre del estado, la región del estado y la población y el número total de asesinatos para 2010 del estado.
4. str no muestra información relevante.

2. ¿Cuáles son los nombres de las columnas utilizados por el data frame para estas cinco variables?

3. Use el operador de acceso $ para extraer las abreviaturas de los estados y asignarlas al objeto a. ¿Cuál es la clase de este objeto?

4. Ahora use los corchetes para extraer las abreviaturas de los estados y asignarlas al objeto b. Utilice la función identical para determinar si a y b son iguales.

5. Vimos que la columna region almacena un factor. Puede corroborar esto escribiendo:

class(murders$region)

Con una línea de código, use las funciones levels y length para determinar el número de regiones definidas por este set de datos.

6. La función table toma un vector y devuelve la frecuencia de cada elemento. Puede ver rápidamente cuántos estados hay en cada región aplicando esta función. Use esta función en una línea de código para crear una tabla de estados por región.

2.6 Vectores

En R, los objetos más básicos disponibles para almacenar datos son vectores. Como hemos visto, los sets de datos complejos generalmente se pueden dividir en componentes que son vectores. Por ejemplo, en un data frame, cada columna es un vector. Aquí aprendemos más sobre esta clase importante.

2.6.1 Cómo crear vectores

Podemos crear vectores usando la función c, que significa concatenar. Usamos c para concatenar entradas de la siguiente manera:

codes <- c(380, 124, 818)
codes
#> [1] 380 124 818

También podemos crear vectores de caracteres. Usamos las comillas para denotar que las entradas son caracteres en lugar de nombres de variables.

country <- c("italy", "canada", "egypt")

En R, también pueden usar comillas sencillas:

country <- c('italy', 'canada', 'egypt')

Pero tengan cuidado de no confundir la comilla sencilla ’ con el back quote `.

A estas alturas ya deberían saber que si escriben:

country <- c(italy, canada, egypt)

recibirán un error porque las variables italy, canada y egypt no están definidas. Si no usamos las comillas, R busca variables con esos nombres y devuelve un error.

2.6.2 Nombres

A veces es útil nombrar las entradas de un vector. Por ejemplo, al definir un vector de códigos de paises, podemos usar los nombres para conectar los dos:

codes <- c(italy = 380, canada = 124, egypt = 818)
codes
#>  italy canada  egypt 
#>    380    124    818

El objeto codes sigue siendo un vector numérico:

class(codes)
#> [1] "numeric"

pero con nombres:

names(codes)
#> [1] "italy"  "canada" "egypt"

Si el uso de cadenas sin comillas parece confuso, sepan que también pueden usar las comillas:

codes <- c("italy" = 380, "canada" = 124, "egypt" = 818)
codes
#>  italy canada  egypt 
#>    380    124    818

No hay diferencia entre esta llamada a una función (function call en inglés) y la anterior. Esta es una de las muchas formas en que R es peculiar en comparación con otros lenguajes.

También podemos asignar nombres usando la función names:

codes <- c(380, 124, 818)
country <- c("italy","canada","egypt")
names(codes) <- country
codes
#>  italy canada  egypt 
#>    380    124    818

2.6.3 Secuencias

Otra función útil para crear vectores genera secuencias:

seq(1, 10)
#>  [1]  1  2  3  4  5  6  7  8  9 10

El primer argumento define el inicio y el segundo define el final que se incluye en el vector. El valor por defecto es subir en incrementos de 1, pero un tercer argumento nos permite determinar cuánto saltar:

seq(1, 10, 2)
#> [1] 1 3 5 7 9

Si queremos enteros consecutivos, podemos usar la siguiente abreviación:

1:10
#>  [1]  1  2  3  4  5  6  7  8  9 10

Cuando usamos estas funciones, R produce números enteros, no numéricos, porque generalmente se usan para indexar algo:

class(1:10)
#> [1] "integer"

Sin embargo, si creamos una secuencia que incluye no enteros, la clase cambia:

class(seq(1, 10, 0.5))
#> [1] "numeric"

2.6.4 Cómo crear un subconjunto

Usamos los corchetes para tener acceso a elementos específicos de un vector. Para el vector codes que definimos anteriormente, podemos tener acceso al segundo elemento usando:

codes[2]
#> canada 
#>    124

Pueden obtener más de una entrada utilizando un vector de entradas múltiples como índice:

codes[c(1,3)]
#> italy egypt 
#>   380   818

Las secuencias definidas anteriormente son particularmente útiles si necesitamos acceso, digamos, a los dos primeros elementos:

codes[1:2]
#>  italy canada 
#>    380    124

Si los elementos tienen nombres, también podemos acceder a las entradas utilizando estos nombres. A continuación ofrecemos dos ejemplos:

codes["canada"]
#> canada 
#>    124
codes[c("egypt","italy")]
#> egypt italy 
#>   818   380

2.7 La conversión forzada

En general, la conversión forzada (coercion en inglés) es un intento de R de ser flexible con los tipos de datos. Cuando una entrada no coincide con lo esperado, algunas de las funciones predefinidas de R tratan de adivinar lo que uno intentaba antes de devolver un mensaje de error. Esto también puede causar confusión. Al no entender la conversión forzada, los programadores pueden volverse locos cuando codifican en R, ya que R se comporta de manera bastante diferente a la mayoría de los otros idiomas en cuanto a esto. Aprendamos más con unos ejemplos.

Dijimos que los vectores deben ser todos del mismo tipo. Entonces, si tratamos de combinar, por ejemplo, números y caracteres, pueden esperar un error:

x <- c(1, "canada", 3)

¡Pero no nos da un error, ni siquiera una advertencia! ¿Que pasó? Miren x y su clase:

x
#> [1] "1"      "canada" "3"
class(x)
#> [1] "character"

R forzó una conversión de los datos a caracteres. Como pusimos una cadena de caracteres en el vector, R adivinó que nuestra intención era que el 1 y el 3 fueran las cadenas de caracteres "1" y “3”. El hecho de que ni siquiera emitiera una advertencia es un ejemplo de cómo la conversión forzada puede causar muchos errores inadvertidos en R.

R también ofrece funciones para cambiar de un tipo a otro. Por ejemplo, pueden convertir números en caracteres con:

x <- 1:5
y <- as.character(x)
y
#> [1] "1" "2" "3" "4" "5"

Pueden revertir a lo anterior con as.numeric:

as.numeric(y)
#> [1] 1 2 3 4 5

Esta función es muy útil ya que los sets de datos que incluyen números como cadenas de caracteres son comunes.

2.7.1 Not available (NA)

Cuando una función intenta forzar una conversión de un tipo a otro y encuentra un caso imposible, generalmente nos da una advertencia y convierte la entrada en un valor especial llamado NA que significa no disponible (Not Available en inglés). Por ejemplo:

x <- c("1", "b", "3")
as.numeric(x)
#> Warning: NAs introducidos por coerción
#> [1]  1 NA  3

R no sabe el número que querían cuando escribieron b y no lo intenta adivinar.

Como científicos de datos, se encontrarán con el NA frecuentemente ya que se usa generalmente para datos faltantes (missing data en inglés), un problema común en los sets de datos del mundo real.

2.8 Ejercicios

1. Use la función c para crear un vector con las temperaturas altas promedio en enero para Beijing, Lagos, París, Río de Janeiro, San Juan y Toronto, que son 35, 88, 42, 84, 81 y 30 grados Fahrenheit. Llame al objeto temp.

2. Ahora cree un vector con los nombres de las ciudades y llame al objeto city.

3. Utilice la función names y los objetos definidos en los ejercicios anteriores para asociar los datos de temperatura con su ciudad correspondiente.

4. Utilice los operadores [ y : para acceder a la temperatura de las tres primeras ciudades de la lista.

5. Utilice el operador [ para acceder a la temperatura de París y San Juan.

6. Utilice el operador : para crear una secuencia de números \(12,13,14,\dots,73\).

7. Cree un vector que contenga todos los números impares positivos menores que 100.

8. Cree un vector de números que comience en 6, no pase 55 y agregue números en incrementos de 4/7: 6, 6 + 4/7, 6 + 8/7, y así sucesivamente. ¿Cuántos números tiene la lista? Sugerencia: use seq y length.

9. ¿Cuál es la clase del siguiente objeto a <- seq(1, 10, 0.5)?

10. ¿Cuál es la clase del siguiente objeto a <- seq(1, 10)?

11. La clase de class(a<-1) es numérica, no entero. R por defecto es numérico y para forzar un número entero, debe añadir la letra L. Confirme que la clase de 1L es entero.

12. Defina el siguiente vector:

x <- c("1", "3", "5")

y oblíguelo a obtener enteros.

2.9 Sorting

Ahora que hemos dominado algunos conocimientos básicos de R, intentemos obtener algunos conocimientos sobre la seguridad de los distintos estados en el contexto de los asesinatos con armas de fuego.

2.9.1 sort

Digamos que queremos clasificar los estados desde el menor hasta el mayor según los asesinatos con armas de fuego. La función sort ordena un vector en orden creciente. Por lo tanto, podemos ver la mayor cantidad de asesinatos con armas escribiendo:

library(dslabs)
data(murders)
sort(murders$total)
#>  [1]    2    4    5    5    7    8   11   12   12   16   19   21   22
#> [14]   27   32   36   38   53   63   65   67   84   93   93   97   97
#> [27]   99  111  116  118  120  135  142  207  219  232  246  250  286
#> [40]  293  310  321  351  364  376  413  457  517  669  805 1257

Sin embargo, esto no nos da información sobre qué estados tienen qué total de asesinatos. Por ejemplo, no sabemos qué estado tuvo 1257.

2.9.2 order

La función order es mas apropiada para lo que queremos hacer. order toma un vector como entrada y devuelve el vector de índices que clasifica el vector de entrada. Esto puede ser un poco confuso, así que estudiemos un ejemplo sencillo. Podemos crear un vector y ordenarlo (sort en inglés):

x <- c(31, 4, 15, 92, 65)
sort(x)
#> [1]  4 15 31 65 92

En lugar de ordenar el vector de entrada, la función order devuelve el índice que ordena el vector de entrada:

index <- order(x)
x[index]
#> [1]  4 15 31 65 92

Este es el mismo resultado que le devuelve sort(x). Si miramos este índice, vemos por qué funciona:

x
#> [1] 31  4 15 92 65
order(x)
#> [1] 2 3 1 5 4

La segunda entrada de x es la más pequeña, entonces order(x) comienza con 2. La siguiente más pequeña es la tercera entrada, por lo que la segunda entrada es 3 y así sigue.

¿Cómo nos ayuda esto a ordenar los estados por asesinatos? Primero, recuerden que las entradas de vectores a las que acceden con $ siguen el mismo orden que las filas de la tabla. Por ejemplo, estos dos vectores que contienen el nombre de los estados y sus abreviaturas, respectivamente, siguen el mismo orden:

murders$state[1:6]
#> [1] "Alabama"    "Alaska"     "Arizona"    "Arkansas"   "California"
#> [6] "Colorado"
murders$abb[1:6]
#> [1] "AL" "AK" "AZ" "AR" "CA" "CO"

Esto significa que podemos ordenar los nombres de estado según el total de asesinatos. Primero obtenemos el índice que ordena los vectores por el total de asesinatos y luego ponemos el vector de nombres de estado en un índice:

ind <- order(murders$total)
murders$abb[ind]
#>  [1] "VT" "ND" "NH" "WY" "HI" "SD" "ME" "ID" "MT" "RI" "AK" "IA" "UT"
#> [14] "WV" "NE" "OR" "DE" "MN" "KS" "CO" "NM" "NV" "AR" "WA" "CT" "WI"
#> [27] "DC" "OK" "KY" "MA" "MS" "AL" "IN" "SC" "TN" "AZ" "NJ" "VA" "NC"
#> [40] "MD" "OH" "MO" "LA" "IL" "GA" "MI" "PA" "NY" "FL" "TX" "CA"

De acuerdo con lo anterior, California tuvo la mayor cantidad de asesinatos.

2.9.3 max y which.max

Si solo estamos interesados en la entrada con el mayor valor, podemos usar max:

max(murders$total)
#> [1] 1257

y which.max para el índice del valor mayor:

i_max <- which.max(murders$total)
murders$state[i_max]
#> [1] "California"

Para el mínimo, podemos usar min y which.min del mismo modo.

¿Esto significa que California es el estado más peligroso? En una próxima sección, planteamos que deberíamos considerar las tasas en lugar de los totales. Antes de hacer eso, presentamos una última función relacionada con el orden: rank.

2.9.4 rank

Aunque no se usa con tanta frecuencia como order y sort, la función rank también está relacionada con el orden y puede ser útil. Para cualquier vector dado, rank devuelve un vector con el rango de la primera entrada, segunda entrada, etc., del vector de entrada. Aquí tenemos un ejemplo sencillo:

x <- c(31, 4, 15, 92, 65)
rank(x)
#> [1] 3 1 2 5 4

Para resumir, veamos los resultados de las tres funciones que hemos discutido:

original	sort	order	rank
31	4	2	3
4	15	3	1
15	31	1	2
92	65	5	5
65	92	4	4

2.9.5 Cuidado con el reciclaje

Otra fuente común de errores inadvertidos en R es el uso de reciclaje (recycling en inglés). Hemos visto como los vectores se agregan por elementos. Entonces, si los vectores no coinciden en longitud, es natural suponer que vamos a ver un error. Pero ese no es el caso. Vean lo que pasa:

x <- c(1, 2, 3)
y <- c(10, 20, 30, 40, 50, 60, 70)
x+y
#> Warning in x + y: longitud de objeto mayor no es múltiplo de la longitud
#> de uno menor
#> [1] 11 22 33 41 52 63 71

Recibimos una advertencia, pero no hay error. Para el output, R ha reciclado los números en x. Observen el último dígito de números en el output.

2.10 Ejercicios

Para estos ejercicios usaremos el set de datos de asesinatos de EE. UU. Asegúrense de cargarlo antes de comenzar.

library(dslabs)
data("murders")

1. Utilice el operador $ para acceder a los datos del tamaño de la población y almacenarlos como el objeto pop. Luego, use la función sort para redefinir pop para que esté en orden alfabético. Finalmente, use el operador [ para indicar el tamaño de población más pequeño.

2. Ahora, en lugar del tamaño de población más pequeño, encuentre el índice de la entrada con el tamaño de población más pequeño. Sugerencia: use order en lugar de sort.

3. Podemos realizar la misma operación que en el ejercicio anterior usando la función which.min. Escriba una línea de código que haga esto.

4. Ahora sabemos cuán pequeño es el estado más pequeño y qué fila lo representa. ¿Qué estado es? Defina una variable states para ser los nombres de los estados del data frame murders. Indique el nombre del estado con la población más pequeña.

5. Puede crear un data frame utilizando la función data.frame. Aquí un ejemplo:

temp <- c(35, 88, 42, 84, 81, 30)
city <- c("Beijing", "Lagos", "Paris", "Rio de Janeiro",
          "San Juan", "Toronto")
city_temps <- data.frame(name = city, temperature = temp)

Utilice la función rank para determinar el rango de población de cada estado desde el menos poblado hasta el más poblado. Guarde estos rangos en un objeto llamado ranks. Luego, cree un data frame con el nombre del estado y su rango. Nombre el data frame my_df.

6. Repita el ejercicio anterior, pero esta vez ordene my_df para que los estados estén en orden de menos poblado a más poblado. Sugerencia: cree un objeto ind que almacene los índices necesarios para poner en orden los valores de la población. Luego, use el operador de corchete [ para reordenar cada columna en el data frame.

7. El vector na_example representa una serie de conteos. Puede examinar rápidamente el objeto usando:

data("na_example")
str(na_example)
#>  int [1:1000] 2 1 3 2 1 3 1 4 3 2 ...

Sin embargo, cuando calculamos el promedio con la función mean, obtenemos un NA:

mean(na_example)
#> [1] NA

La función is.na devuelve un vector lógico que nos dice qué entradas son NA. Asigne este vector lógico a un objeto llamado ind y determine cuántos NAs tiene na_example.

8. Ahora calcule nuevamente el promedio, pero solo para las entradas que no son NA. Sugerencia: recuerde el operador !.

2.11 Aritmética de vectores

California tuvo la mayor cantidad de asesinatos, pero ¿esto significa que es el estado más peligroso? ¿Qué pasa si solo tiene muchas más personas que cualquier otro estado? Podemos confirmar rápidamente que California tiene la mayor población:

library(dslabs)
data("murders")
murders$state[which.max(murders$population)]
#> [1] "California"

con más de 37 millones de habitantes. Por lo tanto, es injusto comparar los totales si estamos interesados en saber cuán seguro es el estado. Lo que realmente deberíamos calcular son los asesinatos per cápita. Los informes que describimos en la sección motivante utilizan asesinatos por cada 100,000 como la unidad. Para calcular esta cantidad, usamos las poderosas capacidades aritméticas de vectores de R.

2.11.1 Rescaling un vector

En R, las operaciones aritméticas en vectores ocurren elemento por elemento. Como ejemplo, supongan que tenemos la altura en pulgadas (inches en inglés):

inches <- c(69, 62, 66, 70, 70, 73, 67, 73, 67, 70)

y queremos convertirla a centímetros. Observen lo que sucede cuando multiplicamos inches por 2.54:

inches * 2.54
#>  [1] 175 157 168 178 178 185 170 185 170 178

Arriba, multiplicamos cada elemento por 2.54. Del mismo modo, si para cada entrada queremos calcular cuántas pulgadas más alto, o cuántas más corto, que 69 pulgadas (la altura promedio para hombres), podemos restarlo de cada entrada de esta manera:

inches - 69
#>  [1]  0 -7 -3  1  1  4 -2  4 -2  1

2.11.2 Dos vectores

Si tenemos dos vectores de la misma longitud y los sumamos en R, se agregarán entrada por entrada de la siguiente manera:

\[ \begin{pmatrix} a\\ b\\ c\\ d \end{pmatrix} + \begin{pmatrix} e\\ f\\ g\\ h \end{pmatrix} = \begin{pmatrix} a +e\\ b + f\\ c + g\\ d + h \end{pmatrix} \]

Lo mismo aplica para otras operaciones matemáticas, como -, * y /.

Esto implica que para calcular las tasas de asesinatos (murder rates en inglés) simplemente podemos escribir:

murder_rate <- murders$total/ murders$population * 100000

Al hacer esto, notamos que California ya no está cerca de la parte superior de la lista. De hecho, podemos usar lo que hemos aprendido para poner a los estados en orden por tasa de asesinatos:

murders$abb[order(murder_rate)]
#>  [1] "VT" "NH" "HI" "ND" "IA" "ID" "UT" "ME" "WY" "OR" "SD" "MN" "MT"
#> [14] "CO" "WA" "WV" "RI" "WI" "NE" "MA" "IN" "KS" "NY" "KY" "AK" "OH"
#> [27] "CT" "NJ" "AL" "IL" "OK" "NC" "NV" "VA" "AR" "TX" "NM" "CA" "FL"
#> [40] "TN" "PA" "AZ" "GA" "MS" "MI" "DE" "SC" "MD" "MO" "LA" "DC"

2.12 Ejercicios

1. Anteriormente, creamos este data frame:

temp <- c(35, 88, 42, 84, 81, 30)
city <- c("Beijing", "Lagos", "Paris", "Rio de Janeiro",
          "San Juan", "Toronto")
city_temps <- data.frame(name = city, temperature = temp)

Vuelva a crear el data frame utilizando el código anterior, pero agregue una línea que convierta la temperatura de Fahrenheit a Celsius. La conversión es \(C = \frac{5}{9} \times (F - 32)\).

2. ¿Cuál es la siguiente suma \(1+1/2^2 + 1/3^2 + \dots 1/100^2\)? Sugerencia: gracias a Euler, sabemos que debería estar cerca de \(\pi^2/6\).

3. Calcule la tasa de asesinatos por cada 100,000 para cada estado y almacénela en el objeto murder_rate. Luego, calcule la tasa promedio de asesinatos para EE. UU. con la función mean. ¿Cuál es el promedio?

2.13 Indexación

R provee una forma poderosa y conveniente de indexar vectores. Podemos, por ejemplo, crear un subconjunto de un vector según las propiedades de otro vector. En esta sección, continuamos trabajando con nuestro ejemplo de asesinatos en EE. UU., que podemos cargar así:

library(dslabs)
data("murders")

2.13.1 Cómo crear subconjuntos con lógicos

Ahora hemos calculado la tasa de asesinatos usando:

murder_rate <- murders$total/ murders$population * 100000

Imaginen que se mudan de Italia donde, según un informe de noticias, la tasa de asesinatos es solo 0.71 por 100,000. Preferirían mudarse a un estado con una tasa de asesinatos similar. Otra característica poderosa de R es que podemos usar lógicas para indexar vectores. Si comparamos un vector con un solo número, R realiza la prueba para cada entrada. Aquí tenemos un ejemplo relacionado con la pregunta anterior:

ind <- murder_rate < 0.71

Si en cambio queremos saber si un valor es menor o igual, podemos usar:

ind <- murder_rate <= 0.71

Recuerden que devuelve un vector lógico con TRUE para cada entrada menor o igual a 0.71. Para ver qué estados son estos, podemos aprovechar el hecho de que los vectores se pueden indexar con lógicos.

murders$state[ind]
#> [1] "Hawaii"        "Iowa"          "New Hampshire" "North Dakota" 
#> [5] "Vermont"

Para contar cuántos son TRUE, la función sum devuelve la suma de las entradas de un vector y fuerza una conversión de los vectores lógicos a numéricos con TRUE codificado como 1 y FALSE como 0. Así podemos contar los estados usando:

sum(ind)
#> [1] 5

2.13.2 Operadores lógicos

Supongan que nos gustan las montañas y queremos mudarnos a un estado seguro en la región occidental del país. Queremos que la tasa de asesinatos sea como máximo 1. En este caso, queremos que dos cosas diferentes sean ciertas. Aquí podemos usar el operador lógico and, que en R se representa con &. Esta operación da como resultado TRUE solo cuando ambos lógicos son TRUE, es decir ciertos. Para ver esto, consideren este ejemplo:

TRUE & TRUE
#> [1] TRUE
TRUE & FALSE
#> [1] FALSE
FALSE & FALSE
#> [1] FALSE

Para nuestro ejemplo, podemos formar dos lógicos:

west <- murders$region == "West"
safe <- murder_rate <= 1

y podemos usar & para obtener un vector lógico que nos dice qué estados satisfacen ambas condiciones:

ind <- safe & west
murders$state[ind]
#> [1] "Hawaii"  "Idaho"   "Oregon"  "Utah"    "Wyoming"

2.13.3 which

Supongan que queremos ver la tasa de asesinatos de California. Para este tipo de operación, es conveniente convertir vectores lógicos en índices en lugar de mantener vectores lógicos largos. La función which nos dice qué entradas de un vector lógico son TRUE. Entonces podemos escribir:

ind <- which(murders$state == "California")
murder_rate[ind]
#> [1] 3.37

2.13.4 match

Si en lugar de un solo estado queremos averiguar las tasas de asesinatos de varios estados, digamos Nueva York, Florida y Texas, podemos usar la función match. Esta función nos dice qué índices de un segundo vector coinciden con cada una de las entradas de un primer vector:

ind <- match(c("New York", "Florida", "Texas"), murders$state)
ind
#> [1] 33 10 44

Ahora podemos ver las tasas de asesinatos:

murder_rate[ind]
#> [1] 2.67 3.40 3.20

2.13.5 %in%

Si en lugar de un índice queremos un lógico que nos diga si cada elemento de un primer vector está en un segundo vector, podemos usar la función %in%. Imaginen que no están seguros si Boston, Dakota y Washington son estados. Pueden averiguar así:

c("Boston", "Dakota", "Washington") %in% murders$state
#> [1] FALSE FALSE  TRUE

Tengan en cuenta que estaremos usando %in% frecuentemente a lo largo del libro.

Avanzado: Hay una conexión entre match y %in% mediante which. Para ver esto, observen que las siguientes dos líneas producen el mismo índice (aunque en orden diferente):

match(c("New York", "Florida", "Texas"), murders$state)
#> [1] 33 10 44
which(murders$state%in%c("New York", "Florida", "Texas"))
#> [1] 10 33 44

2.14 Ejercicios

Empiece cargando el paquete y los datos.

library(dslabs)
data(murders)

1. Calcule la tasa de asesinatos por cada 100,000 para cada estado y almacénela en un objeto llamado murder_rate. Luego, use operadores lógicos para crear un vector lógico llamado low que nos dice qué entradas de murder_rate son inferiores a 1.

2. Ahora use los resultados del ejercicio anterior y la función which para determinar los índices de murder_rate asociados con valores inferiores a 1.

3. Use los resultados del ejercicio anterior para indicar los nombres de los estados con tasas de asesinatos inferiores a 1.

4. Ahora extienda el código de los ejercicios 2 y 3 para indicar los estados del noreste con tasas de asesinatos inferiores a 1. Sugerencia: use el vector lógico predefinido low y el operador lógico &.

5. En un ejercicio anterior, calculamos la tasa de asesinatos para cada estado y el promedio de estos números. ¿Cuántos estados están por debajo del promedio?

6. Use la función match para identificar los estados con abreviaturas AK, MI e IA. Sugerencia: comience definiendo un índice de las entradas de murders$abb que coinciden con las tres abreviaturas. Entonces use el operador [ para extraer los estados.

7. Utilice el operador %in% para crear un vector lógico que responda a la pregunta: ¿cuáles de las siguientes son abreviaturas reales: MA, ME, MI, MO, MU?

8. Extienda el código que usó en el ejercicio 7 para averiguar la única entrada que no es una abreviatura real. Sugerencia: use el operador !, que convierte FALSE a TRUE y viceversa, y entonces which para obtener un índice.

2.15 Gráficos básicos

En el capitulo 7, describimos un paquete complementario que ofrece un enfoque muy útil para producir gráficos (plots en inglés) en R. Luego tenemos una parte entera, “Visualización de datos”, en la que ofrecemos muchos ejemplos. Aquí describimos brevemente algunas de las funciones disponibles en una instalación básica de R.

2.15.1 plot

La función plot se puede utilizar para hacer diagramas de dispersión (scatterplots en inglés). Abajo tenemos un gráfico de total de asesinatos versus población.

x <- murders$population/ 10^6
y <- murders$total
plot(x, y)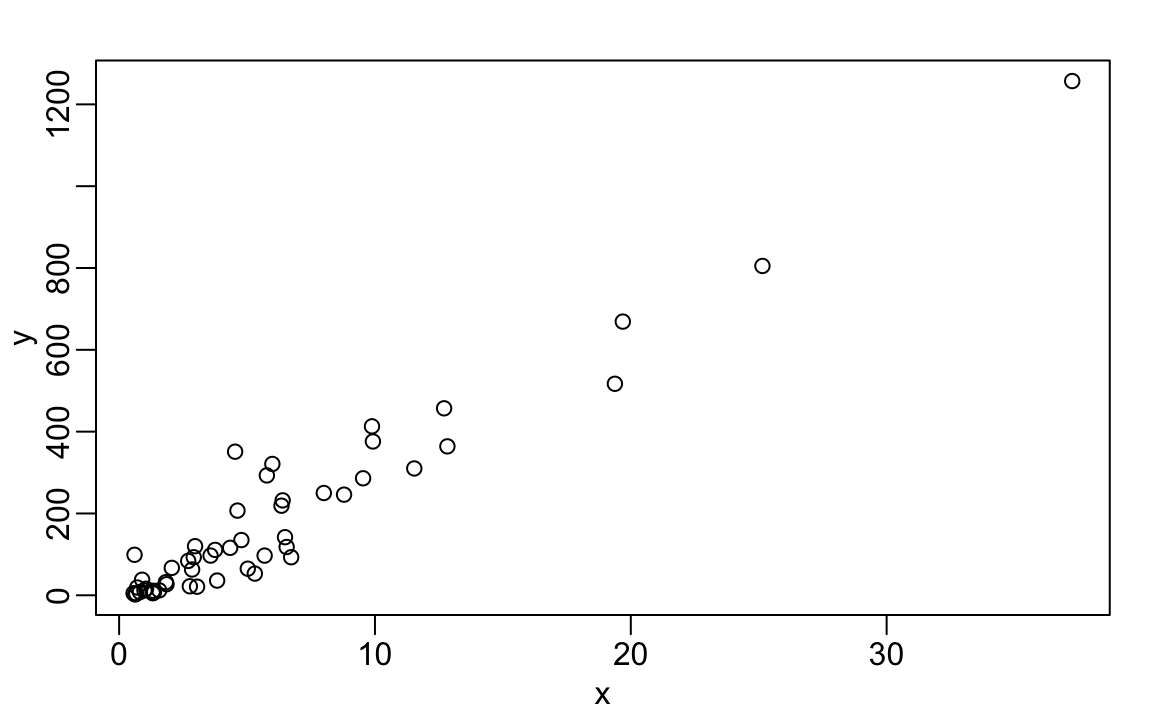

Para crear un gráfico rápido que no accede a las variables dos veces, podemos usar la función with:

with(murders, plot(population, total))

La función with nos permite usar los nombres de la columna murders en la función plot. También funciona con cualquier data frame y cualquier función.

2.15.2 hist

Describiremos los histogramas en relación con las distribuciones en la parte del libro “Visualización de datos”. Aquí simplemente notaremos que los histogramas son un resumen gráfico eficaz de una lista de números que nos ofrece una descripción general de los tipos de valores que tenemos. Podemos hacer un histograma de nuestras tasas de asesinatos al simplemente escribir:

x <- with(murders, total/ population * 100000)
hist(x)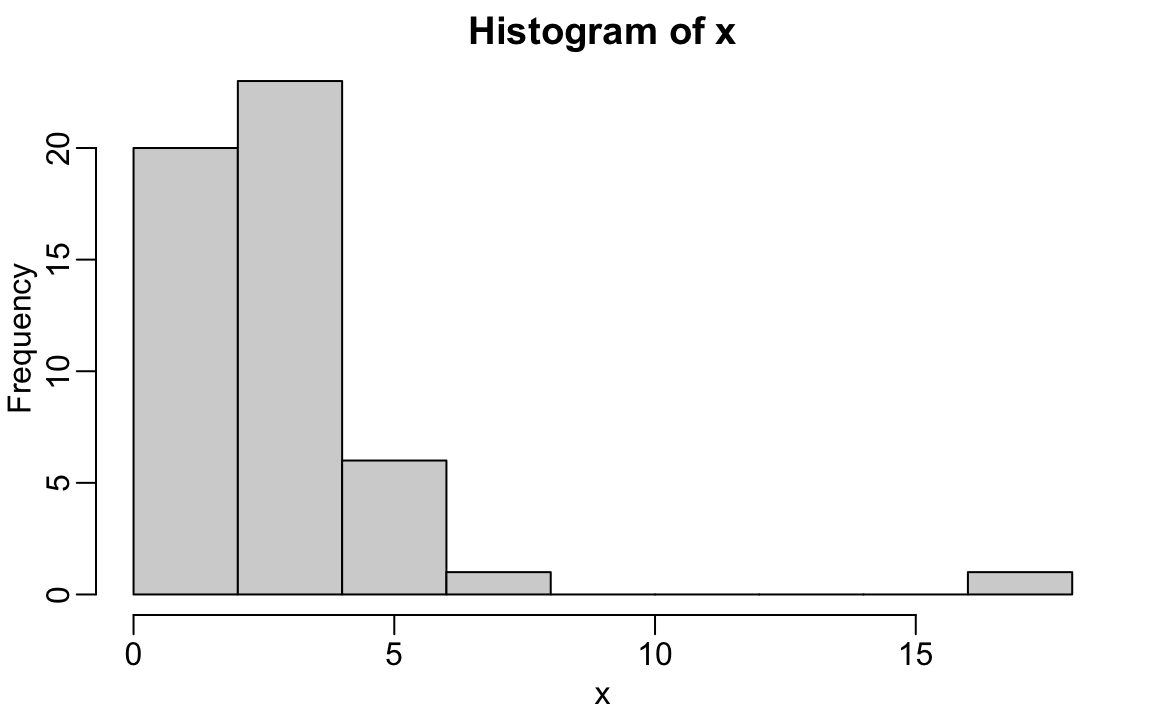

Podemos ver que hay una amplia gama de valores con la mayoría de ellos entre 2 y 3 y un caso muy extremo con una tasa de asesinatos de más de 15:

murders$state[which.max(x)]
#> [1] "District of Columbia"

2.15.3 boxplot

Los diagramas de caja (boxplots en inglés) también se describirán en la parte del libro “Visualización de datos”. Estos proveen un resumen más conciso que los histogramas, pero son más fáciles de apilar con otros diagramas de caja. Por ejemplo, aquí podemos usarlos para comparar las diferentes regiones:

murders$rate <- with(murders, total/ population * 100000)
boxplot(rate~region, data = murders)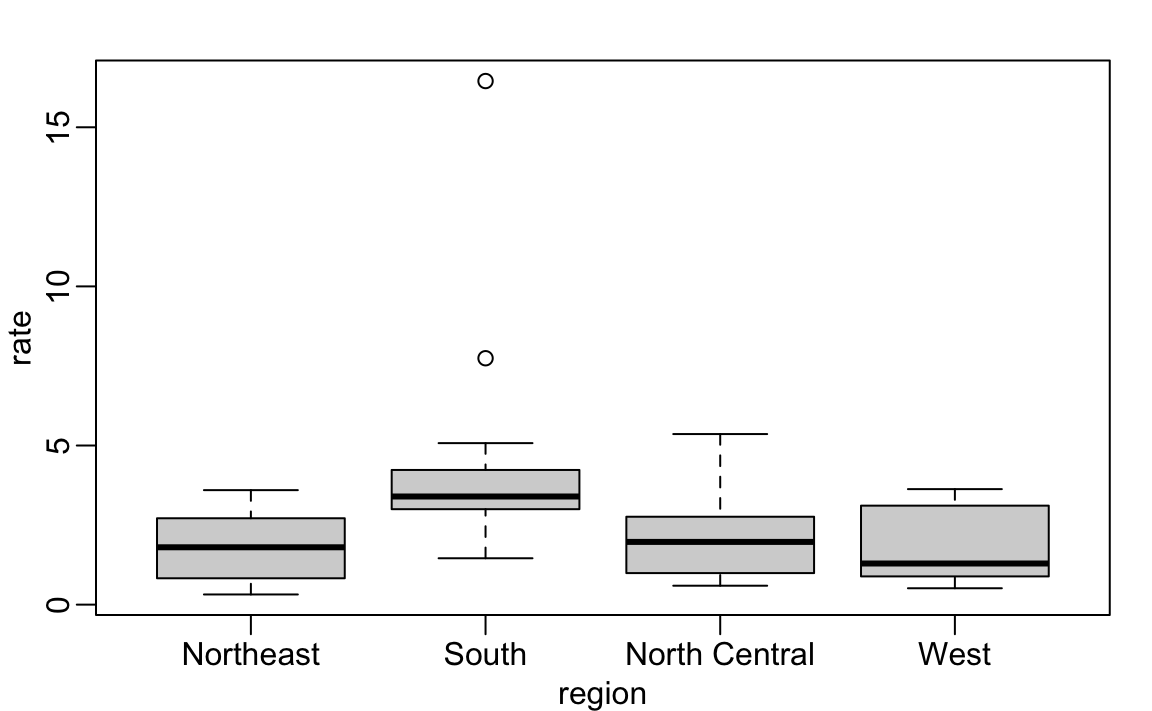

Podemos ver que el Sur (South en inglés) tiene tasas de asesinatos más altas que las otras tres regiones.

2.15.4 image

La función image muestra los valores en una matriz usando color. Aquí mostramos un ejemplo rápido:

x <- matrix(1:120, 12, 10)
image(x)

2.16 Ejercicios

1. Hicimos un gráfico de asesinatos totales versus población y notamos una fuerte relación. No es sorprendente que los estados con poblaciones más grandes hayan tenido más asesinatos.

library(dslabs)
data(murders)
population_in_millions <- murders$population/10^6
total_gun_murders <- murders$total
plot(population_in_millions, total_gun_murders)

Recuerden que muchos estados tienen poblaciones inferiores a 5 millones y están agrupados. Podemos obtener más información al hacer este gráfico en la escala logarítmica. Transforme las variables usando la transformación log10 y luego cree un gráfico de los resultados.

2. Cree un histograma de las poblaciones estatales.

3. Genere diagramas de caja de las poblaciones estatales por región.

---

11. https://rstudio.cloud↩︎

12. https://rafalab.github.io/dsbook/installing-r-rstudio.html↩︎

13. http://abcnews.go.com/blogs/headlines/2012/12/us-gun-ownership-homicide-rate-higher-than-other-developed-countries/↩︎

14. http://adv-r.had.co.nz/Style.html↩︎