Capítulo 19 La correlación no implica causalidad

La correlación no implica causalidad es quizás la lección más importante que uno aprende en una clase de estadística. A lo largo de la parte de estadísticas del libro, hemos descrito herramientas útiles para cuantificar asociaciones entre variables. Sin embargo, debemos tener cuidado de no malinterpretar estas asociaciones.

Hay muchas razones por las que una variable \(X\) se puede correlacionar con una variable \(Y\) sin tener ningún efecto directo sobre \(Y\). A continuación examinaremos cuatro formas comunes que pueden conducir a una malinterpretación de los datos.

19.1 Correlación espuria

El siguiente ejemplo cómico subraya que la correlación no es causalidad. Muestra una correlación muy fuerte entre las tasas de divorcio y el consumo de margarina.

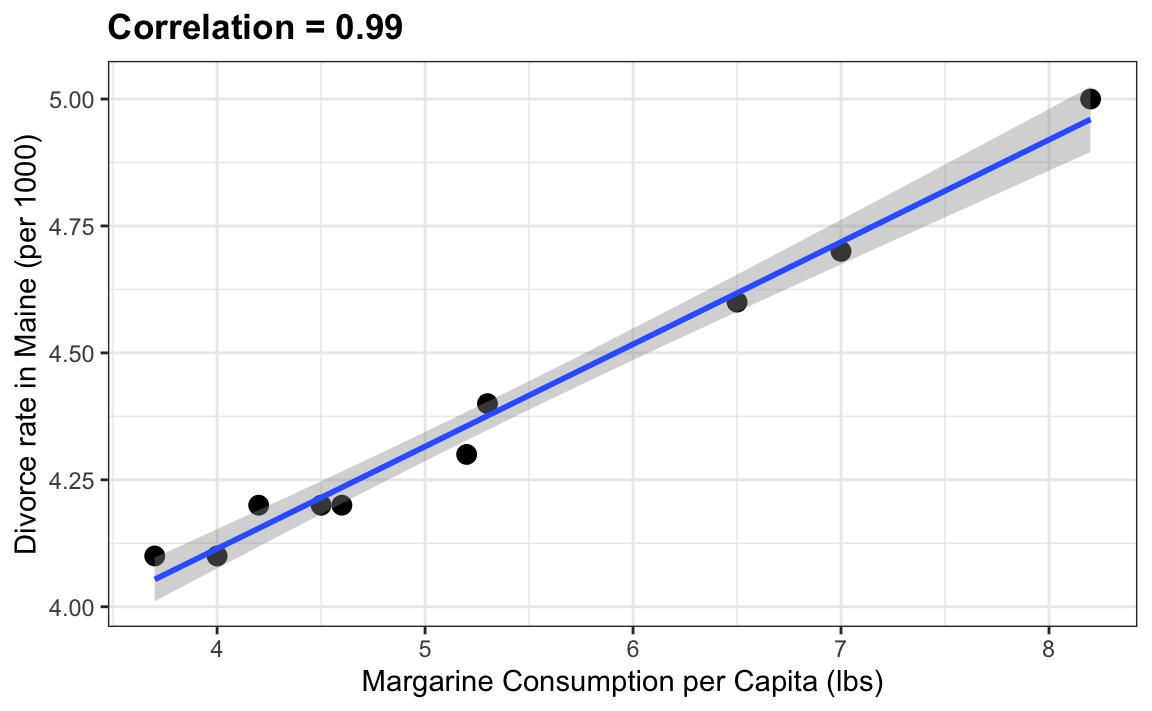
¿Significa esto que la margarina causa divorcios? ¿O los divorcios hacen que las personas coman más margarina? Por supuesto, la respuesta a ambas preguntas es “no”. Esto es solo un ejemplo de lo que llamamos una correlación espuria.

Pueden ver muchos más ejemplos absurdos en el sitio web Spurious Correlations⁸².

Los casos que se presentan en el sitio de web de correlaciones espurias son todas instancias de lo que generalmente se llama dragado de datos o pesca de datos (data dredging, data fishing, o data snooping en inglés). Básicamente es cuando se escogen los datos selectivamente para confirmar cierta hipótesis. Un ejemplo de dragado de datos sería si observamos muchos resultados producidos por un proceso aleatorio y elegimos solo los que muestran una relación que respalda una teoría que queremos defender.

Se puede usar una simulación Monte Carlo para mostrar cómo el dragado de datos puede resultar en altas correlaciones entre variables no correlacionadas. Guardaremos los resultados de nuestra simulación en un tibble:

N <- 25
g <- 1000000
sim_data <- tibble(group = rep(1:g, each=N),
                   x = rnorm(N * g),
                   y = rnorm(N * g))

La primera columna denota grupo. Creamos grupos y para cada uno generamos un par de vectores independientes, \(X\) e \(Y\), cada una con 25 observaciones, almacenadas en la segunda y tercera columnas. Debido a que construimos la simulación, sabemos que \(X\) e \(Y\) no están correlacionadas.

A continuación, calculamos la correlación entre \(X\) e \(Y\) para cada grupo y miramos el máximo:

res <- sim_data |>
  group_by(group) |>
  summarize(r = cor(x, y)) |>
  arrange(desc(r))
res
#> # A tibble: 1,000,000 × 2
#>    group     r
#>    <int> <dbl>
#> 1 158870 0.783
#> 2 424563 0.779
#> 3 691901 0.774
#> 4 931740 0.760
#> 5 579281 0.749
#> # … with 999,995 more rows

Vemos una correlación máxima de 0.783 y, si solo graficamos los datos del grupo con esta correlación, vemos un gráfico convincente que \(X\) e \(Y\) sí están correlacionados:

sim_data |> filter(group == res$group[which.max(res$r)]) |>
  ggplot(aes(x, y)) +
  geom_point() +
  geom_smooth(method = "lm")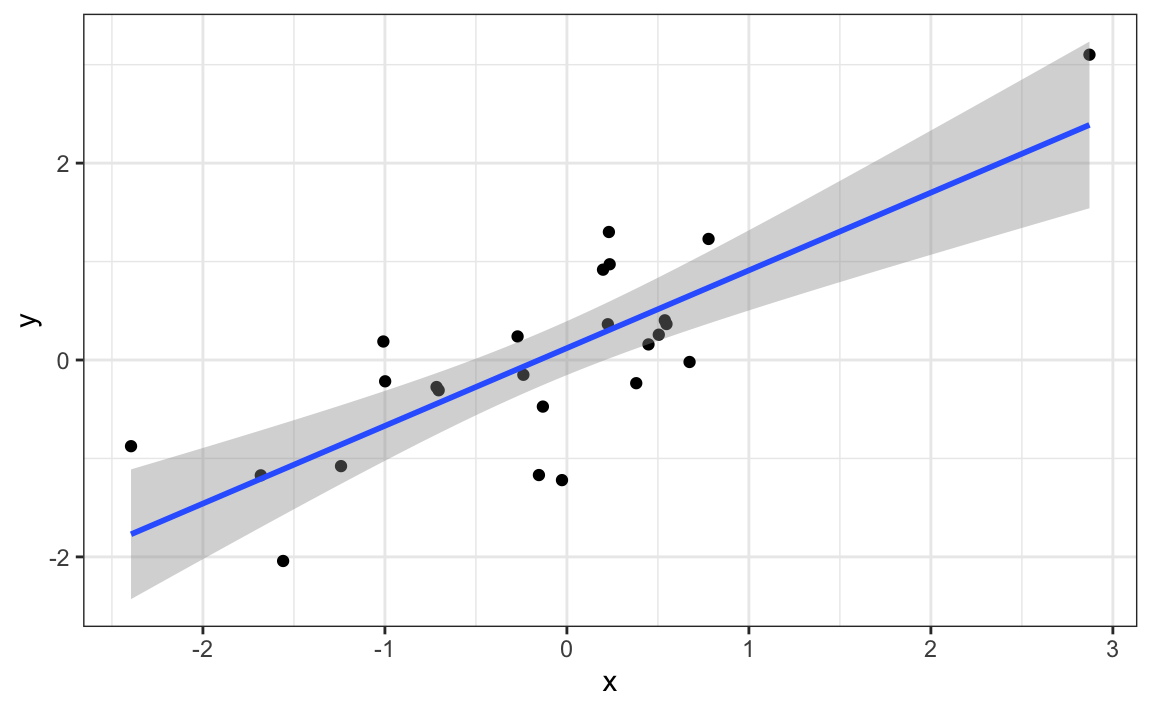

Recuerden que el resumen de correlación es una variable aleatoria. Aquí tenemos la distribución generada por la simulación Monte Carlo:

res |> ggplot(aes(x=r)) + geom_histogram(binwidth = 0.1, color = "black")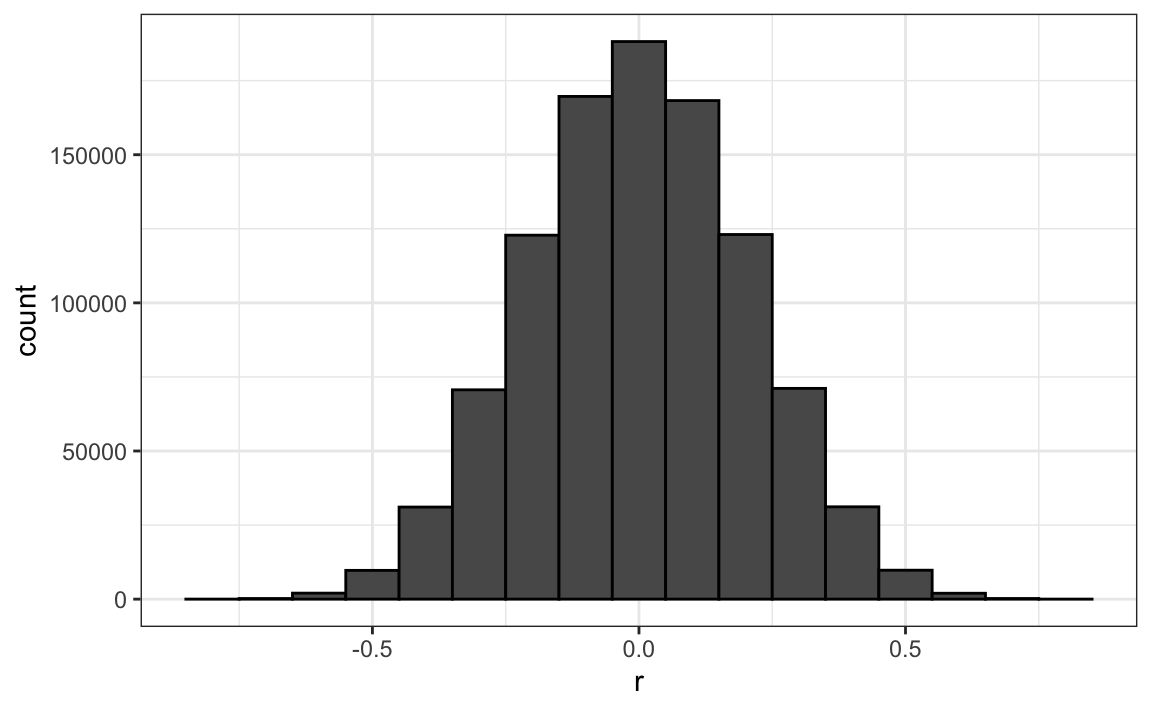

Es un hecho matemático que si observamos correlaciones aleatorias que se esperan que sean 0, pero tienen un error estándar de 0.204, la más grande estará cerca de 1.

Si realizamos una regresión en este grupo e interpretamos el valor-p, afirmaríamos incorrectamente que esta es una relación estadísticamente significativa:

library(broom)
sim_data |>
  filter(group == res$group[which.max(res$r)]) |>
  summarize(tidy(lm(y ~ x))) |>
  filter(term == "x")
#> # A tibble: 1 × 5
#>   term  estimate std.error statistic    p.value
#>   <chr>    <dbl>     <dbl>     <dbl>      <dbl>
#> 1 x         1.01     0.168      6.03 0.00000379

Esta forma particular de dragado de datos se conoce como p-hacking. El p-hacking es un tema de mucha discusión porque es un problema en publicaciones científicas. Debido a que los editores tienden a premiar resultados estadísticamente significativos sobre resultados negativos, existe un incentivo para informar resultados significativos. En la epidemiología y las ciencias sociales, por ejemplo, los investigadores pueden buscar asociaciones entre un resultado adverso y varias exposiciones a distintos tipos de riesgo e informar solo la exposición que resultó en un valor-p pequeño. Además, podrían intentar ajustar varios modelos diferentes para tomar en cuenta la confusión y elegir el que da el valor-p más pequeño. En disciplinas experimentales, un experimento puede repetirse más de una vez, pero solo informar los resultados del experimento con un valor-p pequeño. Esto no sucede necesariamente debido a comportamientos antiéticos, sino más bien como resultado de la ignorancia estadística o de meras ilusiones. En los cursos de estadística avanzada, pueden aprender métodos para tomar en cuenta estas múltiples comparaciones.

19.2 Valores atípicos

Supongan que tomamos medidas de dos resultados independientes, \(X\) e \(Y\), y estandarizamos las medidas. Sin embargo, cometemos un error y olvidamos estandarizar la entrada 23. Podemos simular dichos datos usando:

set.seed(1985)
x <- rnorm(100,100,1)
y <- rnorm(100,84,1)
x[-23] <- scale(x[-23])
y[-23] <- scale(y[-23])

Los datos se ven así:

qplot(x, y)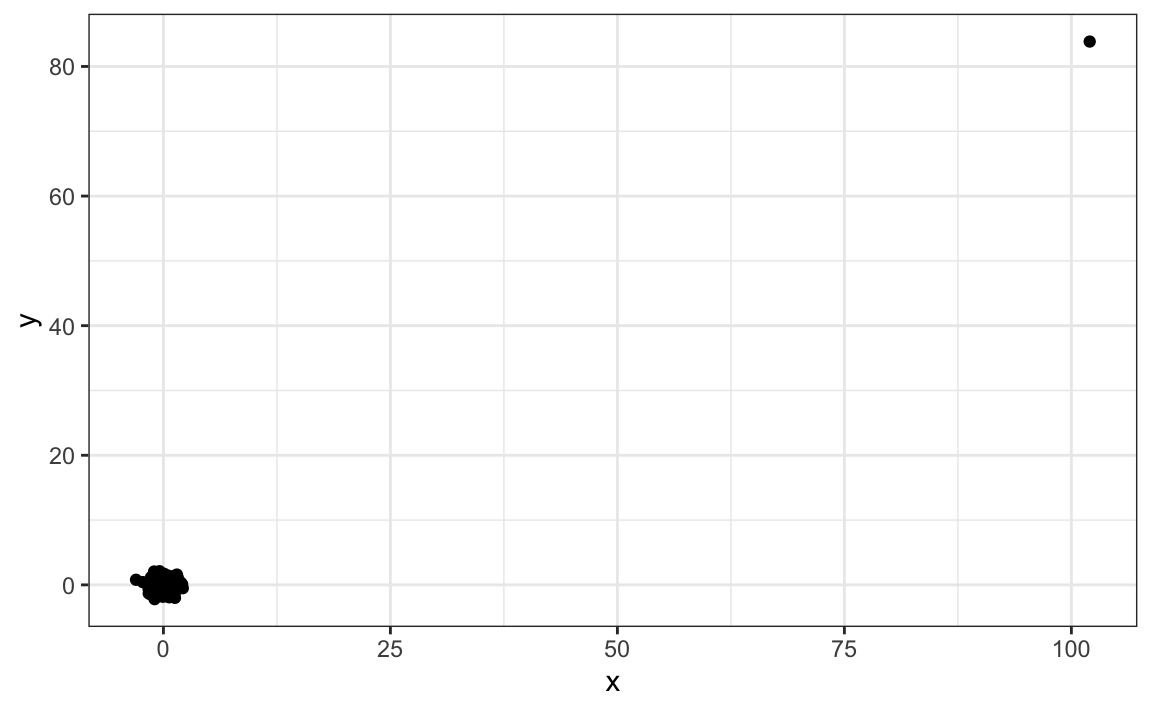

No es sorprendente que la correlación sea bien alta:

cor(x,y)
#> [1] 0.988

Pero lo impulsa un valor atípico. Si eliminamos este valor atípico, la correlación se reduce considerablemente a casi 0, que es lo que debería ser:

cor(x[-23], y[-23])
#> [1] -0.0442

En la Sección 11, describimos alternativas al promedio y la desviación estándar que son robustas a valores atípicos. También hay una alternativa a la correlación muestral para estimar la correlación de población que es robusta a valores atípicos. Se llama la correlación de Spearman. La idea es sencilla: calcular la correlación basada en los rangos de los valores. Aquí tenemos un gráfico de los rangos graficados uno contra el otro:

qplot(rank(x), rank(y))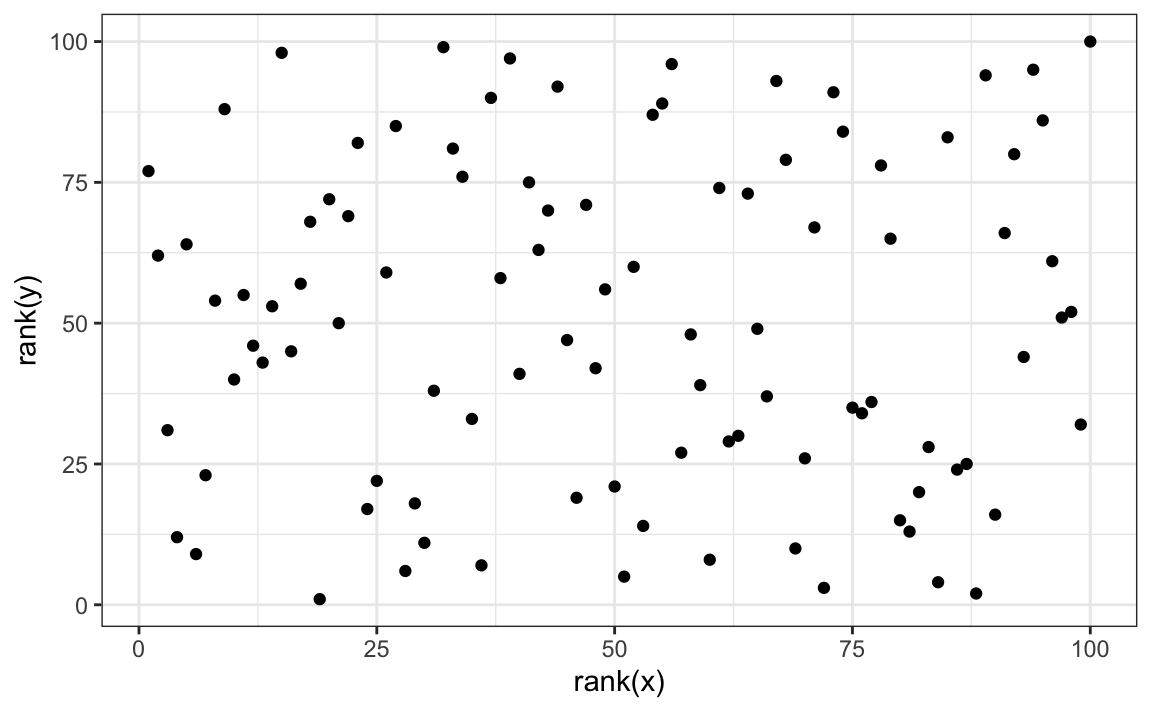

El valor atípico ya no está asociado con un valor muy grande y la correlación se reduce:

cor(rank(x), rank(y))
#> [1] 0.00251

La correlación de Spearman también se puede calcular así:

cor(x, y, method = "spearman")
#> [1] 0.00251

Además, hay métodos robustos para ajustar modelos lineales que pueden aprender, por ejemplo, en en libro Robust Statistics: Edition 2 de Peter J. Huber y Elvezio M. Ronchetti.

19.3 Inversión de causa y efecto

Otra forma en que la asociación se confunde con la causalidad es cuando la causa y el efecto se invierten. Un ejemplo de esto es afirmar que la tutoría afecta negativamente a los estudiantes porque éstos evalúan peor que sus compañeros que no reciben tutoría. En este caso, la tutoría no está causando las bajas puntuaciones en las pruebas, sino al revés.

Una versión de este reclamo se convirtió en un artículo de opinión en el New York Times titulado Parental Involvement Is Overrated⁸³. Consideren esta cita del artículo:

Cuando examinamos si la ayuda frecuente con la tarea tuvo un impacto positivo en el desempeño académico de los niños, nos sorprendió lo que encontramos. Independientemente de la clase social de la familia, del origen racial o étnico, o del grado de un niño, ayuda consistente con la tarea casi nunca mejoró la puntuación de las pruebas o las notas … Incluso más sorprendente para nosotros fue que cuando los padres ayudaban frecuentemente con la tarea, los niños generalmente salían peor.

Una posibilidad muy probable es que los niños que necesitan ayuda frecuente de sus padres reciban esta ayuda porque no se desempeñan bien en la escuela.

Fácilmente podemos construir un ejemplo de inversión de causa y efecto utilizando los datos de altura de padre e hijo. Si nos ajustamos al modelo:

\[X_i = \beta_0 + \beta_1 y_i + \varepsilon_i, i=1, \dots, N\]

a los datos de altura de padre e hijo, con \(X_i\) la altura del padre e \(y_i\) la altura del hijo, obtenemos un resultado estadísticamente significativo:

library(HistData)
data("GaltonFamilies")
GaltonFamilies |>
  filter(childNum == 1 & gender == "male") |>
  select(father, childHeight) |>
  rename(son = childHeight) |>
  summarize(tidy(lm(father ~ son)))
#>          term estimate std.error statistic  p.value
#> 1 (Intercept)   33.965    4.5682      7.44 4.31e-12
#> 2         son    0.499    0.0648      7.70 9.47e-13

El modelo se ajusta muy bien a los datos. Si observamos la formulación matemática del modelo anterior, podría interpretarse fácilmente de manera incorrecta para sugerir que el hijo siendo alto hace que el padre sea alto. Pero dado lo que sabemos sobre genética y biología, sabemos que es al revés. El modelo es técnicamente correcto. Los estimadores y los valores-p también se obtuvieron correctamente. Lo que está mal aquí es la interpretación.

19.4 Factores de confusión

Los factores de confusión son quizás la razón más común que conduce a que las asociaciones se malinterpreten.

Si \(X\) e \(Y\) están correlacionados, llamamos \(Z\) un factor de confusión (confounder en inglés) si cambios en \(Z\) provocan cambios en ambos \(X\) e \(Y\). Anteriormente, al estudiar los datos del béisbol, vimos cómo los cuadrangulares eran un factor de confusión que resultaban en una correlación más alta de lo esperado al estudiar la relación entre BB y HR. En algunos casos, podemos usar modelos lineales para tomar en cuenta los factores de confusión. Sin embargo, este no siempre es el caso.

La interpretación incorrecta debido a factores de confusión es omnipresente en la prensa laica y, a menudo, son difíciles de detectar. Aquí, presentamos un ejemplo ampliamente utilizado relacionado con las admisiones a la universidad.

19.4.1 Ejemplo: admisiones a la Universidad de California, Berkeley

Los datos de admisión de seis concentraciones de U.C. Berkeley, de 1973, mostraron que se admitían a más hombres que mujeres: el 44% de los hombres fueron aceptados en comparación con el 30% de las mujeres. PJ Bickel, EA Hammel & JW O’Connell. Science (1975). Podemos cargar los datos y ejecutar una prueba estadística, que rechaza claramente la hipótesis de que el género y la admisión son independientes:

data(admissions)
two_by_two <- admissions |> group_by(gender) |> 
  summarize(total_admitted = round(sum(admitted / 100 * applicants)), 
            not_admitted = sum(applicants) - sum(total_admitted)) |>
  select(-gender) 
  
chisq.test(two_by_two)$p.value
#> [1] 1.06e-21

Pero una inspección más cuidadosa muestra un resultado paradójico. Aquí están los porcentajes de admisión por concentración :

admissions |> select(major, gender, admitted) |>
  pivot_wider(names_from = "gender", values_from = "admitted") |>
  mutate(women_minus_men = women - men)
#> # A tibble: 6 × 4
#>   major   men women women_minus_men
#>   <chr> <dbl> <dbl>           <dbl>
#> 1 A        62    82              20
#> 2 B        63    68               5
#> 3 C        37    34              -3
#> 4 D        33    35               2
#> 5 E        28    24              -4
#> # … with 1 more row

Cuatro de las seis concentraciones favorecen a las mujeres. Más importante aún, todas las diferencias son mucho más pequeñas que la diferencia de 14.2 que vemos al examinar los totales.

La paradoja es que analizar los totales sugiere una dependencia entre admisión y género, pero cuando los datos se agrupan por concentración, esta dependencia parece desaparecer. ¿Qué está pasando? Esto puede suceder cuando un factor de confusión no detectado está impulsando la mayor parte de la variabilidad.

Así que definamos tres variables: \(X\) es 1 para hombres y 0 para mujeres, \(Y\) es 1 para los admitidos y 0 en caso contrario, y \(Z\) cuantifica la selectividad de la concentración. Una afirmación de sesgo de género se basaría en el hecho de que \(\mbox{Pr}(Y=1 | X = x)\) es mayor para \(x=1\) que \(x=0\). Sin embargo, \(Z\) es un factor de confusión importante para tomar en cuenta. Claramente \(Z\) está asociado con \(Y\), ya que entre más selectiva sea la concentración, \(\mbox{Pr}(Y=1 | Z = z)\) será menor. Pero, ¿está asociada la selección de concentración \(Z\) con el género \(X\)?

Una forma de ver esto es graficar el porcentaje total admitido a una concentración versus el porcentaje de mujeres que componen los solicitantes:

admissions |>
  group_by(major) |>
  summarize(major_selectivity = sum(admitted * applicants)/sum(applicants),
            percent_women_applicants = sum(applicants * (gender=="women"))/
              sum(applicants) * 100) |>
  ggplot(aes(major_selectivity, percent_women_applicants, label = major)) +
  geom_text()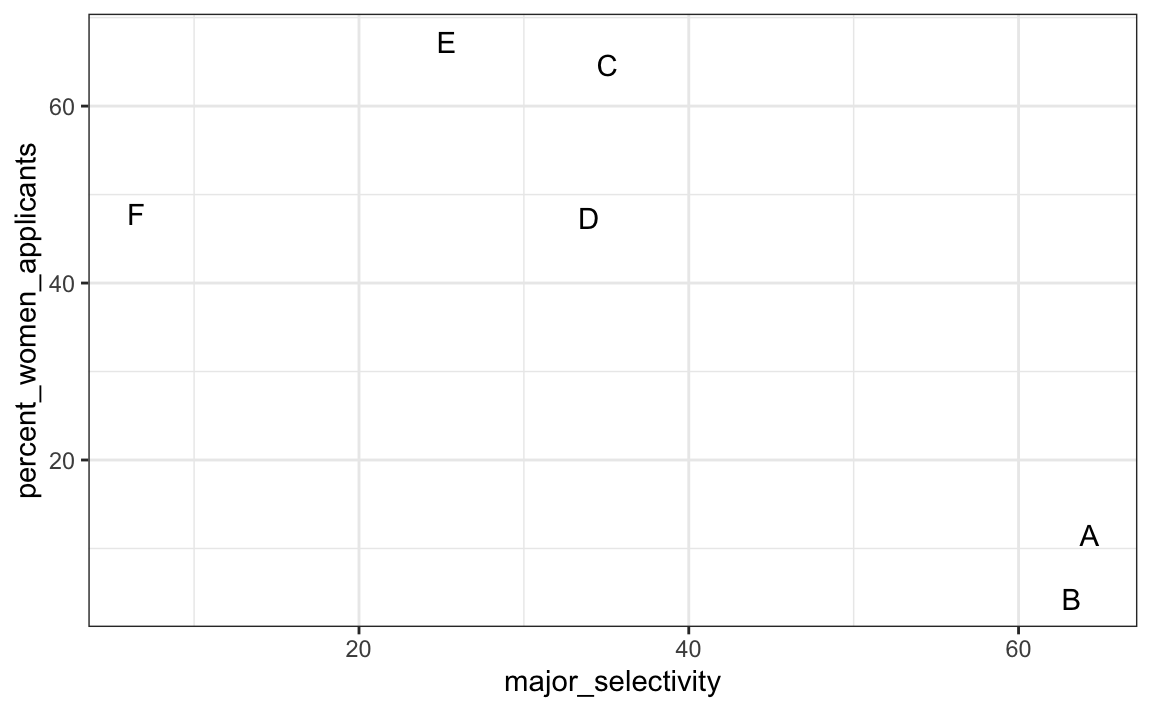

Parece haber asociación. El gráfico sugiere que las mujeres eran mucho más propensas a solicitar a las dos concentraciones “difíciles”: el género y la selectividad de la concentración están confundidos. Compare, por ejemplo, la concentración B y la E. La concentración B es mucho más difícil de ingresar que la B y más del 60% de los solicitantes a la concentración E eran mujeres, mientras que menos del 30% de los solicitantes a la concentración B eran mujeres.

19.4.2 Confusión explicada gráficamente

El siguiente gráfico muestra el número de solicitantes que fueron admitidos y los que no fueron según sexo:

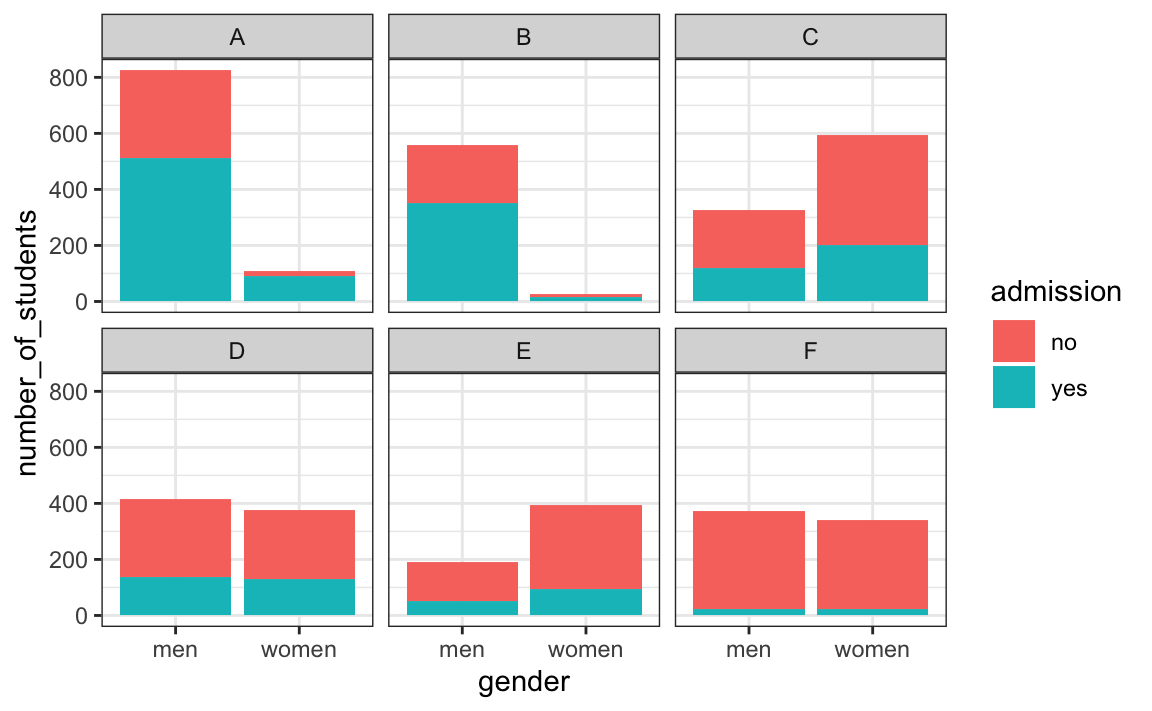
También desglosamos las aceptaciones por concentración. Este gráfico nos permite ver que la mayoría de los hombres aceptados provenían de dos concentraciones: A y B, y que pocas mujeres solicitaron estas concentraciones.

19.4.3 Calcular promedio luego de estratificar

En este gráfico, podemos ver que si condicionamos o estratificamos por concentración, controlamos el factor de confusión y este efecto desaparece:

admissions |>
  ggplot(aes(major, admitted, col = gender, size = applicants)) +
  geom_point()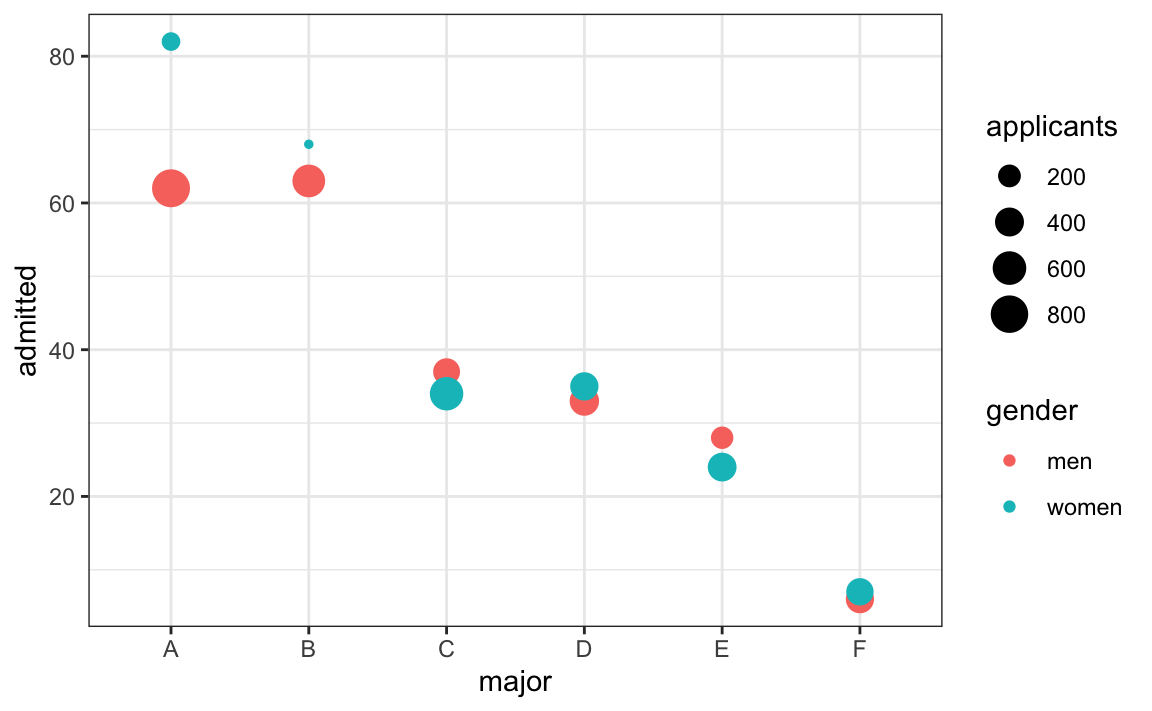

Ahora vemos que concentración por concentración, no hay mucha diferencia. El tamaño del punto representa el número de solicitantes y explica la paradoja: vemos grandes puntos rojos y pequeños puntos azules para las concentraciones más fáciles/menos retantes, A y B.

Si promediamos la diferencia por concentración, encontramos que el porcentaje es 3.5% más alto para las mujeres.

admissions |> group_by(gender) |> summarize(average = mean(admitted))
#> # A tibble: 2 × 2
#>   gender average
#>   <chr>    <dbl>
#> 1 men       38.2
#> 2 women     41.7

19.5 La paradoja de Simpson

El caso que acabamos de discutir es un ejemplo de la paradoja de Simpson. Se le llama paradoja porque vemos que el signo de la correlación cambia al comparar la población entera y estratos específicos. Como ejemplo ilustrativo, supongan que observamos realizaciones de las tres variables aleatorias \(X\), \(Y\) y \(Z\). Aquí hay un gráfico de observaciones simuladas para \(X\) e \(Y\) junto con la correlación de muestra:

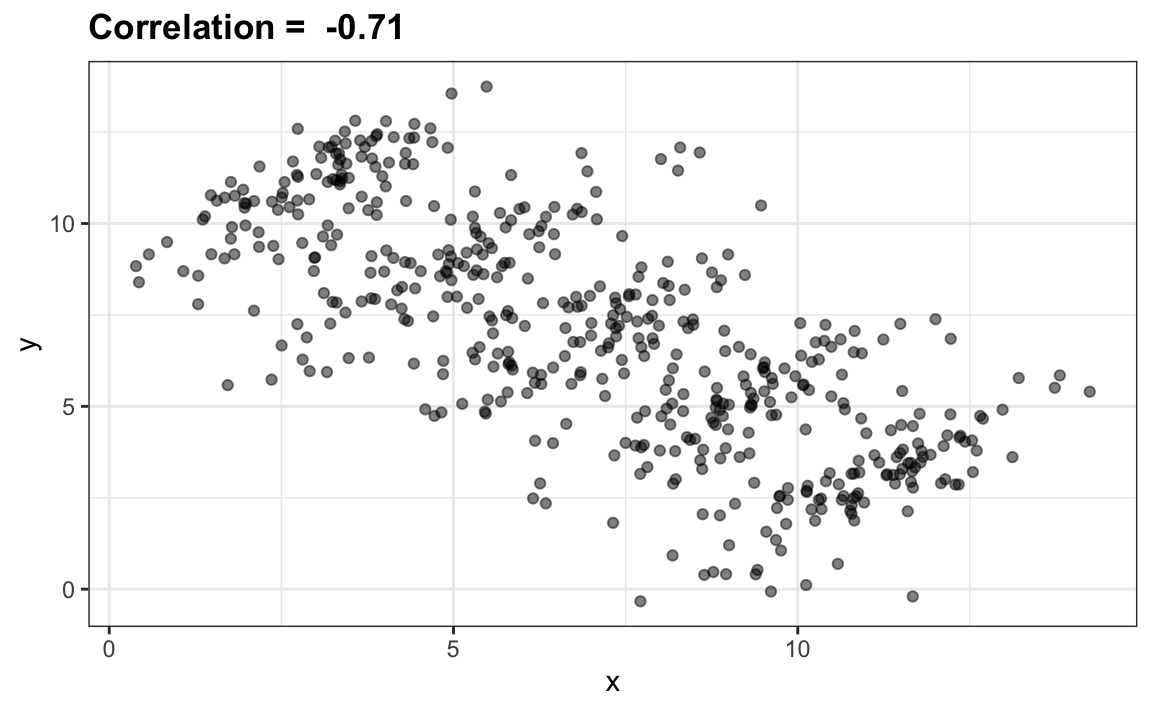
Pueden ver que \(X\) e \(Y\) están correlacionados negativamente. Sin embargo, una vez que estratificamos por \(Z\) (se muestra en diferentes colores a continuación), surge otro patrón:

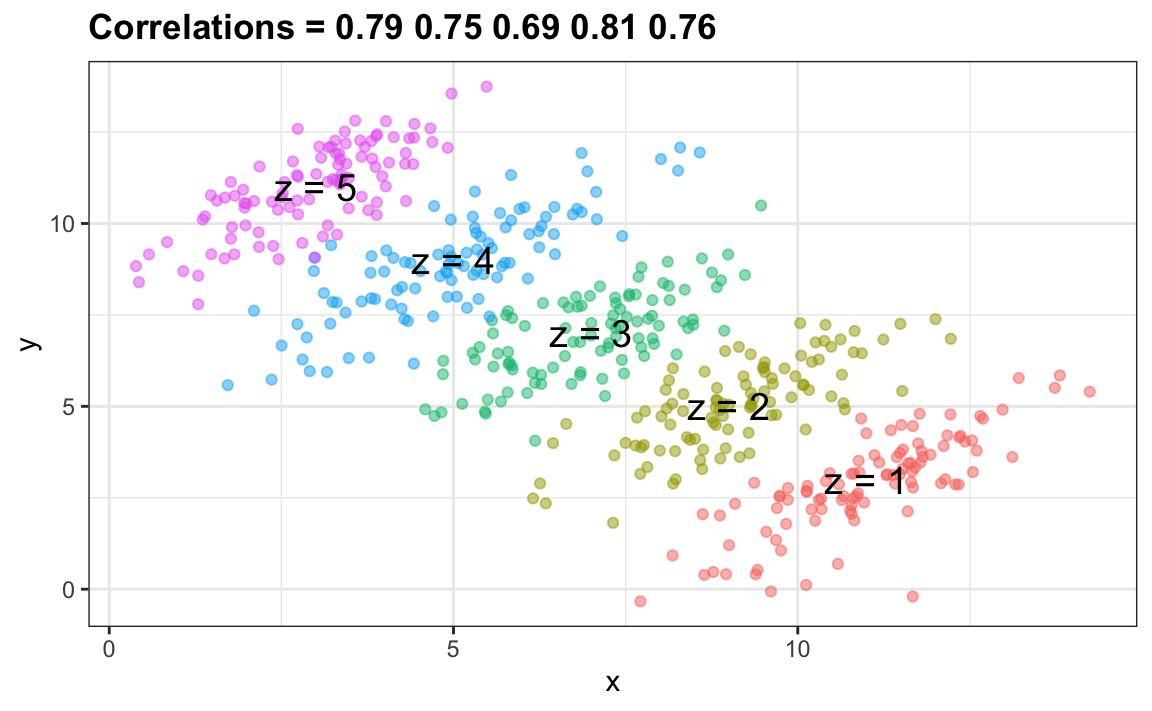
Realmente es \(Z\) que está negativamente correlacionada con \(X\). Si estratificamos por \(Z\), las \(X\) e \(Y\) están positivamente correlacionadas como se observa en el gráfico anterior.

19.6 Ejercicios

Para el próximo set de ejercicios, examinamos los datos de un artículo de PNAS del 2014⁸⁴ que analizó las tasas de éxito de agencias de financiación en los Países Bajos y concluyó que:

Nuestros resultados revelan un sesgo de género que favorece a los solicitantes sobre las solicitantes en la priorización de sus evaluaciones y tasas de éxito con respecto a su “calidad de investigador” (pero no “calidad de propuesta”), así como en el lenguaje utilizado en los materiales de instrucción y evaluación.

Unos meses después, se publicó una respuesta⁸⁵ titulada No evidence that gender contributes to personal research funding success in The Netherlands: A reaction to Van der Lee and Ellemers que concluyó:

Sin embargo, el efecto general del género apenas alcanza significancia estadística, a pesar del tamaño grande de la muestra. Además, su conclusión podría ser un excelente ejemplo de la paradoja de Simpson; si un mayor porcentaje de mujeres solicita subvenciones en disciplinas científicas más competitivas (es decir, con bajas tasas de éxito de solicitudes tanto para hombres como para mujeres), entonces un análisis de todas las disciplinas podría mostrar incorrectamente “evidencia” de desigualdad de género.

¿Quién tiene la razón aquí? ¿El artículo original o la respuesta? Aquí, examinarán los datos y llegarán a su propia conclusión.

1. La evidencia principal para la conclusión del artículo original se reduce a una comparación de los porcentajes. La Tabla S1 en el artículo incluye la información que necesitamos:

library(dslabs)
data("research_funding_rates")
research_funding_rates

Construya la tabla 2 X 2 utilizada para la conclusión sobre las diferencias en los premios por género.

2. Calcule la diferencia en porcentaje de la tabla 2 X 2.

3. En el ejercicio anterior, notamos que la tasa de éxito es menor para las mujeres. ¿Pero es significativo? Calcule un valor-p usando una prueba de Chi-cuadrado.

4. Vemos que el valor-p es aproximadamente 0.05. Entonces parece haber algo de evidencia de una asociación. ¿Pero podemos inferir causalidad aquí? ¿El sesgo de género está causando esta diferencia observada? La respuesta al artículo original afirma que lo que vemos aquí es similar al ejemplo de las admisiones a U.C. Berkeley. Para resolver esta disputa, cree un set de datos con el número de solicitudes, premios y tasas de éxito para cada género. Reordene las disciplinas por su tasa de éxito general. Sugerencia: use la función reorder para reordenar las disciplinas como primer paso, luego use pivot_longer, separate y pivot_wider para crear la tabla deseada.

5. Para verificar si este es un caso de la paradoja de Simpson, grafique las tasas de éxito versus las disciplinas, que han sido ordenadas según éxito general, con colores para denotar los géneros y tamaño para denotar el número de solicitudes.

6. Definitivamente no vemos el mismo nivel de confusión que en el ejemplo de U.C. Berkeley. Es difícil decir que hay un factor de confusión aquí. Sin embargo, vemos que, según las tasas observadas, algunos campos favorecen a los hombres y otros favorecen a las mujeres. Además, vemos que los dos campos con la mayor diferencia que favorecen a los hombres también son los campos con más solicitudes. Pero, a diferencia del ejemplo de U.C. Berkeley, no es más probable que las mujeres soliciten las concentraciones más difíciles. Entonces, quizás algunos de los comités de selección son parciales y otros no.

Pero, antes de concluir esto, debemos verificar si estas diferencias son diferentes de lo que obtenemos por casualidad. ¿Alguna de las diferencias vistas anteriormente es estadísticamente significativa? Tengan en cuenta que incluso cuando no hay sesgo, veremos diferencias debido a la variabilidad aleatoria en el proceso de revisión, así como entre los candidatos. Realice una prueba de Chi-cuadrado para cada disciplina. Sugerencia: defina una función que reciba el total de una tabla 2 X 2 y devuelva un data frame con el valor-p. Use la corrección 0.5. Luego use la función summarize.

7. Para las ciencias médicas, parece haber una diferencia estadísticamente significativa. ¿Pero es esto una correlación espuria? Realice 9 pruebas. Informar solo el caso con un valor-p inferior a 0.05 podría considerarse un ejemplo de dragado de datos. Repita el ejercicio anterior, pero en lugar de un valor-p, calcule un logaritmo de riesgo relativo (log odds ratio en inglés) dividido por su error estándar. Entonces use un gráfico Q-Q para ver cuánto se desvían estos logaritmos de riesgo relativo de la distribución normal que esperaríamos: una distribución normal estándar.

---

82. http://tylervigen.com/spurious-correlations↩︎

83. https://opinionator.blogs.nytimes.com/2014/04/12/parental-involvement-is-overrated↩︎

84. http://www.pnas.org/content/112/40/12349.abstract↩︎

85. http://www.pnas.org/content/112/51/E7036.extract↩︎