Capítulo 11 Resúmenes robustos
11.1 Valores atípicos
Anteriormente describimos cómo los diagramas de caja muestran valores atípicos (outliers en inglés), pero no ofrecimos una definición precisa. Aquí discutimos los valores atípicos, los acercamientos que pueden ayudar para detectarlos y los resúmenes que toman en cuenta su presencia.
Los valores atípicos son muy comunes en la ciencia de datos. La recopilación de datos puede ser compleja y es común observar puntos de datos generados por error. Por ejemplo, un viejo dispositivo de monitoreo puede leer mediciones sin sentido antes de fallar por completo. El error humano también es una fuente de valores atípicos, en particular cuando la entrada de datos se realiza manualmente. Un individuo, por ejemplo, puede ingresar erróneamente su altura en centímetros en lugar de pulgadas o colocar el decimal en el lugar equivocado.
¿Cómo distinguimos un valor atípico de mediciones que son demasiado grandes o pequeñas simplemente debido a la variabilidad esperada? Esta no siempre es una pregunta fácil de contestar, pero intentaremos ofrecer alguna orientación. Comencemos con un caso sencillo.
Supongan que un colega se encarga de recopilar datos demográficos para un grupo de varones. Los datos indican la altura en pies y se almacenan en el objeto:
library(tidyverse)
library(dslabs)
data(outlier_example)
str(outlier_example)
#> num [1:500] 5.59 5.8 5.54 6.15 5.83 5.54 5.87 5.93 5.89 5.67 ...Nuestro colega utiliza el hecho de que las alturas suelen estar bien aproximadas por una distribución normal y resume los datos con el promedio y la desviación estándar:
mean(outlier_example)
#> [1] 6.1
sd(outlier_example)
#> [1] 7.8y escribe un informe sobre el hecho interesante de que este grupo de varones es mucho más alto de lo normal. ¡La altura promedio es más de seis pies! Sin embargo, al usar sus conocimientos de ciencia de datos, notan algo más que es inesperado: la desviación estándar es de más de 7 pies. Al sumar y restar dos desviaciones estándar, observan que el 95% de esta población parece tener alturas entre -9.489, 21.697 pies, que no tiene sentido. Un gráfico rápido muestra el problema:
boxplot(outlier_example)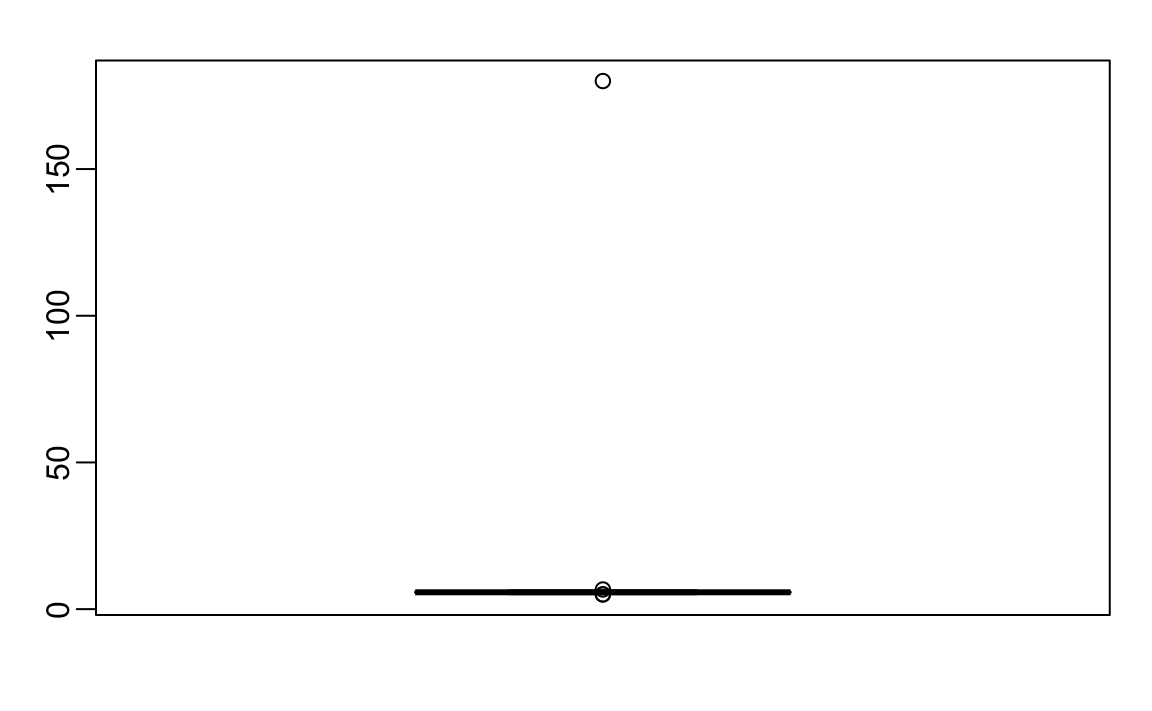
Parece que hay al menos un valor que no tiene sentido, ya que sabemos que una altura de 180 pies es imposible. El diagrama de caja detecta este punto como un valor atípico.
11.2 Mediana
Cuando tenemos un valor atípico como este, el promedio puede llegar a ser muy grande. Matemáticamente, podemos hacer que el promedio sea tan grande como queramos simplemente cambiando un número: con 500 puntos de datos, podemos aumentar el promedio en cualquier cantidad \(\Delta\) añadiendo \(\Delta \times\) 500 a un solo número. La mediana, definida como el valor para el cual la mitad de los valores son más pequeños y la otra mitad son más grandes, es robusta para tales valores atípicos. No importa cuán grande hagamos el punto más grande, la mediana sigue siendo la misma.
Con estos datos, la mediana es:
median(outlier_example)
#> [1] 5.74lo cual es aproximadamente 5 pies y 9 pulgadas.
La mediana es lo que los diagramas de caja muestran como una línea horizontal.
11.3 El rango intercuartil (IQR)
La caja en un diagrama de caja se define por el primer y tercer cuartil. Estos están destinados a proveer una idea de la variabilidad en los datos: el 50% de los datos están dentro de este rango. La diferencia entre el 3er y 1er cuartil (o los percentiles 75 y 25) se conoce como el rango intercuartil (IQR por sus siglas en inglés). Como sucede con la mediana, esta cantidad será robusta para los valores atípicos ya que los valores grandes no la afectan. Podemos hacer algunos cálculos y ver que para los datos que siguen la distribución normal, el IQR/1.349 se aproxima a la desviación estándar de los datos si un valor atípico no hubiera estado presente. Podemos ver que esto funciona bien en nuestro ejemplo, ya que obtenemos un estimado de la desviación estándar de:
IQR(outlier_example)/ 1.349
#> [1] 0.245lo cual es cerca de 3 pulgadas.
11.4 La definición de Tukey de un valor atípico
En R, los puntos que caen fuera de los bigotes del diagrama de caja se denominan valores atípicos, una definición que Tukey introdujo. El bigote superior termina en el percentil 75 más 1.5 \(\times\) IQR, mientras que el bigote inferior termina en el percentil 25 menos 1.5 \(\times\) IQR. Si definimos el primer y el tercer cuartil como \(Q_1\) y \(Q_3\), respectivamente, entonces un valor atípico es cualquier valor fuera del rango:
\[[Q_1 - 1.5 \times (Q_3 - Q1), Q_3 + 1.5 \times (Q_3 - Q1)].\]
Cuando los datos se distribuyen normalmente, las unidades estándar de estos valores son:
q3 <- qnorm(0.75)
q1 <- qnorm(0.25)
iqr <- q3 - q1
r <- c(q1 - 1.5*iqr, q3 + 1.5*iqr)
r
#> [1] -2.7 2.7Utilizando la función pnorm, vemos que 99.3% de los datos caen en este intervalo.
Tengan en cuenta que este no es un evento tan extremo: si tenemos 1000 puntos de datos que se distribuyen normalmente, esperamos ver unos 7 fuera de este rango. Pero estos no serían valores atípicos ya que esperamos verlos bajo la variación típica.
Si queremos que un valor atípico sea más raro, podemos cambiar el 1.5 a un número mas grande. Tukey también usó 3 y los denominó far out outliers o valores atípicos extremos. Con una distribución normal,
100%
de los datos caen en este intervalo. Esto se traduce en aproximadamente 2 en un millón de posibilidades de estar fuera del rango. En la función geom_boxplot, esto se puede controlar usando el argumento outlier.size, que por defecto es 1.5.
La medida de 180 pulgadas está más allá del rango de los datos de altura:
max_height <- quantile(outlier_example, 0.75) + 3*IQR(outlier_example)
max_height
#> 75%
#> 6.91Si sacamos este valor, podemos ver que los datos se distribuyen normalmente como se espera:
x <- outlier_example[outlier_example < max_height]
qqnorm(x)
qqline(x)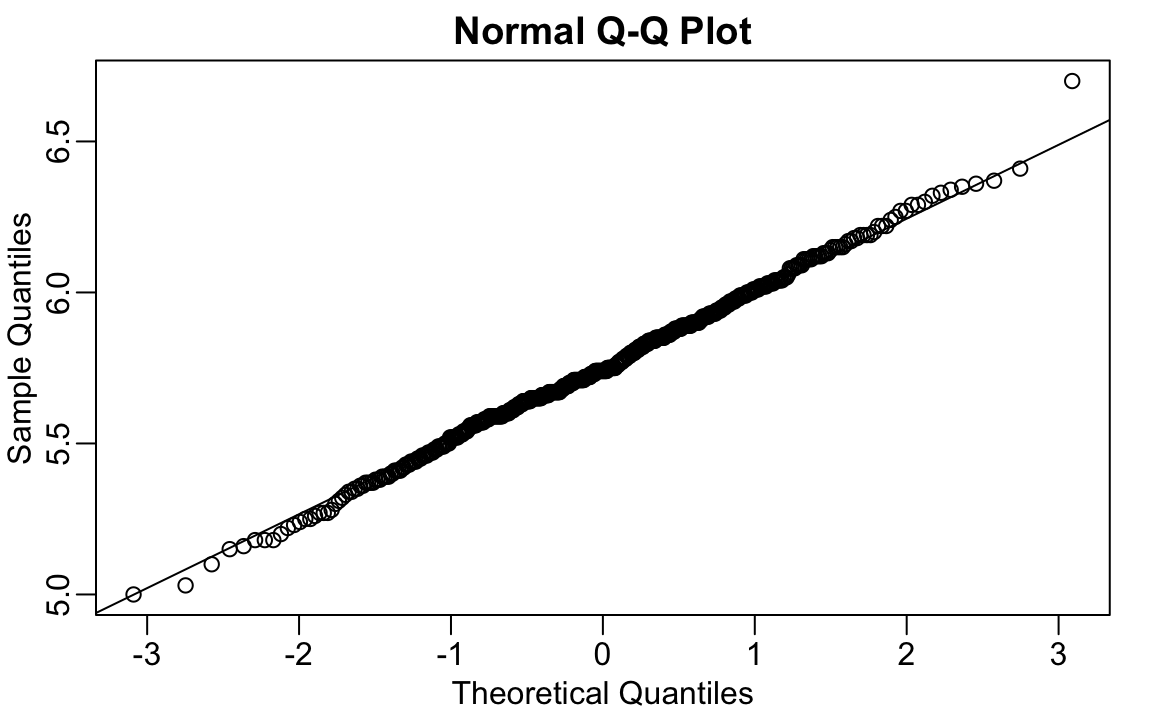
11.5 Desviación absoluta mediana
Otra opción para estimar la desviación estándar de manera robusta en presencia de valores atípicos es usar la desviación absoluta mediana (median absolute deviation o MAD por sus siglas en inglés). Para calcular el MAD, primero calculamos la mediana y luego, para cada valor, calculamos la distancia entre ese valor y la mediana. El MAD se define como la mediana de estas distancias. Por razones técnicas que no discutimos aquí, esta cantidad debe multiplicarse por 1.4826 para asegurar que se aproxime a la desviación estándar real. La función mad ya incorpora esta corrección. Para los datos de altura, obtenemos una MAD de:
mad(outlier_example)
#> [1] 0.237lo cual es cerca de 3 pulgadas.
11.6 Ejercicios
Vamos a usar el paquete HistData. Si no lo ha instalando, puede hacerlo así:
install.packages("HistData")Cargue el set de datos de altura y cree un vector x que contiene solo las alturas masculinas de los datos de Galton de los padres y sus hijos de su investigación histórica sobre la herencia.
library(HistData)
data(Galton)
x <- Galton$child1. Calcule el promedio y la mediana de estos datos.
2. Calcule la mediana y el MAD de estos datos.
3. Ahora supongan que Galton cometió un error al ingresar el primer valor y olvidó usar el punto decimal. Puede imitar este error escribriendo:
x_with_error <- x
x_with_error[1] <- x_with_error[1]*10¿Cuántas pulgadas crece el promedio como resultado de este error?
4. ¿Cuántas pulgadas crece la SD como resultado de este error?
5. ¿Cuántas pulgadas crece la mediana como resultado de este error?
6. ¿Cuántas pulgadas crece el MAD como resultado de este error?
7. ¿Cómo podríamos utilizar el análisis exploratorio de datos para detectar que se cometió un error?
- Dado que es solo un valor entre muchos, no se puede detectar esto.
- Veríamos un cambio obvio en la distribución.
- Un diagrama de caja, histograma o gráfico Q-Q revelarían un valor atípico obvio.
- Un diagrama de dispersión mostraría altos niveles de error de medición.
8. ¿Cuánto puede crecer accidentalmente el promedio con errores como este? Escribe una función llamada error_avg que toma un valor k y devuelve el promedio del vector x después de que la primera entrada cambie a k. Muestre los resultados para k=10000 y k=-10000.
11.7 Estudio de caso: alturas autoreportadas de estudiantes
Las alturas que hemos estado estudiando no son las alturas originales reportadas por los estudiantes. Las alturas originales también se incluyen en el paquete dslabs y se pueden cargar así:
library(dslabs)
data("reported_heights")La altura es un vector de caracteres, por lo que creamos una nueva columna con la versión numérica:
reported_heights <- reported_heights |>
mutate(original_heights = height, height = as.numeric(height))
#> Warning in mask$eval_all_mutate(quo): NAs introducidos por coerciónTengan en cuenta que recibimos una advertencia sobre los NAs. Esto se debe a que algunas de las alturas autoreportadas no eran números. Podemos ver por qué obtenemos estos NAs:
reported_heights |> filter(is.na(height)) |> head()
#> time_stamp sex height original_heights
#> 1 2014-09-02 15:16:28 Male NA 5' 4"
#> 2 2014-09-02 15:16:37 Female NA 165cm
#> 3 2014-09-02 15:16:52 Male NA 5'7
#> 4 2014-09-02 15:16:56 Male NA >9000
#> 5 2014-09-02 15:16:56 Male NA 5'7"
#> 6 2014-09-02 15:17:09 Female NA 5'3"Algunos estudiantes indicaron sus alturas usando pies y pulgadas en lugar de solo pulgadas. Otros usaron centímetros y otros solo estaban “trolleando”. Por ahora eliminaremos estas entradas:
reported_heights <- filter(reported_heights, !is.na(height))Si calculamos el promedio y la desviación estándar, observamos que obtenemos resultados extraños. El promedio y la desviación estándar son diferentes de la mediana y del MAD:
reported_heights |>
group_by(sex) |>
summarize(average = mean(height), sd = sd(height),
median = median(height), MAD = mad(height))
#> # A tibble: 2 × 5
#> sex average sd median MAD
#> <chr> <dbl> <dbl> <dbl> <dbl>
#> 1 Female 63.4 27.9 64.2 4.05
#> 2 Male 103. 530. 70 4.45Esto sugiere que tenemos valores atípicos, lo que se confirma creando un diagrama de caja:
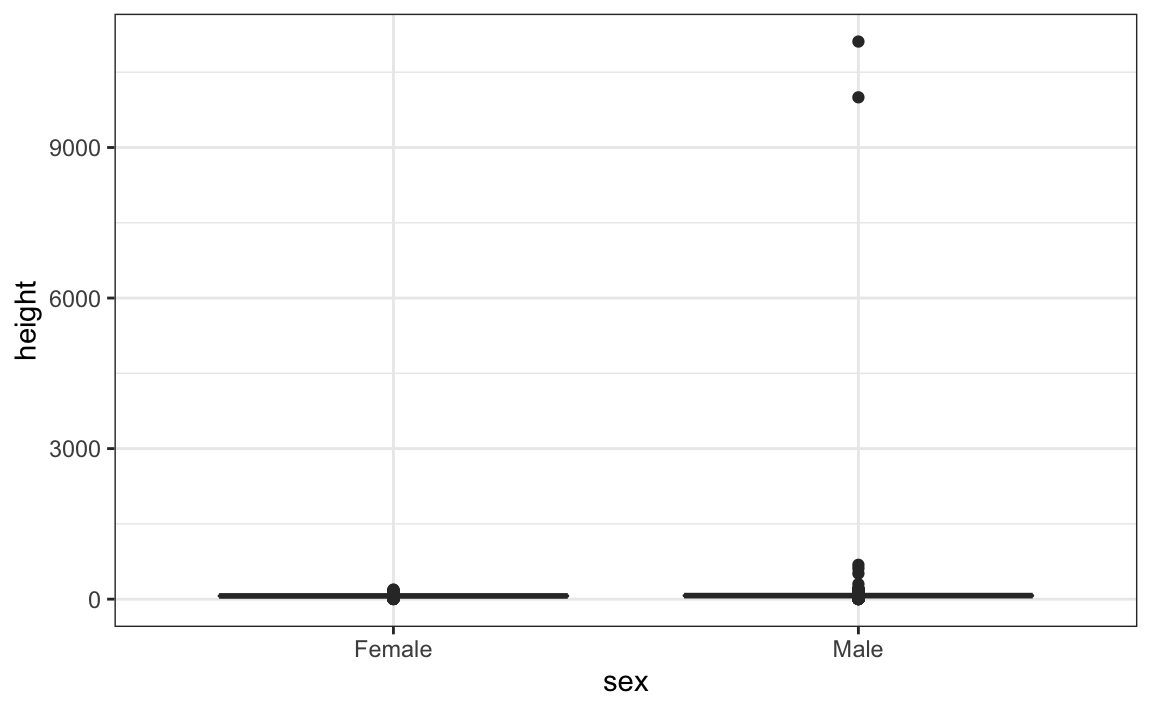
Vemos algunos valores bastante extremos. Para ver cuáles son estos valores, podemos rápidamente mirar los valores más grandes utilizando la función arrange:
reported_heights |> arrange(desc(height)) |> top_n(10, height)
#> time_stamp sex height original_heights
#> 1 2014-09-03 23:55:37 Male 11111 11111
#> 2 2016-04-10 22:45:49 Male 10000 10000
#> 3 2015-08-10 03:10:01 Male 684 684
#> 4 2015-02-27 18:05:06 Male 612 612
#> 5 2014-09-02 15:16:41 Male 511 511
#> 6 2014-09-07 20:53:43 Male 300 300
#> 7 2014-11-28 12:18:40 Male 214 214
#> 8 2017-04-03 16:16:57 Male 210 210
#> 9 2015-11-24 10:39:45 Male 192 192
#> 10 2014-12-26 10:00:12 Male 190 190
#> 11 2016-11-06 10:21:02 Female 190 190Las primeras siete entradas parecen errores extraños. Sin embargo, las siguientes entradas parecen haber sido ingresadas en centímetros en lugar de pulgadas. Dado que 184cm es equivalente a seis pies de altura, sospechamos que 184 realmente significa 72 pulgadas.
Podemos revisar todas las respuestas sin sentido examinando los datos que Tukey considera far out o extremos:
whisker <- 3*IQR(reported_heights$height)
max_height <- quantile(reported_heights$height, .75) + whisker
min_height <- quantile(reported_heights$height, .25) - whisker
reported_heights |>
filter(!between(height, min_height, max_height)) |>
select(original_heights) |>
head(n=10) |> pull(original_heights)
#> [1] "6" "5.3" "511" "6" "2" "5.25" "5.5" "11111"
#> [9] "6" "6.5"Al revisar estas alturas cuidadosamente, vemos dos errores comunes: entradas en centímetros, que resultan ser demasiado grandes, y entradas del tipo x.y con x e y representando pies y pulgadas respectivamente, que resultan ser demasiado pequeñas. Algunos de los valores aún más pequeños, como 1.6, podrían ser entradas en metros.
En la parte de wrangling de datos de este libro, aprenderemos técnicas para corregir estos valores y convertirlos en pulgadas. Aquí pudimos detectar este problema mediante una cuidadosa exploración de los datos para descubrir problemas con ellos: el primer paso en la gran mayoría de los proyectos de ciencia de datos.