Capítulo 33 Sets grandes de datos

Los problemas de machine learning a menudo implican sets de datos que son tan o más grandes que el set de datos MNIST. Existe una variedad de técnicas computacionales y conceptos estadísticos que son útiles para análisis de grandes sets de datos. En este capítulo, exploramos brevemente estas técnicas y conceptos al describir álgebra matricial, reducción de dimensiones, regularización y factorización de matrices. Utilizamos sistemas de recomendación relacionados con las clasificaciones de películas como un ejemplo motivador.

33.1 Álgebra matricial

En machine learning, las situaciones en las que todos los predictores son numéricos, o pueden representarse como números son comunes. El set de datos de dígitos es un ejemplo: cada píxel registra un número entre 0 y 255. Carguemos los datos:

library(tidyverse)
library(dslabs)
if(!exists("mnist")) mnist <- read_mnist()

En estos casos, a menudo es conveniente guardar los predictores en una matriz y el resultado en un vector en lugar de utilizar un data frame. Pueden ver que los predictores se guardan en una matriz:

class(mnist$train$images)
#> [1] "matrix" "array"

Esta matriz representa 60,000 dígitos, así que para los ejemplos en este capítulo, usaremos un subconjunto más manejable. Tomaremos los primeros 1,000 predictores x y etiquetas y:

x <- mnist$train$images[1:1000,]
y <- mnist$train$labels[1:1000]

La razón principal para usar matrices es que ciertas operaciones matemáticas necesarias para desarrollar código eficiente se pueden realizar usando técnicas de una rama de las matemáticas llamada álgebra lineal. De hecho, álgebra lineal y notación matricial son elementos claves del lenguaje utilizado en trabajos académicos que describen técnicas de machine learning. No cubriremos álgebra lineal en detalle aquí, pero demostraremos cómo usar matrices en R para que puedan aplicar las técnicas de álgebra lineal ya implementadas en la base R u otros paquetes.

Para motivar el uso de matrices, plantearemos cinco preguntas/desafíos:

1. ¿Algunos dígitos requieren más tinta que otros? Estudien la distribución de la oscuridad total de píxeles y cómo varía según los dígitos.

2. ¿Algunos píxeles no son informativos? Estudien la variación de cada píxel y eliminen los predictores (columnas) asociados con los píxeles que no cambian mucho y, por lo tanto, no proveen mucha información para la clasificación.

3. ¿Podemos eliminar las manchas? Primero, observen la distribución de todos los valores de píxeles. Usen esto para elegir un umbral para definir el espacio no escrito. Luego, cambien cualquier valor por debajo de ese umbral a 0.

4. Binaricen los datos. Primero, observen la distribución de todos los valores de píxeles. Usen esto para elegir un umbral para distinguir entre escritura y no escritura. Luego, conviertan todas las entradas en 1 o 0, respectivamente.

5. Escalen cada uno de los predictores en cada entrada para tener el mismo promedio y desviación estándar.

Para completar esto, tendremos que realizar operaciones matemáticas que involucran varias variables. El tidyverse no está desarrollado para realizar este tipo de operaciones matemáticas. Para esta tarea, es conveniente usar matrices.

Antes de hacer esto, presentaremos la notación matricial y el código R básico para definir y operar en matrices.

33.1.1 Notación

En álgebra matricial, tenemos tres tipos principales de objetos: escalares, vectores y matrices. Un escalar es solo un número, por ejemplo \(a = 1\). Para denotar escalares en notación matricial, generalmente usamos una letra minúscula no en negrilla.

Los vectores son como los vectores numéricos que definimos en R: incluyen varias entradas escalares. Por ejemplo, la columna que contiene el primer píxel:

length(x[,1])
#> [1] 1000

tiene 1,000 entradas. En álgebra matricial, utilizamos la siguiente notación para un vector que representa un atributo/predictor:

\[ \begin{pmatrix} x_1\\\ x_2\\\ \vdots\\\ x_N \end{pmatrix} \]

Del mismo modo, podemos usar la notación matemática para representar diferentes atributos matemáticamente agregando un índice:

\[ \mathbf{X}_1 = \begin{pmatrix} x_{1,1}\\ \vdots\\ x_{N,1} \end{pmatrix} \mbox{ and } \mathbf{X}_2 = \begin{pmatrix} x_{1,2}\\ \vdots\\ x_{N,2} \end{pmatrix} \]

Si estamos escribiendo una columna, como \(\mathbf{X}_1\), en una oración, a menudo usamos la notación: \(\mathbf{X}_1 = ( x_{1,1}, \dots x_{N,1})^\top\) con \(^\top\) la operación de transposición que convierte las columnas en filas y las filas en columnas.

Una matriz se puede definir como una serie de vectores del mismo tamaño unidos como columnas:

x_1 <- 1:5
x_2 <- 6:10
cbind(x_1, x_2)
#>      x_1 x_2
#> [1,]   1   6
#> [2,]   2   7
#> [3,]   3   8
#> [4,]   4   9
#> [5,]   5  10

Matemáticamente, los representamos con letras mayúsculas en negrilla:

\[ \mathbf{X} = [ \mathbf{X}_1 \mathbf{X}_2 ] = \begin{pmatrix} x_{1,1}&x_{1,2}\\ \vdots\\ x_{N,1}&x_{N,2} \end{pmatrix} \]

La dimensión de una matriz a menudo es un atributo importante necesario para asegurar que se puedan realizar ciertas operaciones. La dimensión es un resumen de dos números definido como el número de filas \(\times\) el número de columnas. En R, podemos extraer la dimensión de una matriz con la función dim:

dim(x)
#> [1] 1000  784

Los vectores pueden considerarse \(N\times 1\) matrices. Sin embargo, en R, un vector no tiene dimensiones:

dim(x_1)
#> NULL

No obstante, explícitamente convertimos un vector en una matriz usando la función as.matrix:

dim(as.matrix(x_1))
#> [1] 5 1

Podemos usar esta notación para denotar un número arbitrario de predictores con la siguiente matriz \(N\times p\), por ejemplo, con \(p=784\):

\[ \mathbf{X} = \begin{pmatrix} x_{1,1}&\dots & x_{1,p} \\ x_{2,1}&\dots & x_{2,p} \\ & \vdots & \\ x_{N,1}&\dots & x_{N,p} \end{pmatrix} \]

Almacenamos esta matriz en x:

dim(x)
#> [1] 1000  784

Ahora aprenderemos varias operaciones útiles relacionadas con el álgebra matricial. Utilizamos tres de las preguntas motivadoras mencionadas anteriormente.

33.1.2 Convertir un vector en una matriz

A menudo es útil convertir un vector en una matriz. Por ejemplo, debido a que las variables son píxeles en una cuadrícula, podemos convertir las filas de intensidades de píxeles en una matriz que representa esta cuadrícula.

Podemos convertir un vector en una matriz con la función matrix y especificando el número de filas y columnas que debe tener la matriz resultante. La matriz se llena por columna: la primera columna se llena primero, luego la segunda y así sucesivamente. Este ejemplo ayuda a ilustrar:

my_vector <- 1:15
mat <- matrix(my_vector, 5, 3)
mat
#>      [,1] [,2] [,3]
#> [1,]    1    6   11
#> [2,]    2    7   12
#> [3,]    3    8   13
#> [4,]    4    9   14
#> [5,]    5   10   15

Podemos llenar por fila usando el argumento byrow. Entonces, por ejemplo, para transponer la matriz mat, podemos usar:

mat_t <- matrix(my_vector, 3, 5, byrow = TRUE)
mat_t
#>      [,1] [,2] [,3] [,4] [,5]
#> [1,]    1    2    3    4    5
#> [2,]    6    7    8    9   10
#> [3,]   11   12   13   14   15

Cuando convertimos las columnas en filas, nos referimos a las operaciones como transponer la matriz. La función t se puede usar para transponer directamente una matriz:

identical(t(mat), mat_t)
#> [1] TRUE

Advertencia: La función matrix recicla valores en el vector sin advertencia si el producto de las columnas y las filas no coincide con la longitud del vector:

matrix(my_vector, 4, 5)
#> Warning in matrix(my_vector, 4, 5): la longitud de los datos [15] no es
#> un submúltiplo o múltiplo del número de filas [4] en la matriz
#>      [,1] [,2] [,3] [,4] [,5]
#> [1,]    1    5    9   13    2
#> [2,]    2    6   10   14    3
#> [3,]    3    7   11   15    4
#> [4,]    4    8   12    1    5

Para poner las intensidades de píxeles de nuestra, digamos, tercera entrada, que es 4 en la cuadrícula, podemos usar:

grid <- matrix(x[3,], 28, 28)

Para confirmar que lo hemos hecho correctamente, podemos usar la función image, que muestra una imagen de su tercer argumento. La parte superior de este gráfico es el píxel 1, que se muestra en la parte inferior para que la imagen se voltee. A continuación incluimos el código que muestra cómo voltearlo:

image(1:28, 1:28, grid)
image(1:28, 1:28, grid[, 28:1])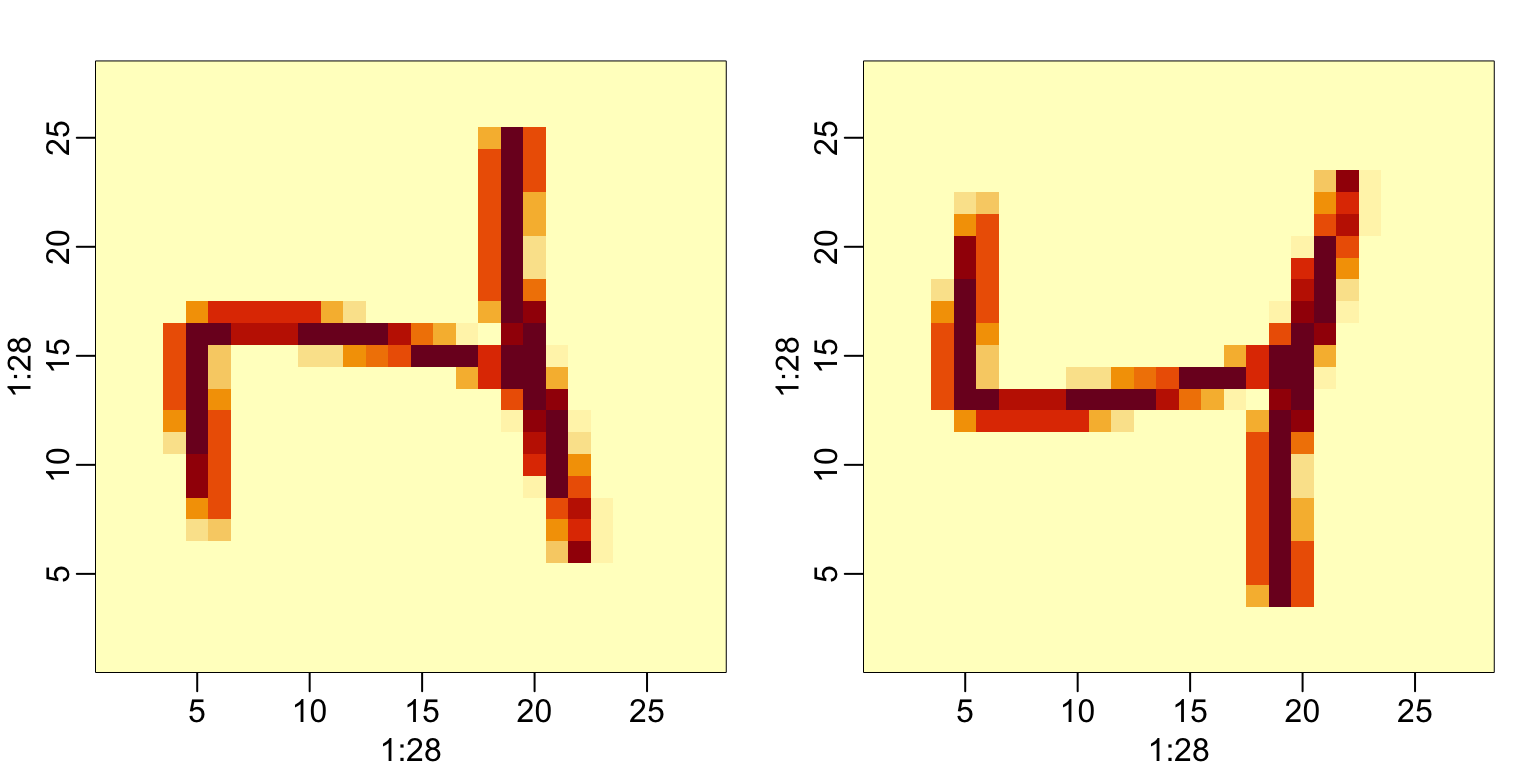

33.1.3 Resúmenes de filas y columnas

Para la primera tarea, relacionada con la oscuridad total de píxeles, queremos sumar los valores de cada fila y luego visualizar cómo estos valores varían por dígito.

La función rowSums toma una matriz como entrada y calcula los valores deseados:

sums <- rowSums(x)

También podemos calcular los promedios con rowMeans si queremos que los valores permanezcan entre 0 y 255:

avg <- rowMeans(x)

Una vez que tengamos esto, podemos generar un diagrama de caja:

tibble(labels = as.factor(y), row_averages = avg) |>
  qplot(labels, row_averages, data = _, geom = "boxplot")

De este gráfico vemos que, como era de esperar, los 1s usan menos tinta que los otros dígitos.

Podemos calcular las sumas y los promedios de la columna usando la función colSums y colMeans, respectivamente.

El paquete matrixStats agrega funciones que realizan operaciones en cada fila o columna de manera muy eficiente, incluyendo las funciones rowSds y colSds.

33.1.4 apply

Las funciones que acabamos de describir están realizando una operación similar a la que hacen sapply y la función map de purrr: aplicar la misma función a una parte de su objeto. En este caso, la función se aplica a cada fila o cada columna. La función apply les permite aplicar cualquier función, no solo sum o mean, a una matriz. El primer argumento es la matriz, el segundo es la dimensión (1 para las filas y 2 para las columnas) y el tercero es la función. Así, por ejemplo, rowMeans se puede escribir como:

avgs <- apply(x, 1, mean)

Pero noten que al igual que con sapply y map, podemos ejecutar cualquier función. Entonces, si quisiéramos la desviación estándar para cada columna, podríamos escribir:

sds <- apply(x, 2, sd)

La desventaja de esta flexibilidad es que estas operaciones no son tan rápidas como las funciones dedicadas, como rowMeans.

33.1.5 Filtrar columnas basado en resúmenes

Ahora pasamos a la tarea 2: estudiar la variación de cada píxel y eliminar las columnas asociadas con píxeles que no cambian mucho y, por lo tanto, no informan la clasificación. Aunque es un enfoque simplista, cuantificaremos la variación de cada píxel con su desviación estándar en todas las entradas. Como cada columna representa un píxel, utilizamos la función colSds del paquete matrixStats:

library(matrixStats)
sds <- colSds(x)

Un vistazo rápido a la distribución de estos valores muestra que algunos píxeles tienen una variabilidad muy baja de entrada a entrada:

qplot(sds, bins = "30", color = I("black"))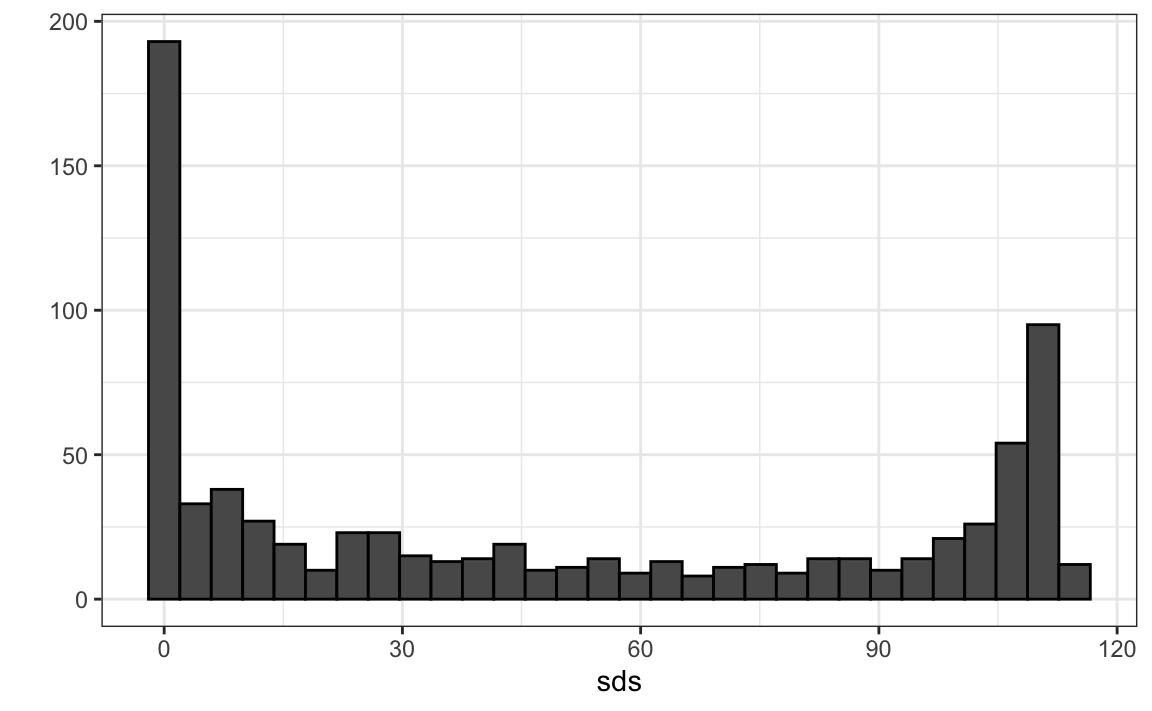

Esto tiene sentido ya que no escribimos en algunas partes del cuadro. Aquí está la variación graficada por ubicación:

image(1:28, 1:28, matrix(sds, 28, 28)[, 28:1])

Vemos que hay poca variación en las esquinas.

Podríamos eliminar atributos que no tienen variación ya que estos no nos ayuda a predecir. En la Sección 2.4.7, describimos las operaciones utilizadas para extraer columnas:

x[ ,c(351,352)]

y para extraer filas:

x[c(2,3),]

Además, podemos usar índices lógicos para determinar qué columnas o filas mantener. Entonces, si quisiéramos eliminar predictores no informativos de nuestra matriz, podríamos escribir esta línea de código:

new_x <- x[ ,colSds(x) > 60]
dim(new_x)
#> [1] 1000  314

Solo se mantienen las columnas para las que la desviación estándar es superior a 60, lo que elimina más de la mitad de los predictores.

Aquí agregamos una advertencia importante relacionada con el subconjunto de matrices: si seleccionan una columna o una fila, el resultado ya no es una matriz sino un vector.

class(x[,1])
#> [1] "integer"
dim(x[1,])
#> NULL

Sin embargo, podemos preservar la clase de matriz usando el argumento drop=FALSE:

class(x[ , 1, drop=FALSE])
#> [1] "matrix" "array"
dim(x[, 1, drop=FALSE])
#> [1] 1000    1

33.1.6 Indexación con matrices

Podemos hacer rápidamente un histograma de todos los valores en nuestro set de datos. Vimos cómo podemos convertir vectores en matrices. También podemos deshacer esto y convertir matrices en vectores. La operación se realiza por fila:

mat <- matrix(1:15, 5, 3)
as.vector(mat)
#>  [1]  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15

Para ver un histograma de todos nuestros datos predictores, podemos usar:

qplot(as.vector(x), bins = 30, color = I("black"))

Notamos una clara dicotomía que se explica como partes de la imagen con tinta y partes sin ella. Si creemos que los valores menor que, digamos, 50 son manchas, podemos cambiarlos a cero usando:

new_x <- x
new_x[new_x < 50] <- 0

Para ver un ejemplo de cómo esto ocurre, usamos una matriz más pequeña:

mat <- matrix(1:15, 5, 3)
mat[mat < 3] <- 0
mat
#>      [,1] [,2] [,3]
#> [1,]    0    6   11
#> [2,]    0    7   12
#> [3,]    3    8   13
#> [4,]    4    9   14
#> [5,]    5   10   15

También podemos usar operadores lógicas con una matriz de valores logicos:

mat <- matrix(1:15, 5, 3)
mat[mat > 6 & mat < 12] <- 0
mat
#>      [,1] [,2] [,3]
#> [1,]    1    6    0
#> [2,]    2    0   12
#> [3,]    3    0   13
#> [4,]    4    0   14
#> [5,]    5    0   15

33.1.7 Binarizar los datos

El histograma anterior parece sugerir que estos datos son principalmente binarios. Un píxel tiene tinta o no. Usando lo que hemos aprendido, podemos binarizar los datos usando solo operaciones de matrices:

bin_x <- x
bin_x[bin_x < 255/2] <- 0
bin_x[bin_x > 255/2] <- 1

También podemos convertir a una matriz de valores lógicos y luego forzar una conversión a números como este:

bin_X <- (x > 255/2)*1

33.1.8 Vectorización para matrices

En R, si restamos un vector de una matriz, el primer elemento del vector se resta de la primera fila, el segundo elemento de la segunda fila, y así sucesivamente. Usando notación matemática, lo escribiríamos de la siguiente manera:

\[ \begin{pmatrix} X_{1,1}&\dots & X_{1,p} \\ X_{2,1}&\dots & X_{2,p} \\ & \vdots & \\ X_{N,1}&\dots & X_{N,p} \end{pmatrix} - \begin{pmatrix} a_1\\\ a_2\\\ \vdots\\\ a_N \end{pmatrix} = \begin{pmatrix} X_{1,1}-a_1&\dots & X_{1,p} -a_1\\ X_{2,1}-a_2&\dots & X_{2,p} -a_2\\ & \vdots & \\ X_{N,1}-a_n&\dots & X_{N,p} -a_n \end{pmatrix} \]

Lo mismo es válido para otras operaciones aritméticas. Esto implica que podemos escalar cada fila de una matriz así:

(x - rowMeans(x))/ rowSds(x)

Si desean escalar cada columna, tengan cuidado ya que este enfoque no funciona para las columnas. Para realizar una operación similar, convertimos las columnas en filas usando la transposición t, procedemos como se indica arriba y volvemos a transponer:

t(t(X) - colMeans(X))

También podemos usar la función sweep que funciona de manera similar a apply. Toma cada entrada de un vector y la resta de la fila o columna correspondiente.

X_mean_0 <- sweep(x, 2, colMeans(x))

La función sweep tiene otro argumento que les permite definir la operación aritmética. Entonces, para dividir por la desviación estándar, hacemos lo siguiente:

x_mean_0 <- sweep(x, 2, colMeans(x))
x_standardized <- sweep(x_mean_0, 2, colSds(x), FUN = "/")

33.1.9 Operaciones de álgebra matricial

Finalmente, aunque no discutimos las operaciones de álgebra matricial, como la multiplicación de matrices, compartimos aquí los comandos relevantes para aquellos que conocen las matemáticas y quieren aprender el código:

1. La multiplicación de matrices se realiza con %*%. Por ejemplo, el producto cruzado es:

t(x) %*% x

2. Podemos calcular el producto cruzado directamente con la función:

crossprod(x)

3. Para calcular el inverso de una función, usamos solve. Aquí se aplica al producto cruzado:

solve(crossprod(x))

4. La descomposición QR está fácilmente disponible mediante el uso de la función qr:

qr(x)

33.2 Ejercicios

1. Cree una matriz de 100 por 10 de números normales generados aleatoriamente. Ponga el resultado en x.

2. Aplique las tres funciones de R que le dan la dimensión de x, el número de filas de x y el número de columnas de x, respectivamente.

3. Agregue el escalar 1 a la fila 1, el escalar 2 a la fila 2 y así sucesivamente, a la matriz x.

4. Agregue el escalar 1 a la columna 1, el escalar 2 a la columna 2 y así sucesivamente, a la matriz x. Sugerencia: use sweep con FUN = "+".

5. Calcule el promedio de cada fila de x.

6. Calcule el promedio de cada columna de x.

7. Para cada dígito en los datos de entrenamiento MNIST, calcule la proporción de píxeles que se encuentran en un área gris, definida como valores entre 50 y 205. Haga un diagrama de caja basado en clase de dígitos. Sugerencia: utilice operadores lógicos y rowMeans.

33.3 Distancia

Muchos de los análisis que realizamos con datos de alta dimensión se relacionan directa o indirectamente con la distancia. La mayoría de las técnicas de agrupamiento y machine learning se basan en la capacidad de definir la distancia entre observaciones, utilizando atributos (features en inglés) o predictores.

33.3.1 Distancia euclidiana

Como repaso, definamos la distancia entre dos puntos, \(A\) y \(B\), en un plano cartesiano.

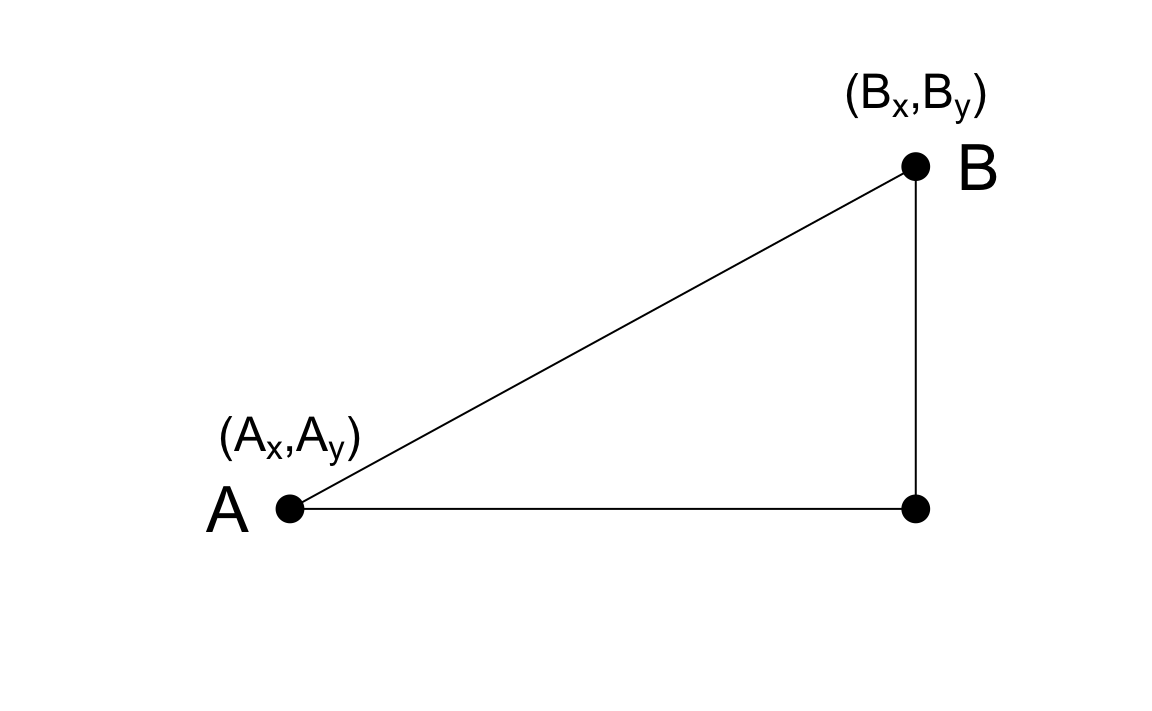
La distancia euclidiana entre \(A\) y \(B\) es simplemente:

\[ \mbox{dist}(A,B) = \sqrt{ (A_x-B_x)^2 + (A_y-B_y)^2} \]

Esta definición se aplica al caso de una dimensión, en la que la distancia entre dos números es el valor absoluto de su diferencia. Entonces, si nuestros dos números unidimensionales son \(A\) y \(B\), la distancia es:

\[ \mbox{dist}(A,B) = \sqrt{ (A - B)^2 } = | A - B | \]

33.3.2 Distancia en dimensiones superiores

Anteriormente presentamos un set de datos de entrenamiento con matriz para 784 atributos. Con fines ilustrativos, veremos una muestra aleatoria de 2s y 7s.

library(tidyverse)
library(dslabs)

if(!exists("mnist")) mnist <- read_mnist()

set.seed(1995)
ind <- which(mnist$train$labels %in% c(2,7)) |> sample(500)
x <- mnist$train$images[ind,]
y <- mnist$train$labels[ind]

Los predictores están en x y las etiquetas en y.

Para el propósito de, por ejemplo, suavizamiento, estamos interesados en describir la distancia entre observaciones; en este caso, dígitos. Más adelante, con el fin de seleccionar atributos, también podríamos estar interesados en encontrar píxeles que se comporten de manera similar en todas las muestras.

Para definir la distancia, necesitamos saber qué son puntos, ya que la distancia matemática se calcula entre puntos. Con datos de alta dimensión, los puntos ya no están en el plano cartesiano. En cambio, los puntos están en dimensiones más altas. Ya no podemos visualizarlos y necesitamos pensar de manera abstracta. Por ejemplo, predictores \(\mathbf{X}_i\) se definen como un punto en el espacio dimensional 784: \(\mathbf{X}_i = (x_{i,1},\dots,x_{i,784})^\top\).

Una vez que definamos los puntos de esta manera, la distancia euclidiana se define de manera muy similar a la de dos dimensiones. Por ejemplo, la distancia entre los predictores para dos observaciones, digamos observaciones \(i=1\) y \(i=2\), es:

\[ \mbox{dist}(1,2) = \sqrt{ \sum_{j=1}^{784} (x_{1,j}-x_{2,j })^2 } \]

Este es solo un número no negativo, tal como lo es para dos dimensiones.

33.3.3 Ejemplo de distancia euclidiana

Las etiquetas para las tres primeras observaciones son:

y[1:3]
#> [1] 7 2 7

Los vectores de predictores para cada una de estas observaciones son:

x_1 <- x[1,]
x_2 <- x[2,]
x_3 <- x[3,]

El primer y tercer número son 7s y el segundo es un 2. Esperamos que las distancias entre el mismo número:

sqrt(sum((x_1 - x_2)^2))
#> [1] 3273

sean más pequeñas que entre diferentes números:

sqrt(sum((x_1 - x_3)^2))
#> [1] 2311
sqrt(sum((x_2 - x_3)^2))
#> [1] 2636

Como se esperaba, los 7s están más cerca uno del otro.

Una forma más rápida de calcular esto es usar álgebra matricial:

sqrt(crossprod(x_1 - x_2))
#>      [,1]
#> [1,] 3273
sqrt(crossprod(x_1 - x_3))
#>      [,1]
#> [1,] 2311
sqrt(crossprod(x_2 - x_3))
#>      [,1]
#> [1,] 2636

También podemos calcular todas las distancias a la vez de manera relativamente rápida utilizando la función dist, que calcula la distancia entre cada fila y produce un objeto de clase dist:

d <- dist(x)
class(d)
#> [1] "dist"

Hay varias funciones relacionadas con machine learning en R que toman objetos de clase dist como entrada. Para acceder a las entradas usando índices de fila y columna, necesitamos forzar d a ser una matriz. Podemos ver la distancia que calculamos arriba de esta manera:

as.matrix(d)[1:3,1:3]
#>      1    2    3
#> 1    0 3273 2311
#> 2 3273    0 2636
#> 3 2311 2636    0

Rápidamente vemos una imagen de estas distancias usando este código:

image(as.matrix(d))

Si ordenamos esta distancia por las etiquetas, podemos ver que, en general, los 2s están más cerca uno del otro y los 7s están más cerca el uno del otro:

image(as.matrix(d)[order(y), order(y)])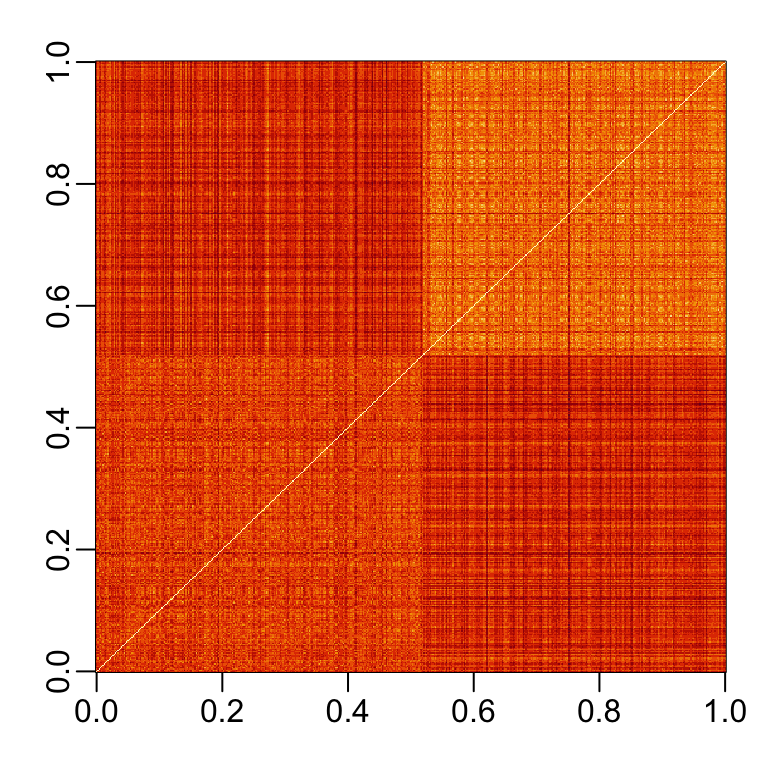

Algo que notamos aquí es que parece haber más uniformidad en la forma en que se dibujan los 7s, ya que parecen estar más cercas (más rojos) a otros 7s que los 2s a otros 2s.

33.3.4 Espacio predictor

El espacio predictor (predictor space en inglés) es un concepto que a menudo se usa para describir algoritmos de machine learning. El término espacio se refiere a una definición matemática que no describimos en detalle aquí. En cambio, ofrecemos una explicación simplificada para ayudar a entender el término espacio predictor cuando se usa en el contexto de algoritmos de machine learning.

El espacio predictor puede considerarse como la colección de todos los posibles vectores de predictores que deben considerarse para el reto en cuestión de machine learning. Cada miembro del espacio se conoce como un punto. Por ejemplo, en el set de datos 2 o 7, el espacio predictor consta de todos los pares \((x_1, x_2)\) tal que ambos \(x_1\) y \(x_2\) están dentro de 0 y 1. Este espacio en particular puede representarse gráficamente como un cuadrado. En el set de datos MNIST, el espacio predictor consta de todos los vectores de 784 dimensiones, con cada elemento vectorial un número entero entre 0 y 256. Un elemento esencial de un espacio predictor es que necesitamos definir una función que nos de la distancia entre dos puntos. En la mayoría de los casos, usamos la distancia euclidiana, pero hay otras posibilidades. Un caso particular en el que no podemos simplemente usar la distancia euclidiana es cuando tenemos predictores categóricos.

Definir un espacio predictor es útil en machine learning porque hacemos cosas como definir vecindarios de puntos, como lo requieren muchas técnicas de suavización. Por ejemplo, podemos definir un vecindario como todos los puntos que están dentro de 2 unidades de un centro predefinido. Si los puntos son bidimensionales y usamos la distancia euclidiana, este vecindario se representa gráficamente como un círculo con radio 2. En tres dimensiones, el vecindario es una esfera. Pronto aprenderemos sobre algoritmos que dividen el espacio en regiones que no se superponen y luego hacen diferentes predicciones para cada región utilizando los datos de la región.

33.3.5 Distancia entre predictores

También podemos calcular distancias entre predictores. Si \(N\) es el número de observaciones, la distancia entre dos predictores, digamos 1 y 2, es:

\[ \mbox{dist}(1,2) = \sqrt{ \sum_{i=1}^{N} (x_{i,1}-x_{i,2})^2 } \]

Para calcular la distancia entre todos los pares de los 784 predictores, primero podemos transponer la matriz y luego usar dist:

d <- dist(t(x))
dim(as.matrix(d))
#> [1] 784 784

33.4 Ejercicios

1. Cargue el siguiente set de datos:

data("tissue_gene_expression")

Este set de datos incluye una matriz x:

dim(tissue_gene_expression$x)

con la expresión génica medida en 500 genes para 189 muestras biológicas que representan siete tejidos diferentes. El tipo de tejido se almacena en y:

table(tissue_gene_expression$y)

Calcule la distancia entre cada observación y almacénela en un objeto d.

2. Compare la distancia entre las dos primeras observaciones (ambos cerebelos), las observaciones 39 y 40 (ambos colones) y las observaciones 73 y 74 (ambos endometrios). Vea si las observaciones del mismo tipo de tejido están más cercanas entre sí.

3. Vemos que, de hecho, las observaciones del mismo tipo de tejido están más cercanas entre sí en los seis ejemplos de tejido que acabamos de examinar. Haga un diagrama de todas las distancias usando la función image para ver si este patrón es general. Sugerencia: primero convierta d en una matriz.

33.5 Reducción de dimensiones

Un reto típico de machine learning incluirá una gran cantidad de predictores, lo que hace que la visualización sea algo retante. Hemos mostrado métodos para visualizar datos univariados y emparejados, pero los gráficos que revelan relaciones entre muchas variables son más complicados en dimensiones más altas. Por ejemplo, para comparar cada uno de las 784 atributos en nuestro ejemplo de predicción de dígitos, tendríamos que crear, por ejemplo, 306,936 diagramas de dispersión. La creación de un único diagrama de dispersión de los datos es imposible debido a la alta dimensionalidad.

Aquí describimos técnicas eficaces y útiles para el análisis exploratorio de datos, entre otras cosas, generalmente conocidas como reducción de dimensiones. La idea general es reducir la dimensión del set de datos mientras se conservan características importantes, como la distancia entre atributos u observaciones. Con menos dimensiones, la visualización es más factible. La técnica detrás de todo, la descomposición de valores singulares, también es útil en otros contextos. El análisis de componentes principales (principal component analysis o PCA por sus siglas en inglés) es el enfoque que mostraremos. Antes de aplicar PCA a sets de datos de alta dimensión, motivaremos las ideas con un ejemplo sencillo.

33.5.1 Preservando la distancia

Consideremos un ejemplo con alturas de gemelos. Algunas parejas son adultas, otras son niños. Aquí simulamos 100 puntos bidimensionales que representan el número de desviaciones estándar que cada individuo tiene respecto a la altura media. Cada punto es un par de gemelos. Utilizamos la función mvrnorm del paquete MASS para simular datos de distribución normal de dos variables.

set.seed(1988)
library(MASS)
n <- 100
Sigma <- matrix(c(9, 9 * 0.9, 9 * 0.92, 9 * 1), 2, 2)
x <- rbind(mvrnorm(n/ 2, c(69, 69), Sigma),
           mvrnorm(n/ 2, c(55, 55), Sigma))

Un diagrama de dispersión revela que la correlación es alta y que hay dos grupos de gemelos, los adultos (puntos superiores derechos) y los niños (puntos inferiores izquierdos):

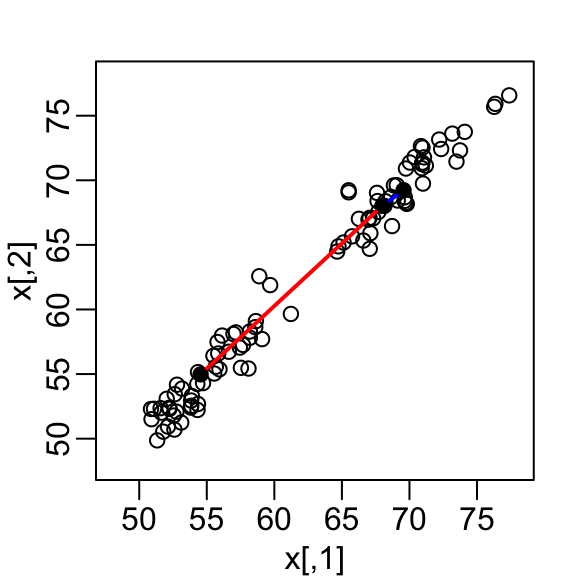
Nuestros atributos son \(N\) puntos bidimensionales, las dos alturas y, con fines ilustrativos, finjiremos como si visualizar dos dimensiones es demasiado difícil. Por lo tanto, queremos reducir las dimensiones de dos a una, pero todavía poder entender atributos importantes de los datos, por ejemplo, que las observaciones se agrupan en dos grupos: adultos y niños.

Consideremos un desafío específico: queremos un resumen unidimensional de nuestros predictores a partir del cual podamos aproximar la distancia entre dos observaciones. En el gráfico anterior, mostramos la distancia entre la observación 1 y 2 (azul) y la observación 1 y 51 (rojo). Noten que la línea azul es más corta, que implica que 1 y 2 están más cerca.

Podemos calcular estas distancias usando dist:

d <- dist(x)
as.matrix(d)[1, 2]
#> [1] 1.98
as.matrix(d)[2, 51]
#> [1] 18.7

Esta distancia se basa en dos dimensiones y necesitamos una aproximación de distancia basada en solo una.

Comencemos con un enfoque simplista de solo eliminar una de las dos dimensiones. Comparemos las distancias reales con la distancia calculada solo con la primera dimensión:

z <- x[,1]

Aquí están las distancias aproximadas versus las distancias originales:

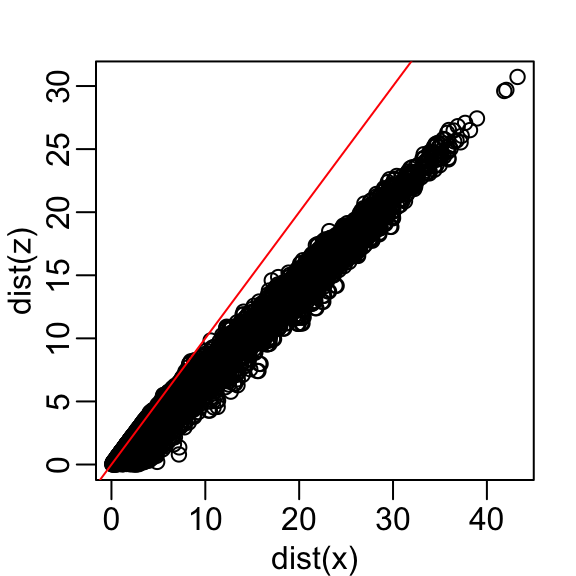
El gráfico se ve casi igual si usamos la segunda dimensión. Obtenemos una subestimación general. Esto no sorprende porque estamos añadiendo más cantidades positivas al cálculo de la distancia a medida que aumentamos el número de dimensiones. Si, en cambio, usamos un promedio, como este:

\[\sqrt{ \frac{1}{2} \sum_{j=1}^2 (X_{1,j}-X_{2,j})^2 },\]

entonces la subestimación desaparece. Dividimos la distancia por \(\sqrt{2}\) para lograr la corrección.

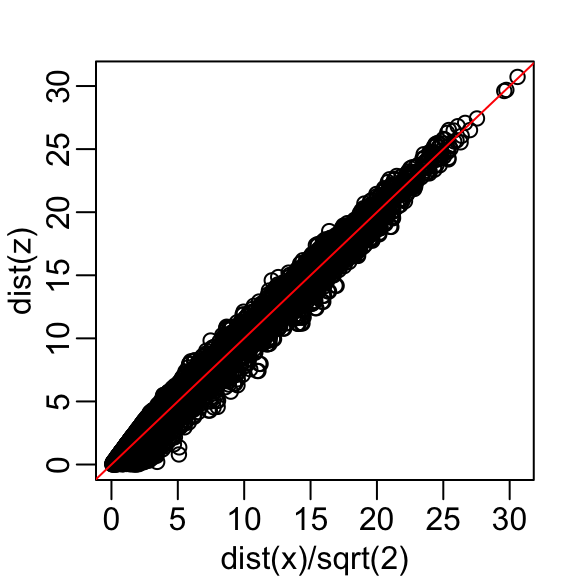
Esto funciona bastante bien y obtenemos una diferencia típica de:

sd(dist(x) - dist(z)*sqrt(2))
#> [1] 1.21

Ahora, ¿podemos elegir un resumen unidimensional que haga que esta aproximación sea aún mejor?

Si consideramos el diagrama de dispersión anterior y visualizamos una línea entre cualquier par de puntos, la longitud de esta línea es la distancia entre los dos puntos. Estas líneas tienden a ir a lo largo de la dirección de la diagonal. Noten que si en su lugar graficamos la diferencia versus el promedio:

z <- cbind((x[,2] + x[,1])/2, x[,2] - x[,1])

podemos ver cómo la distancia entre puntos se explica principalmente por la primera dimensión: el promedio.

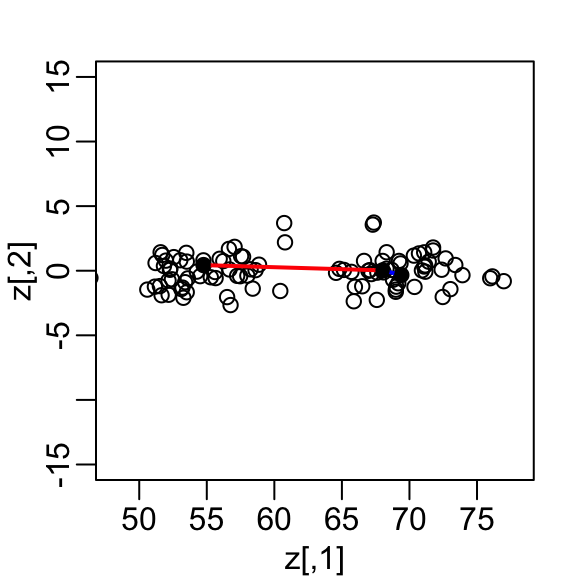
Esto significa que podemos ignorar la segunda dimensión y no perder demasiada información. Si la línea es completamente plana, no perdemos ninguna información. Usando la primera dimensión de esta matriz transformada, obtenemos una aproximación aún mejor:

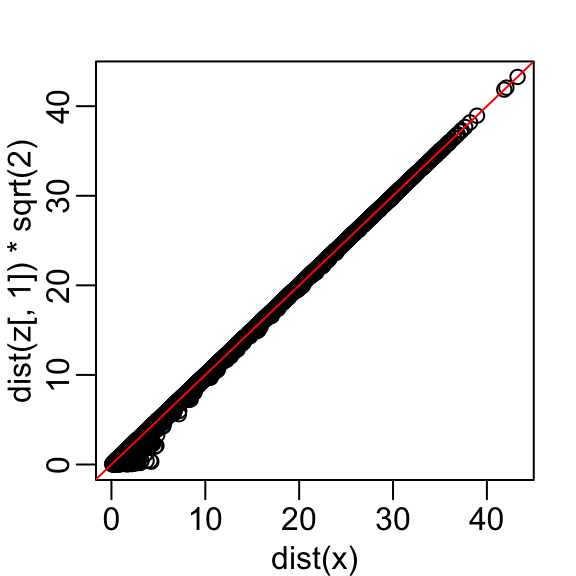
con la diferencia típica mejorada aproximadamente un 35%:

sd(dist(x) - dist(z[,1])*sqrt(2))
#> [1] 0.315

Más tarde, aprendemos que z[,1] es el primer componente principal de la matriz x.

33.5.2 Transformaciones lineales (avanzado)

Tengan en cuenta que cada fila de \(X\) se transformó usando una transformación lineal. Para cualquier fila \(i\), la primera entrada fue:

\[Z_{i,1} = a_{1,1} X_{i,1} + a_{2,1} X_{i,2}\]

con \(a_{1,1} = 0.5\) y \(a_{2,1} = 0.5\).

La segunda entrada también fue una transformación lineal:

\[Z_{i,2} = a_{1,2} X_{i,1} + a_{2,2} X_{i,2}\]

con \(a_{1,2} = 1\) y \(a_{2,2} = -1\).

Además, podemos usar la transformación lineal para obtener \(X\) de \(Z\):

\[X_{i,1} = b_{1,1} Z_{i,1} + b_{2,1} Z_{i,2}\]

con \(b_{1,2} = 1\) y \(b_{2,1} = 0.5\) y

\[X_{i,2} = b_{2,1} Z_{i,1} + b_{2,2} Z_{i,2}\]

con \(b_{2,1} = 1\) y \(a_{1,2} = -0.5\).

Si saben álgebra lineal, pueden escribir la operación que acabamos de realizar de esta manera:

\[ Z = X A \mbox{ with } A = \, \begin{pmatrix} 1/2&1\\ 1/2&-1\\ \end{pmatrix}. \]

Y que podemos transformar de vuelta a \(X\) multiplicando por \(A^{-1}\) así:

\[ X = Z A^{-1} \mbox{ with } A^{-1} = \, \begin{pmatrix} 1&1\\ 1/2&-1/2\\ \end{pmatrix}. \]

La reducción de dimensiones frecuentemente se puede describir como la aplicación de una transformación \(A\) a una matriz \(X\) con muchas columnas que mueven la información contenida en \(X\) a las primeras columnas de \(Z=AX\), manteniendo solo estas pocas columnas informativas y reduciendo así la dimensión de los vectores contenidos en las filas.

33.5.3 Transformaciones ortogonales (avanzado)

Noten que dividimos lo anterior por \(\sqrt{2}\) para tomar en cuenta las diferencias en las dimensiones al comparar una distancia de 2 dimensiones con una distancia de 1 dimensión. De hecho, podemos garantizar que las escalas de distancia sigan siendo las mismas si volvemos a escalar las columnas de \(A\) para asegurar que la suma de cuadrados es 1:

\[a_{1,1}^2 + a_{2,1}^2 = 1\mbox{ and } a_{1,2}^2 + a_{2,2}^2=1,\]

y que la correlación de las columnas es 0:

\[ a_{1,1} a_{1,2} + a_{2,1} a_{2,2} = 0. \]

Recuerden que si las columnas están centradas para tener un promedio de 0, entonces la suma de los cuadrados es equivalente a la varianza o desviación estándar al cuadrado.

En nuestro ejemplo, para lograr ortogonalidad, multiplicamos el primer set de coeficientes (primera columna de \(A\)) por \(\sqrt{2}\) y el segundo por \(1/\sqrt{2}\). Entonces obtenemos la misma distancia exacta cuando usamos ambas dimensiones:

z[,1] <- (x[,1] + x[,2])/ sqrt(2)
z[,2] <- (x[,2] - x[,1])/ sqrt(2)

Esto nos da una transformación que preserva la distancia entre dos puntos:

max(dist(z) - dist(x))
#> [1] 3.24e-14

y una aproximación mejorada si usamos solo la primera dimensión:

sd(dist(x) - dist(z[,1]))
#> [1] 0.315

En este caso, \(Z\) se llama una rotación ortogonal de \(X\): conserva las distancias entre filas.

Tengan en cuenta que al usar la transformación anterior, podemos resumir la distancia entre cualquier par de gemelos con una sola dimensión. Por ejemplo, una exploración de datos unidimensionales de la primera dimensión de \(Z\) muestra claramente que hay dos grupos, adultos y niños:

library(tidyverse)
qplot(z[,1], bins = 20, color = I("black"))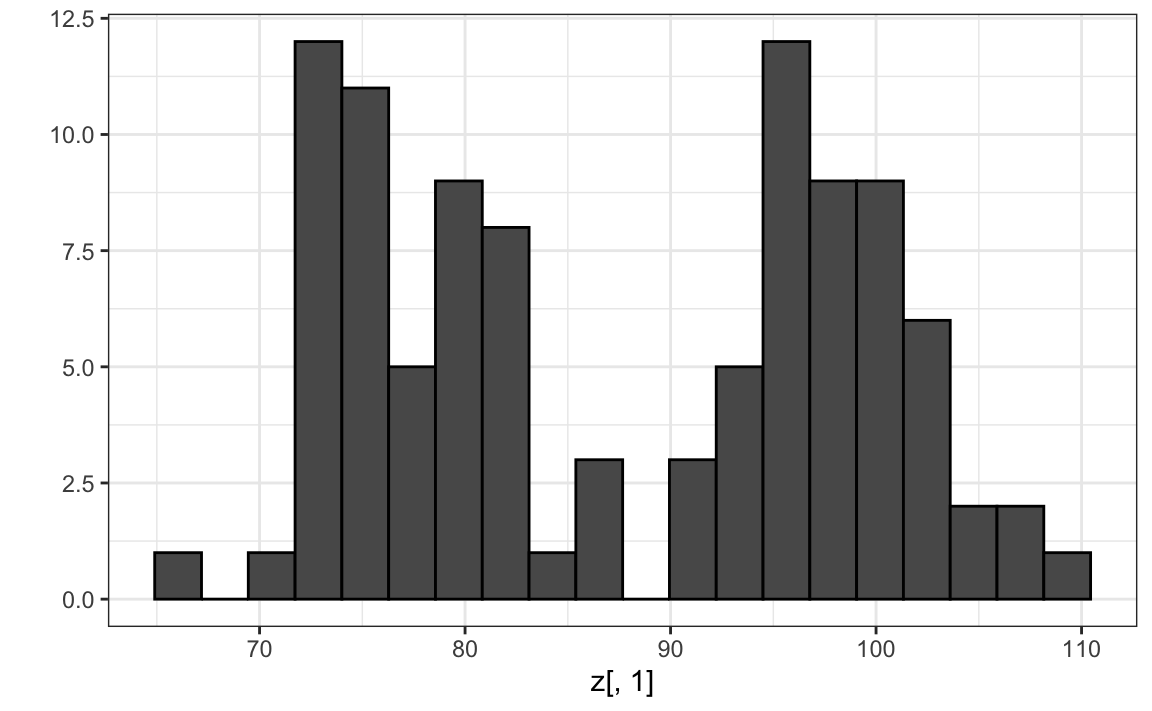

Redujimos exitosamente el número de dimensiones de dos a uno con muy poca pérdida de información.

La razón por la que pudimos hacer esto es porque las columnas de \(X\) estaban muy correlacionadas:

cor(x[,1], x[,2])
#> [1] 0.988

y la transformación produjo columnas no correlacionadas con información “independiente” en cada columna:

cor(z[,1], z[,2])
#> [1] 0.0876

Una forma en que esta información puede ser útil en una aplicación de machine learning es que podemos reducir la complejidad de un modelo utilizando solo \(Z_1\) en lugar de ambos \(X_1\) y \(X_2\).

Es común obtener datos con varios predictores altamente correlacionados. En estos casos, PCA, que describimos a continuación, puede ser bastante útil para reducir la complejidad del modelo que se está ajustando.

33.5.4 Análisis de componentes principales

En el cálculo anterior, la variabilidad total en nuestros datos puede definirse como la suma de la suma de los cuadrados de las columnas. Suponemos que las columnas están centradas, por lo que esta suma es equivalente a la suma de las varianzas de cada columna:

\[ v_1 + v_2, \mbox{ with } v_1 = \frac{1}{N}\sum_{i=1}^N X_{i,1}^2 \mbox{ and } v_2 = \frac{1}{N}\sum_{i=1}^N X_{i,2}^2 \]

Podemos calcular \(v_1\) y \(v_2\) al utilizar:

colMeans(x^2)
#> [1] 3904 3902

y podemos mostrar matemáticamente que si aplicamos una transformación ortogonal como la anterior, la variación total sigue siendo la misma:

sum(colMeans(x^2))
#> [1] 7806
sum(colMeans(z^2))
#> [1] 7806

Sin embargo, mientras que la variabilidad en las dos columnas de X es casi la misma, en la versión transformada \(Z\), el 99% de la variabilidad se incluye solo en la primera dimensión:

v <- colMeans(z^2)
v/sum(v)
#> [1] 1.00e+00 9.93e-05

El primer componente principal (principal component o PC por sus siglas en inglés) de una matriz \(X\) es la transformación ortogonal lineal de \(X\) que maximiza esta variabilidad. La función prcomp provee esta información:

pca <- prcomp(x)
pca$rotation
#>         PC1    PC2
#> [1,] -0.702  0.712
#> [2,] -0.712 -0.702

Tengan en cuenta que el primer PC es casi el mismo que ese proporcionado por el \((X_1 + X_2)/ \sqrt{2}\) que utilizamos anteriormente (excepto quizás por un cambio de signo que es arbitrario).

La función prcomp devuelve la rotación necesaria para transformar \(X\) para que la variabilidad de las columnas disminuya de más variable a menos (se accede con $rotation) así como la nueva matriz resultante (que se accede con $x). Por defecto, prcomp centra las columnas de \(X\) antes de calcular las matrices.

Entonces, usando la multiplicación de matrices que se muestra arriba, notamos que las dos siguientes operaciones dan el mismo resultado (demostrado por una diferencia entre elementos de prácticamente cero):

a <- sweep(x, 2, colMeans(x))
b <- pca$x %*% t(pca$rotation)
max(abs(a - b))
#> [1] 3.55e-15

La rotación es ortogonal, lo que significa que el inverso es su transposición. Entonces también tenemos que estos dos son idénticos:

a <- sweep(x, 2, colMeans(x)) %*% pca$rotation
b <- pca$x
max(abs(a - b))
#> [1] 0

Podemos visualizarlos para ver cómo el primer componente resume los datos. En el gráfico a continuación, el rojo representa valores altos y el azul representa valores negativos. Más adelante, en la Sección 33.11.1, aprendemos por qué llamamos a estos pesos (weights en inglés) y patrones (patterns en inglés):

Resulta que podemos encontrar esta transformación lineal no solo para dos dimensiones, sino también para matrices de cualquier dimensión \(p\).

Para una matriz multidimensional \(X\) con \(p\) columnas, se puede encontrar una transformación \(Z\) que conserva la distancia entre filas, pero con la varianza de las columnas en orden decreciente. La segunda columna es el segundo componente principal, la tercera columna es el tercer componente principal y así sucesivamente. Como en nuestro ejemplo, si después de un cierto número de columnas, digamos \(k\), las variaciones de las columnas de \(Z_j\) con \(j>k\) son muy pequeñas, significa que estas dimensiones tienen poco que contribuir a la distancia y podemos aproximar la distancia entre dos puntos con solo \(k\) dimensiones. Si \(k\) es mucho más pequeño que \(p\), entonces podemos lograr un resumen muy eficiente de nuestros datos.

33.5.5 Ejemplo de lirios

Los datos del lirio (iris en inglés) son un ejemplo ampliamente utilizado en los cursos de análisis de datos. Incluye cuatro medidas botánicas relacionadas con tres especies de flores:

names(iris)
#> [1] "Sepal.Length" "Sepal.Width"  "Petal.Length" "Petal.Width" 
#> [5] "Species"

Si imprimen iris$Species, verán que los datos están ordenados por especie.

Calculemos la distancia entre cada observación. Pueden ver claramente las tres especies con una especie muy diferente de las otras dos:

x <- iris[,1:4] |> as.matrix()
d <- dist(x)
image(as.matrix(d), col = rev(RColorBrewer::brewer.pal(9, "RdBu")))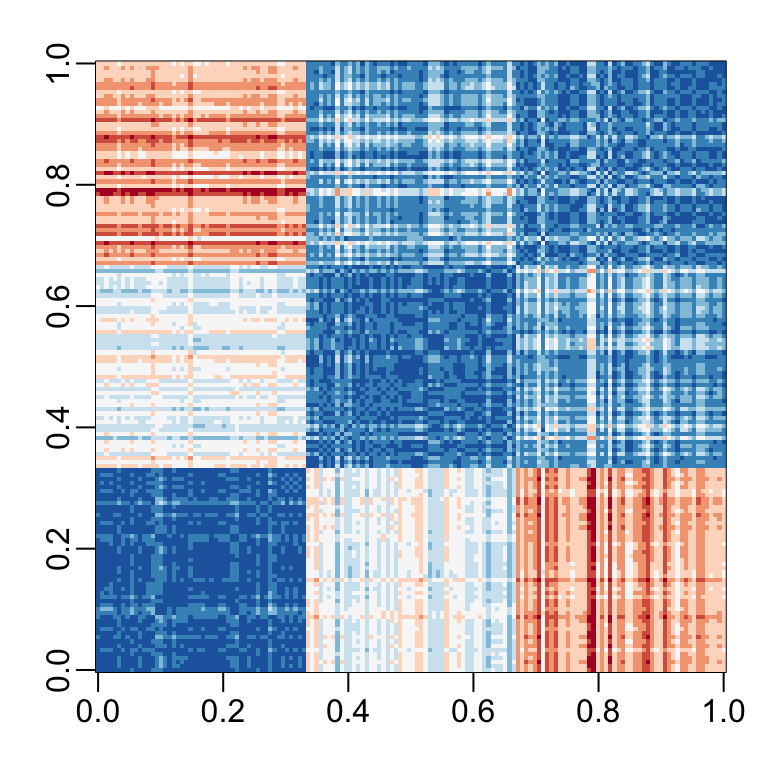

Nuestros predictores aquí tienen cuatro dimensiones, pero tres están muy correlacionadas:

cor(x)
#>              Sepal.Length Sepal.Width Petal.Length Petal.Width
#> Sepal.Length        1.000      -0.118        0.872       0.818
#> Sepal.Width        -0.118       1.000       -0.428      -0.366
#> Petal.Length        0.872      -0.428        1.000       0.963
#> Petal.Width         0.818      -0.366        0.963       1.000

Si aplicamos PCA, deberíamos poder aproximar esta distancia con solo dos dimensiones, comprimiendo las dimensiones altamente correlacionadas. Utilizando la función summary, podemos ver la variabilidad explicada por cada PC:

pca <- prcomp(x)
summary(pca)
#> Importance of components:
#>                          PC1    PC2    PC3     PC4
#> Standard deviation     2.056 0.4926 0.2797 0.15439
#> Proportion of Variance 0.925 0.0531 0.0171 0.00521
#> Cumulative Proportion  0.925 0.9777 0.9948 1.00000

Las dos primeras dimensiones representan el 97% de la variabilidad. Por lo tanto, deberíamos poder aproximar bien la distancia con dos dimensiones. Podemos visualizar los resultados de PCA:

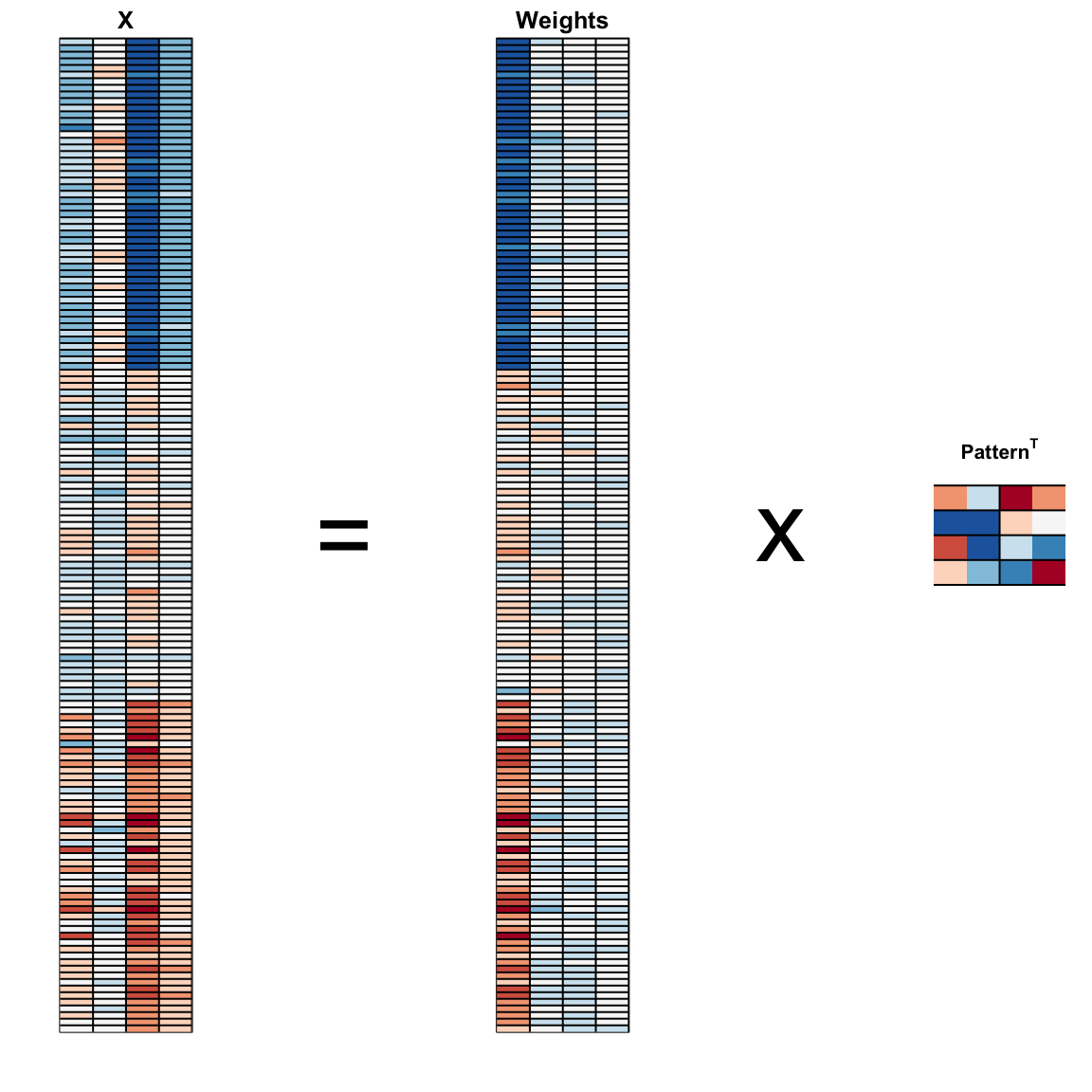
Y ver que el primer patrón es la longitud del sépalo, la longitud del pétalo y el ancho del pétalo (rojo) en una dirección y el ancho del sépalo (azul) en la otra. El segundo patrón es la longitud del sépalo y el ancho del pétalo en una dirección (azul) y la longitud y el ancho del pétalo en la otra (rojo). Pueden ver de los pesos que la primera PC1 controla la mayor parte de la variabilidad y separa claramente el primer tercio de las muestras (setosa) de los dos tercios (versicolor y virginica). Si miran la segunda columna de los pesos, observarán que separa un poco versicolor (rojo) de virginica (azul).

Podemos ver esto mejor al graficar los dos primeros PCs con color representando especie:

data.frame(pca$x[,1:2], Species=iris$Species) |>
  ggplot(aes(PC1,PC2, fill = Species))+
  geom_point(cex=3, pch=21) +
  coord_fixed(ratio = 1)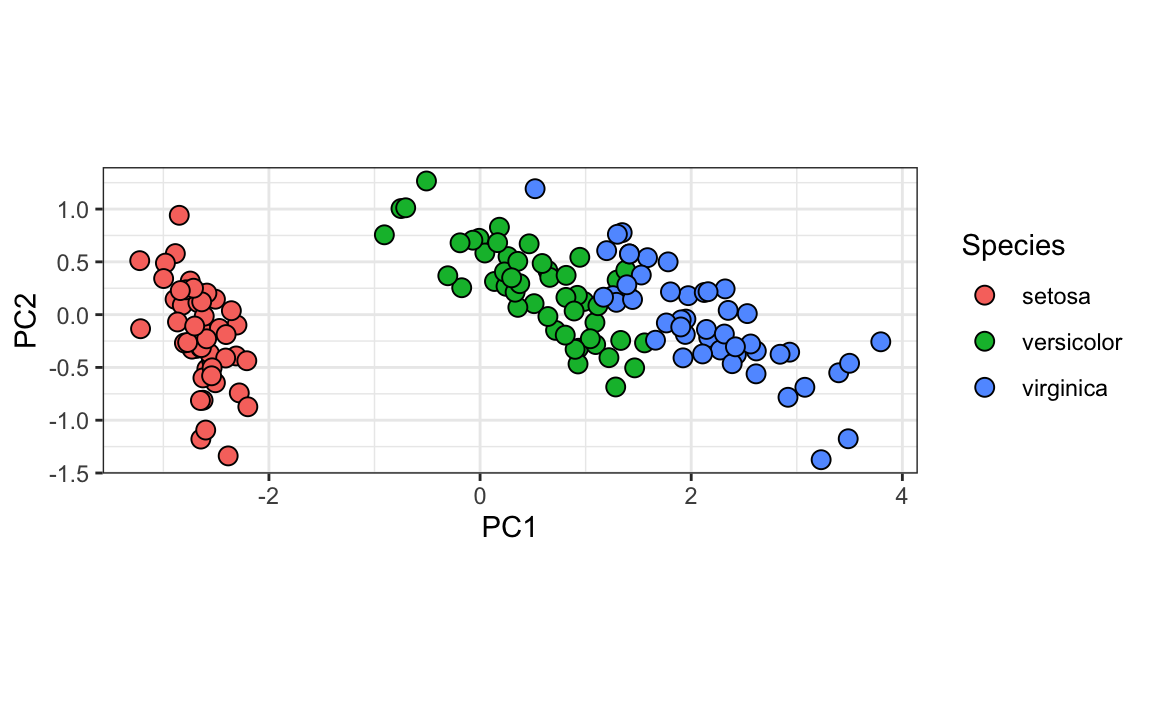

Vemos que las dos primeras dimensiones preservan la distancia:

d_approx <- dist(pca$x[, 1:2])
qplot(d, d_approx) + geom_abline(color="red")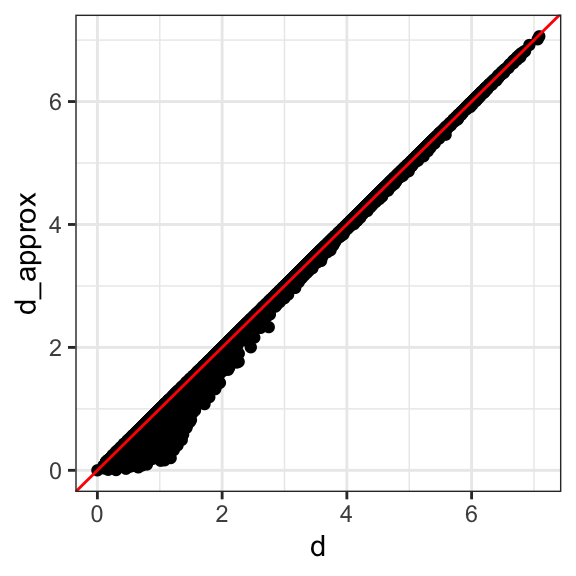

Este ejemplo es más realista que el primer ejemplo artificial que utilizamos, ya que mostramos cómo podemos visualizar los datos usando dos dimensiones cuando los datos eran de cuatro dimensiones.

33.5.6 Ejemplo de MNIST

El ejemplo de dígitos escritos tiene 784 atributos. ¿Hay espacio para la reducción de datos? ¿Podemos crear algoritmos sencillos de machine learning con menos atributos?

Carguemos los datos:

library(dslabs)
if(!exists("mnist")) mnist <- read_mnist()

Debido a que los píxeles son tan pequeños, esperamos que los píxeles cercanos entre sí en la cuadrícula estén correlacionados, lo que significa que la reducción de dimensión debería ser posible.

Probemos PCA y exploremos la variación de los PCs. Esto tomará unos segundos ya que es una matriz bastante grande.

col_means <- colMeans(mnist$test$images)
pca <- prcomp(mnist$train$images)

pc <- 1:ncol(mnist$test$images)
qplot(pc, pca$sdev)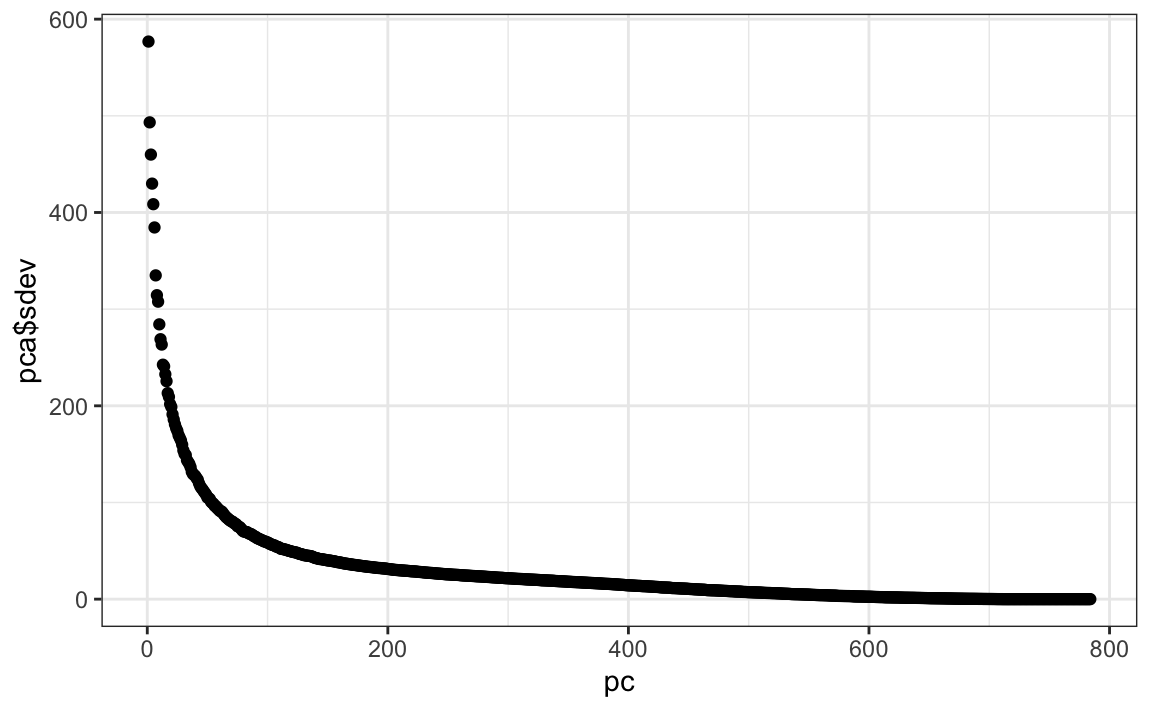

Podemos ver que los primeros PCs ya explican un gran porcentaje de la variabilidad:

summary(pca)$importance[,1:5]
#>                            PC1     PC2      PC3      PC4      PC5
#> Standard deviation     576.823 493.238 459.8993 429.8562 408.5668
#> Proportion of Variance   0.097   0.071   0.0617   0.0539   0.0487
#> Cumulative Proportion    0.097   0.168   0.2297   0.2836   0.3323

Y con solo mirar las dos primeras PCs vemos información sobre la clase. Aquí hay una muestra aleatoria de 2,000 dígitos:

data.frame(PC1 = pca$x[,1], PC2 = pca$x[,2],
           label=factor(mnist$train$label)) |>
  sample_n(2000) |>
  ggplot(aes(PC1, PC2, fill=label))+
  geom_point(cex=3, pch=21)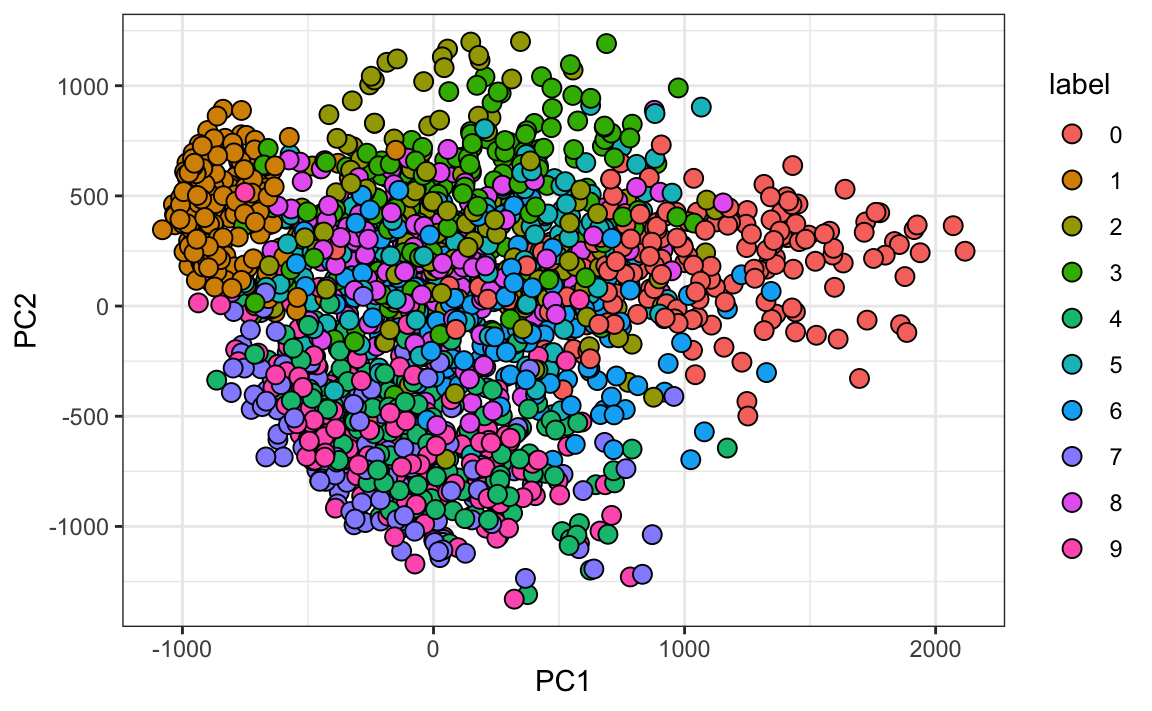

También podemos ver las combinaciones lineales en la cuadrícula para tener una idea de lo que se está ponderando:

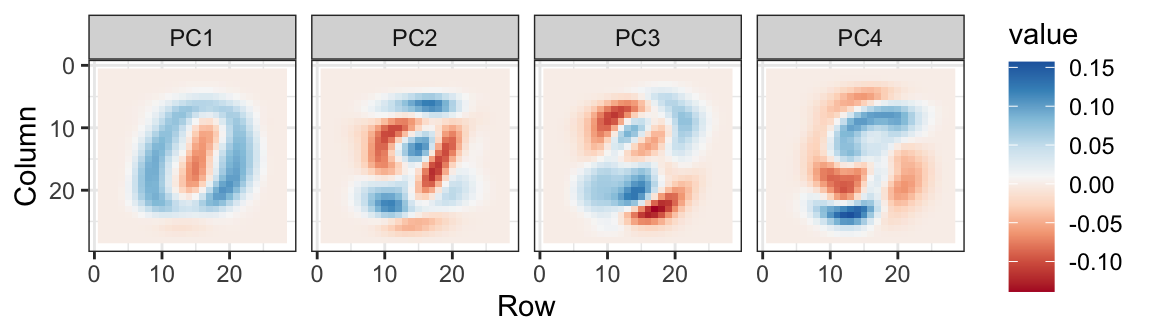
Los PCs de menor varianza parecen estar relacionadas a la variabilidad irrelevante en las esquinas:

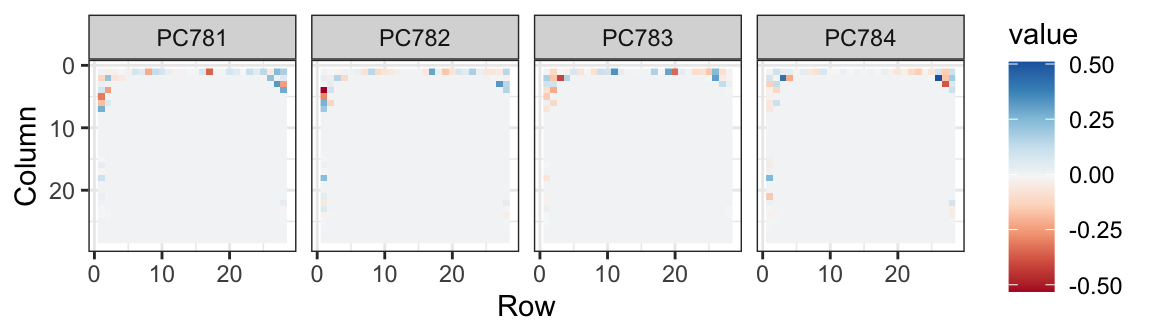
Ahora apliquemos la transformación que aprendimos con los datos de entrenamiento a los datos de evaluación, reduzcamos la dimensión y ejecutemos knn3 en solo un pequeño número de dimensiones.

Intentamos 36 dimensiones ya que esto explica aproximadamente el 80% de los datos. Primero, ajuste el modelo:

library(caret)
k <- 36
x_train <- pca$x[,1:k]
y <- factor(mnist$train$labels)
fit <- knn3(x_train, y)

Ahora, transformen el set de evaluación:

x_test <- sweep(mnist$test$images, 2, col_means) %*% pca$rotation
x_test <- x_test[,1:k]

Y estamos listos para predecir y evaluar los resultados:

y_hat <- predict(fit, x_test, type = "class")
confusionMatrix(y_hat, factor(mnist$test$labels))$overall["Accuracy"]
#> Accuracy 
#>    0.975

Con solo 36 dimensiones, obtenemos una exactitud muy superior a 0.95.

33.6 Ejercicios

1. Queremos explorar los predictores tissue_gene_expression graficándolos.

data("tissue_gene_expression")
dim(tissue_gene_expression$x)

Procuramos tener una idea de qué observaciones están cercas entre sí, pero como los predictores son de 500 dimensiones, es difícil graficar. Grafique los dos primeros componentes principales con color representando el tipo de tejido.

2. Los predictores de cada observación se miden en el mismo dispositivo de medición (un microarreglo de expresión génica) después de un procedimiento experimental. Se utiliza un dispositivo y procedimiento diferente para cada observación. Esto puede introducir sesgos que afecten a todos los predictores de cada observación de la misma manera. Para explorar el efecto de este posible sesgo, para cada observación, calcule el promedio de todos los predictores y luego grafique esto contra el primer PC con el color que representa el tejido. Indique la correlación.

3. Vemos una asociación con el primer PC y los promedios de observación. Vuelva a hacer el PCA pero solo después de quitar el centro.

4. Para los primeros 10 PCs, haga un diagrama de caja que muestre los valores para cada tejido.

5. Grafique el porcentaje de varianza explicado por el número de PC. Sugerencia: use la función summary.

33.7 Sistemas de recomendación

Los sistemas de recomendación utilizan clasificaciones que los consumidores le han dado a artículos para hacer recomendaciones específicas. Las compañías que venden muchos productos a muchos clientes y permiten que estos clientes califiquen sus productos, como Amazon, pueden recopilar sets de datos masivos que se pueden utilizar para predecir qué calificación le otorgará un usuario en particular a un artículo específico. Artículos para los cuales se predice una calificación alta para un usuario particular, se recomiendan a ese usuario.

Netflix utiliza un sistema de recomendación para predecir cuántas estrellas le dará un usuario a una película específica. Una estrella sugiere que no es una buena película, mientras que cinco estrellas sugieren que es una película excelente. Aquí, ofrecemos los conceptos básicos de cómo se hacen estas recomendaciones, motivados por algunos de los enfoques adoptados por los ganadores del Netflix challenge.

En octubre de 2006, Netflix le dio un reto a la comunidad de ciencia de datos: mejoren nuestro algoritmo de recomendación por un 10% y ganen un millón de dólares. En septiembre de 2009, los ganadores se anunciaron¹²⁰. Pueden leer un buen resumen de cómo se creó el algoritmo ganador aquí: http://blog.echen.me/2011/10/24/winning-the-netflix-prize-a-summary/ y una explicación más detallada aquí: http://www.netflixprize.com/assets/GrandPrize2009_BPC_BellKor.pdf. Ahora le mostraremos algunas de las estrategias de análisis de datos utilizadas por el equipo ganador.

33.7.1 Datos de Movielens

Los datos de Netflix no están disponibles públicamente, pero el laboratorio de investigación GroupLens¹²¹ generó su propia base de datos con más de 20 millones de calificaciones para más de 27,000 películas por más de 138,000 usuarios. Ponemos a disposición un pequeño subconjunto de estos datos a través del paquete dslabs:

library(tidyverse)
library(dslabs)
data("movielens")

Podemos ver que esta tabla está en formato tidy con miles de filas:

movielens |> as_tibble()
#> # A tibble: 100,004 × 7
#>   movieId title                      year genres userId rating timestamp
#>     <int> <chr>                     <int> <fct>   <int>  <dbl>     <int>
#> 1      31 Dangerous Minds            1995 Drama       1    2.5    1.26e9
#> 2    1029 Dumbo                      1941 Anima…      1    3      1.26e9
#> 3    1061 Sleepers                   1996 Thril…      1    3      1.26e9
#> 4    1129 Escape from New York       1981 Actio…      1    2      1.26e9
#> 5    1172 Cinema Paradiso (Nuovo c…  1989 Drama       1    4      1.26e9
#> # … with 99,999 more rows

Cada fila representa una calificación dada por un usuario a una película.

Podemos ver la cantidad de usuarios únicos que dan calificaciones y cuántas películas únicas fueron calificadas:

movielens |>
  summarize(n_users = n_distinct(userId),
            n_movies = n_distinct(movieId))
#>   n_users n_movies
#> 1     671     9066

Si multiplicamos esos dos números, obtenemos un número mayor de 5 millones. Sin embargo, nuestra tabla de datos tiene aproximadamente 100,000 filas. Esto implica que no todos los usuarios calificaron todas las películas. Por lo tanto, podemos pensar en estos datos como una matriz muy grande, con usuarios en las filas y películas en las columnas, con muchas celdas vacías. La función pivot_longer nos permite convertirla a este formato, pero si lo intentamos para toda la matriz, colgaremos a R. Mostremos la matriz para seis usuarios y cuatro películas.

userId	Pulp Fiction	Shawshank Redemption	Forrest Gump	Silence of the Lambs
13	3.5	4.5	5.0	NA
15	5.0	2.0	1.0	5.0
16	NA	4.0	NA	NA
17	5.0	5.0	2.5	4.5
19	5.0	4.0	5.0	3.0
20	0.5	4.5	2.0	0.5

Pueden pensar en la tarea de un sistema de recomendación como completar los NAs en la tabla de arriba. Para ver cuán dispersa es la matriz, aquí tenemos la matriz para una muestra aleatoria de 100 películas y 100 usuarios con amarillo indicando una combinación de usuario/película para la que tenemos una calificación.

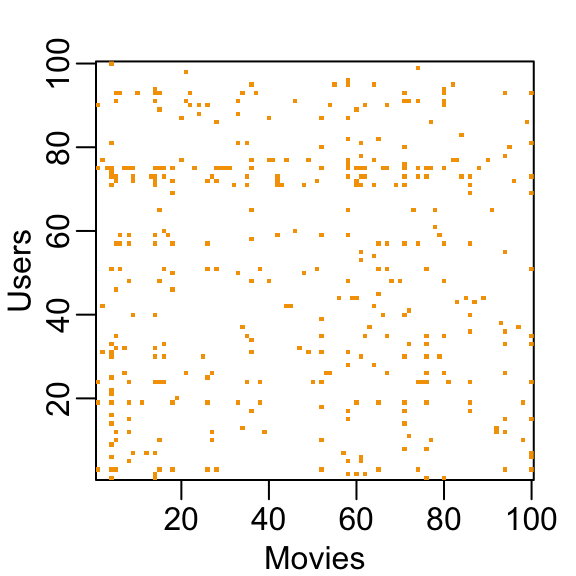
Este reto de machine learning es más complicado de lo que hemos estudiado hasta ahora porque cada resultado \(Y\) tiene un set diferente de predictores. Para ver esto, tengan en cuenta que si estamos prediciendo la calificación de la película \(i\) por usuario \(u\), en principio, todas las otras clasificaciones relacionadas con la película \(i\) y por el usuario \(u\) pueden usarse como predictores, pero diferentes usuarios califican diferentes películas y diferentes números de películas. Además, podemos usar información de otras películas que hemos determinado que son parecidas a la película \(i\) o de usuarios que se consideran similares al usuario \(u\). Básicamente, toda la matriz se puede utilizar como predictores para cada celda.

Veamos algunas de las propiedades generales de los datos para entender mejor los retos.

Lo primero que notamos es que algunas películas se evalúan más que otras. A continuación se muestra la distribución. Esto no debería sorprendernos dado que hay películas de gran éxito vistas por millones y películas artísticas e independientes vistas por pocos. Nuestra segunda observación es que algunos usuarios son más activos que otros en la calificación de películas:

33.7.2 Sistemas de recomendación como un desafío de machine learning

Para ver cómo esto se puede considerar machine learning, noten que necesitamos construir un algoritmo con los datos que hemos recopilado que luego se aplicarán fuera de nuestro control, a medida que los usuarios busquen recomendaciones de películas. Así que creamos un set de evaluación para evaluar la exactitud de los modelos que implementamos.

library(caret)
set.seed(755)
test_index <- createDataPartition(y = movielens$rating, times = 1, p = 0.2,
                                  list = FALSE)
train_set <- movielens[-test_index,]
test_set <- movielens[test_index,]

Para asegurarnos de que no incluimos usuarios y películas en el set de evaluación que no aparecen en el set de entrenamiento, eliminamos estas entradas usando la función semi_join:

test_set <- test_set |>
  semi_join(train_set, by = "movieId") |>
  semi_join(train_set, by = "userId")

33.7.3 Función de pérdida

El Netflix challenge usó la pérdida de error típica: decidieron un ganador basado en la desviación cuadrática media (RMSE por sus siglas en inglés) en un set de evaluación. Definimos \(y_{u,i}\) como la calificación de la película \(i\) por usuario \(u\) y denotamos nuestra predicción con \(\hat{y}_{u,i}\). El RMSE se define entonces como:

\[ \mbox{RMSE} = \sqrt{\frac{1}{N} \sum_{u,i}^{} \left( \hat{y}_{u,i} - y_{u,i} \right)^2 } \] con \(N\) siendo el número de combinaciones de usuario/película y la suma que ocurre en todas estas combinaciones.

Recuerden que podemos interpretar el RMSE de manera similar a una desviación estándar: es el error típico que cometemos al predecir una calificación de película. Si este número es mayor que 1, significa que nuestro error típico es mayor que una estrella, lo cual no es bueno.

Escribamos una función que calcule el RMSE para vectores de clasificaciones y sus predictores correspondientes:

RMSE <- function(true_ratings, predicted_ratings){
  sqrt(mean((true_ratings - predicted_ratings)^2))
}

33.7.4 Un primer modelo

Comencemos construyendo el sistema de recomendación más sencillo posible: predecimos la misma calificación para todas las películas, independientemente del usuario. ¿Qué número debería ser esta predicción? Podemos usar un enfoque basado en modelos para responder a esto. Un modelo que supone la misma calificación para todas las películas y usuarios con todas las diferencias explicadas por la variación aleatoria se vería así:

\[ Y_{u,i} = \mu + \varepsilon_{u,i} \]

con \(\varepsilon_{i,u}\) errores independientes muestreados de la misma distribución centrada en 0 y \(\mu\) la calificación “verdadera” para todas las películas. Sabemos que el estimador que minimiza el RMSE es el estimador de mínimos cuadrados de \(\mu\) y, en este caso, es el promedio de todas las calificaciones:

mu_hat <- mean(train_set$rating)
mu_hat
#> [1] 3.54

Si predecimos todas las calificaciones desconocidas con \(\hat{\mu}\), obtenemos el siguiente RMSE:

naive_rmse <- RMSE(test_set$rating, mu_hat)
naive_rmse
#> [1] 1.05

Tengan en cuenta que si usan cualquier otro número, obtendrám un RMSE más alto. Por ejemplo:

predictions <- rep(3, nrow(test_set))
RMSE(test_set$rating, predictions)
#> [1] 1.19

Al observar la distribución de calificaciones, podemos visualizar que esta es la desviación estándar de esa distribución. Obtenemos un RMSE de aproximadamente 1. Para ganar el gran premio de $1,000,000, un equipo participante tuvo que obtener un RMSE de aproximadamente 0.857. ¡Definitivamente podemos mejorar!

A medida que avanzamos, compararemos diferentes enfoques. Comencemos creando una tabla de resultados con este enfoque simplista:

rmse_results <- tibble(method = "Just the average", RMSE = naive_rmse)

33.7.5 Modelando los efectos de películas

Sabemos por experiencia que algunas películas generalmente tienen una calificación más alta que otras. Esta intuición, que las diferentes películas se clasifican de manera diferente, la confirma los datos. Podemos expandir nuestro modelo anterior agregando el término \(b_i\) para representar la clasificación promedio de la película \(i\):

\[ Y_{u,i} = \mu + b_i + \varepsilon_{u,i} \]

Los libros de texto de estadísticas se refieren a \(b\)s como efectos. Sin embargo, en los artículos sobre el Netflix challenge, se refieren a ellos como “sesgo” (o bias en inglés; por lo tanto, la notación \(b\)).

De nuevo podemos usar mínimos cuadrados para estimar \(b_i\) de la siguiente manera:

fit <- lm(rating ~ as.factor(movieId), data = movielens)

Como hay miles de \(b_i\), a medida que cada película obtiene una, la función lm() será muy lenta aquí. Por eso, no recomendamos ejecutar el código anterior. Pero en esta situación particular, sabemos que el estimador de los mínimos cuadrados \(\hat{b}_i\) es solo el promedio de \(Y_{u,i} - \hat{\mu}\) para cada película \(i\). Entonces podemos calcularlos de esta manera (dejaremos de usar la notación hat en el código para representar los estimadores en el futuro):

mu <- mean(train_set$rating)
movie_avgs <- train_set |>
  group_by(movieId) |>
  summarize(b_i = mean(rating - mu))

Podemos ver que estos estimadores varían sustancialmente:

qplot(b_i, data = movie_avgs, bins = 10, color = I("black"))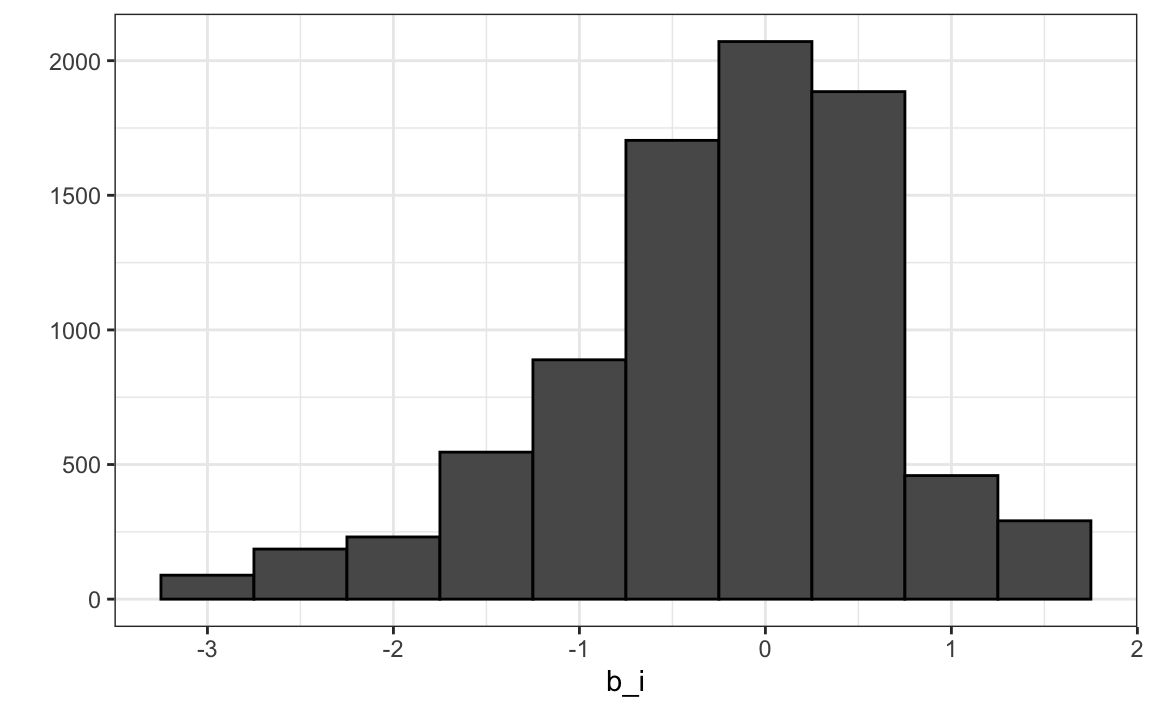

Recuerden \(\hat{\mu}=3.5\), entonces una \(b_i = 1.5\) implica una calificación perfecta de cinco estrellas.

Veamos cuánto mejora nuestra predicción cuando usamos \(\hat{y}_{u,i} = \hat{\mu} + \hat{b}_i\):

predicted_ratings <- mu + test_set |>
  left_join(movie_avgs, by='movieId') |>
  pull(b_i)
RMSE(predicted_ratings, test_set$rating)
#> [1] 0.989

Ya observamos una mejora. ¿Pero podemos mejorar más?

33.7.6 Efectos de usuario

Calculemos la calificación promedio para el usuario \(u\) para aquellos que han calificado 100 o más películas:

train_set |>
  group_by(userId) |>
  filter(n()>=100) |>
  summarize(b_u = mean(rating)) |>
  ggplot(aes(b_u)) +
  geom_histogram(bins = 30, color = "black")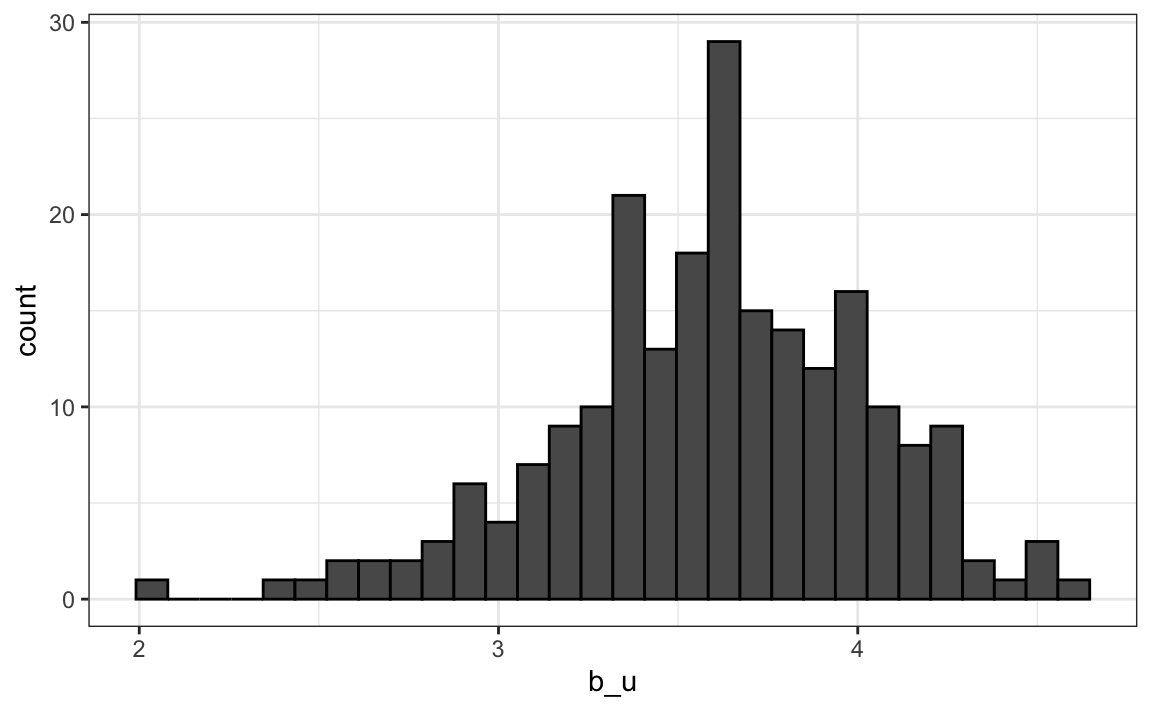

Noten que también existe una variabilidad sustancial entre los usuarios: algunos usuarios son muy exigentes y otros adoran cada película. Esto implica que una mejora adicional de nuestro modelo puede ser:

\[ Y_{u,i} = \mu + b_i + b_u + \varepsilon_{u,i} \]

dónde \(b_u\) es un efecto específico de cada usuario. Ahora, si un usuario exigente (\(b_u\) negativo) califica una película excelente (\(b_i\) positiva), los efectos se contrarrestan y podemos predecir correctamente que este usuario le dio a esta gran película un 3 en lugar de un 5.

Para ajustar este modelo, podríamos nuevamente usar lm así:

lm(rating ~ as.factor(movieId) + as.factor(userId))

pero, por las razones descritas anteriormente, no lo haremos. En cambio, calcularemos una aproximación calculando \(\hat{\mu}\) y \(\hat{b}_i\) y estimando \(\hat{b}_u\) como el promedio de \(y_{u,i} - \hat{\mu} - \hat{b}_i\):

user_avgs <- train_set |>
  left_join(movie_avgs, by='movieId') |>
  group_by(userId) |>
  summarize(b_u = mean(rating - mu - b_i))

Ahora podemos construir predictores y ver cuánto mejora el RMSE:

predicted_ratings <- test_set |>
  left_join(movie_avgs, by='movieId') |>
  left_join(user_avgs, by='userId') |>
  mutate(pred = mu + b_i + b_u) |>
  pull(pred)
RMSE(predicted_ratings, test_set$rating)
#> [1] 0.905

33.8 Ejercicios

1. Cargue los datos movielens.

data("movielens")

Calcule el número de calificaciones para cada película y luego compárelo con el año en que salió la película. Transforme los datos usando la raíz cuadrada en los recuentos.

2. Vemos que, en promedio, las películas que salieron después de 1993 obtienen más calificaciones. También vemos que con las películas más nuevas, a partir de 1993, el número de calificaciones disminuye con el año: entre más reciente sea una película, menos tiempo han tenido los usuarios para calificarla.

Entre las películas que salieron en 1993 o más tarde, ¿cuáles son las 25 películas con más calificaciones por año? Además, indique la calificación promedio.

3. De la tabla construida en el ejemplo anterior, vemos que las películas mejor calificadas tienden a tener calificaciones superiores al promedio. Esto no es sorprendente: más personas ven películas populares. Para confirmar esto, estratifique las películas posteriores a 1993 por calificaciones por año y calcule sus calificaciones promedio. Haga un gráfico de la calificación promedio versus calificaciones por año y muestre un estimador de la tendencia.

4. En el ejercicio anterior, vemos que entre más se califica una película, mayor es la calificación. Suponga que está haciendo un análisis predictivo en el que necesita completar las calificaciones faltantes con algún valor. ¿Cuál de las siguientes estrategias usaría?

1. Completar los valores faltantes con la calificación promedio de todas las películas.
2. Completar los valores faltantes con 0.
3. Completar el valor con un valor más bajo que el promedio ya que la falta de calificación se asocia con calificaciones más bajas. Pruebe diferentes valores y evalúe la predicción en un set de evaluación.
4. Ninguna de las anteriores.

5. El set de datos movielens también incluye un sello de tiempo. Esta variable representa el tiempo y los datos en los que se le dio la calificación. Las unidades son segundos desde el 1 de enero de 1970. Cree una nueva columna date con la fecha. Sugerencia: use la función as_datetime en el paquete lubridate.

6. Calcule la calificación promedio de cada semana y calcule este promedio para cada día. Sugerencia: use la función round_date antes de group_by.

7. El gráfico muestra alguna evidencia de un efecto temporero. Si definimos \(d_{u,i}\) como el día que el usuario \(u\) hizo su calificación de la película \(i\), ¿cuál de los siguientes modelos es el más apropiado?

1. \(Y_{u,i} = \mu + b_i + b_u + d_{u,i} + \varepsilon_{u,i}\).
2. \(Y_{u,i} = \mu + b_i + b_u + d_{u,i}\beta + \varepsilon_{u,i}\).
3. \(Y_{u,i} = \mu + b_i + b_u + d_{u,i}\beta_i + \varepsilon_{u,i}\).
4. \(Y_{u,i} = \mu + b_i + b_u + f(d_{u,i}) + \varepsilon_{u,i}\), con \(f\) una función suave de \(d_{u,i}\).

8. Los datos movielens también tienen un columna genres. Esta columna incluye todos los géneros que aplican a la película. Algunas películas pertenecen a varios géneros. Defina una categoría como cualquier combinación que aparezca en esta columna. Mantenga solo categorías con más de 1,000 calificaciones. Luego, calcule el promedio y error estándar para cada categoría. Grafique estos usando diagramas de barras de error.

9. El gráfico muestra evidencia convincente de un efecto de género. Si definimos \(g_{u,i}\) como el género para la calificación del usuario \(u\) de la película \(i\), ¿cuál de los siguientes modelos es el más apropiado?

1. \(Y_{u,i} = \mu + b_i + b_u + d_{u,i} + \varepsilon_{u,i}\).
2. \(Y_{u,i} = \mu + b_i + b_u + d_{u,i}\beta + \varepsilon_{u,i}\).
3. \(Y_{u,i} = \mu + b_i + b_u + \sum_{k=1}^K x_{u,i} \beta_k + \varepsilon_{u,i}\), con \(x^k_{u,i} = 1\) si \(g_{u,i}\) es genero \(k\).
4. \(Y_{u,i} = \mu + b_i + b_u + f(d_{u,i}) + \varepsilon_{u,i}\), con \(f\) una función suave de \(d_{u,i}\).

33.9 Regularización

33.9.1 Motivación

A pesar de la gran variación de película a película, nuestra mejora en RMSE fue solo como 5%. Exploremos dónde cometimos errores en nuestro primer modelo, usando solo efectos de película \(b_i\). Aquí están los 10 errores más grandes:

test_set |>
  left_join(movie_avgs, by='movieId') |>
  mutate(residual = rating - (mu + b_i)) |>
  arrange(desc(abs(residual))) |>
  slice(1:10) |>
  pull(title)
#>  [1] "Kingdom, The (Riget)"            "Heaven Knows, Mr. Allison"      
#>  [3] "American Pimp"                   "Chinatown"                      
#>  [5] "American Beauty"                 "Apocalypse Now"                 
#>  [7] "Taxi Driver"                     "Wallace & Gromit: A Close Shave"
#>  [9] "Down in the Delta"               "Stalag 17"

Todas estas parecen ser películas desconocidas. Para muchas de ellas, predecimos calificaciones altas. Echemos un vistazo a las 10 peores y 10 mejores películas basadas en \(\hat{b}_i\). Primero, vamos a crear una base de datos que conecta movieId al título de la película:

movie_titles <- movielens |>
  select(movieId, title) |>
  distinct()

Aquí están las 10 mejores películas según nuestro estimador:

movie_avgs |> left_join(movie_titles, by="movieId") |>
  arrange(desc(b_i)) |>
  slice(1:10) |>
  pull(title)
#>  [1] "When Night Is Falling"                                  
#>  [2] "Lamerica"                                               
#>  [3] "Mute Witness"                                           
#>  [4] "Picture Bride (Bijo photo)"                             
#>  [5] "Red Firecracker, Green Firecracker (Pao Da Shuang Deng)"
#>  [6] "Paris, France"                                          
#>  [7] "Faces"                                                  
#>  [8] "Maya Lin: A Strong Clear Vision"                        
#>  [9] "Heavy"                                                  
#> [10] "Gate of Heavenly Peace, The"

Y aquí están las 10 peores:

movie_avgs |> left_join(movie_titles, by="movieId") |>
  arrange(b_i) |>
  slice(1:10) |>
  pull(title)
#>  [1] "Children of the Corn IV: The Gathering"           
#>  [2] "Barney's Great Adventure"                         
#>  [3] "Merry War, A"                                     
#>  [4] "Whiteboyz"                                        
#>  [5] "Catfish in Black Bean Sauce"                      
#>  [6] "Killer Shrews, The"                               
#>  [7] "Horrors of Spider Island (Ein Toter Hing im Netz)"
#>  [8] "Monkeybone"                                       
#>  [9] "Arthur 2: On the Rocks"                           
#> [10] "Red Heat"

Todas parecen ser bastante desconocidas. Veamos con qué frecuencia se califican.

train_set |> count(movieId) |>
  left_join(movie_avgs, by="movieId") |>
  left_join(movie_titles, by="movieId") |>
  arrange(desc(b_i)) |>
  slice(1:10) |>
  pull(n)
#>  [1] 1 1 1 1 3 1 1 2 1 1

train_set |> count(movieId) |>
  left_join(movie_avgs) |>
  left_join(movie_titles, by="movieId") |>
  arrange(b_i) |>
  slice(1:10) |>
  pull(n)
#> Joining, by = "movieId"
#>  [1] 1 1 1 1 1 1 1 1 1 1

Las supuestas películas “mejores” y “peores” fueron calificadas por muy pocos usuarios, en la mayoría de los casos por solo 1. Estas películas son en su mayoría desconocidas. Esto se debe a que con solo unos pocos usuarios, tenemos más incertidumbre. Por lo tanto, mayores estimadores de \(b_i\), negativo o positivo, son más probables.

Estos son estimadores ruidosos en los que no debemos confiar, especialmente cuando se trata de predicciones. Grandes errores pueden aumentar nuestro RMSE, por lo que preferimos ser conservadores cuando no estamos seguros.

En secciones anteriores, calculamos el error estándar y construimos intervalos de confianza para tomar en cuenta los diferentes niveles de incertidumbre. Sin embargo, al hacer predicciones, necesitamos un número, una predicción, no un intervalo. Para esto, presentamos el concepto de regularización.

La regularización nos permite penalizar estimadores más grandes que se forman utilizando pequeños tamaños de muestra. Tienen puntos en común con el enfoque bayesiano que redujo las predicciones descritas en la Sección 16.4.

33.9.2 Mínimos cuadrados penalizados

La idea general detrás de la regularización es restringir la variabilidad total de los tamaños del efecto. ¿Por qué esto ayuda? Consideren un caso en el que tenemos película \(i=1\) con 100 clasificaciones de usuarios y 4 películas \(i=2,3,4,5\) con solo una calificación de usuario. Tenemos la intención de ajustar el modelo:

\[ Y_{u,i} = \mu + b_i + \varepsilon_{u,i} \]

Supongan que sabemos que la calificación promedio es, digamos, \(\mu = 3\). Si usamos mínimos cuadrados, el estimador para el primer efecto de película \(b_1\) es el promedio de las 100 calificaciones de los usuarios, \(1/100 \sum_{i=1}^{100} (Y_{i,1} - \mu)\), que esperamos sea bastante preciso. Sin embargo, el estimador para las películas 2, 3, 4 y 5 será simplemente la desviación observada de la calificación promedio \(\hat{b}_i = Y_{u,i} - \hat{\mu}\). Pero esto es un estimador basado en un solo número, por lo cual no será preciso. Tengan en cuenta que estos estimadores hacen el error \(Y_{u,i} - \mu + \hat{b}_i\) igual a 0 para \(i=2,3,4,5\), pero este es un caso de sobreentrenamiento. De hecho, ignorando al único usuario y adivinando que las películas 2, 3, 4 y 5 son solo películas promedio (\(b_i = 0\)) podría ofrecer una mejor predicción. La idea general de la regresión penalizada es controlar la variabilidad total de los efectos de la película: \(\sum_{i=1}^5 b_i^2\). Específicamente, en lugar de minimizar la ecuación de mínimos cuadrados, minimizamos una ecuación que añade una penalización:

\[\sum_{u,i} \left(y_{u,i} - \mu - b_i\right)^2 + \lambda \sum_{i} b_i^2\]

El primer término es solo la suma de errores cuadrados y el segundo es una penalización que aumenta cuando muchos \(b_i\) son grandes. Usando cálculo, podemos mostrar que los valores de \(b_i\) que minimizan esta ecuación son:

\[ \hat{b}_i(\lambda) = \frac{1}{\lambda + n_i} \sum_{u=1}^{n_i} \left(Y_{u,i} - \hat{\mu}\right) \]

dónde \(n_i\) es la cantidad de clasificaciones hechas para la película \(i\). Este enfoque tendrá el efecto deseado: cuando nuestro tamaño de muestra \(n_i\) es muy grande, un caso que nos dará un estimador estable, entonces la penalización \(\lambda\) es efectivamente ignorada ya que \(n_i+\lambda \approx n_i\). Sin embargo, cuando el \(n_i\) es pequeño, entonces el estimador \(\hat{b}_i(\lambda)\) se encoge hacia 0. Entre más grande \(\lambda\), más nos encogemos.

Calculemos estos estimadores regularizados de \(b_i\) utilizando \(\lambda=3\). Más adelante, veremos por qué elegimos 3.

lambda <- 3
mu <- mean(train_set$rating)
movie_reg_avgs <- train_set |>
  group_by(movieId) |>
  summarize(b_i = sum(rating - mu)/(n()+lambda), n_i = n())

Para ver cómo se reducen los estimadores, hagamos un gráfico de los estimadores regularizados versus los estimadores de mínimos cuadrados.

tibble(original = movie_avgs$b_i,
       regularlized = movie_reg_avgs$b_i,
       n = movie_reg_avgs$n_i) |>
  ggplot(aes(original, regularlized, size=sqrt(n))) +
  geom_point(shape=1, alpha=0.5)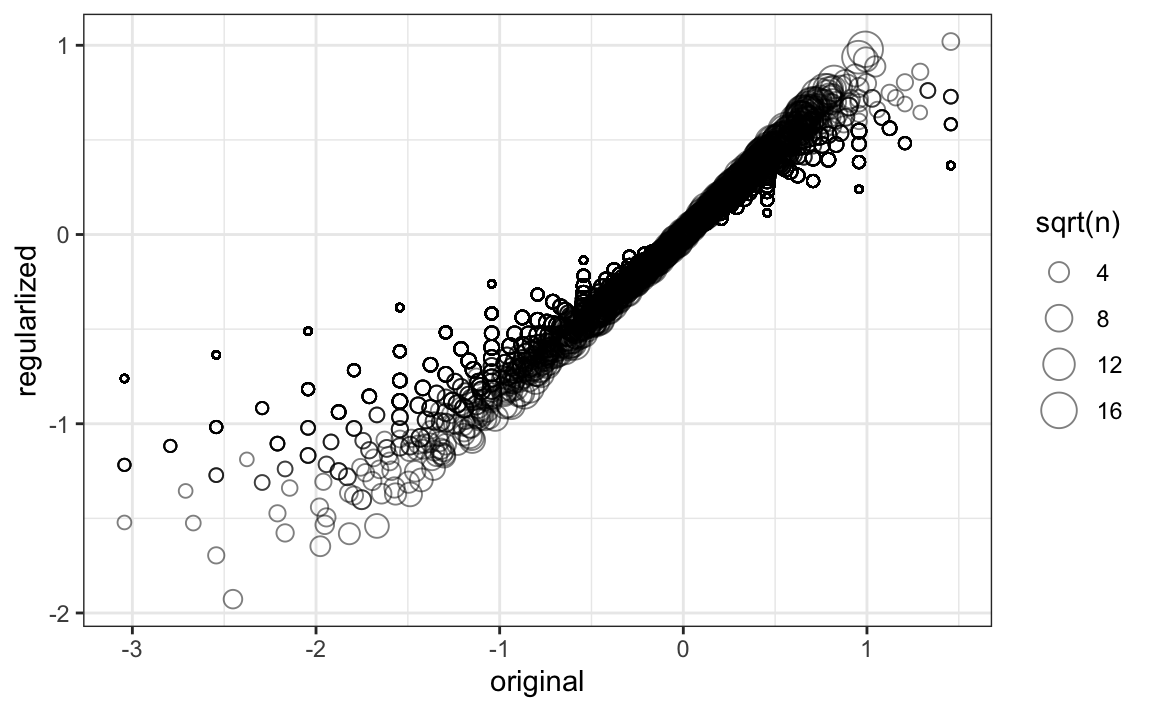

Ahora, echemos un vistazo a las 10 mejores películas según los estimadores penalizados \(\hat{b}_i(\lambda)\):

train_set |>
  count(movieId) |>
  left_join(movie_reg_avgs, by = "movieId") |>
  left_join(movie_titles, by = "movieId") |>
  arrange(desc(b_i)) |>
  slice(1:10) |>
  pull(title)
#>  [1] "Paris Is Burning"          "Shawshank Redemption, The"
#>  [3] "Godfather, The"            "African Queen, The"       
#>  [5] "Band of Brothers"          "Paperman"                 
#>  [7] "On the Waterfront"         "All About Eve"            
#>  [9] "Usual Suspects, The"       "Ikiru"

¡Esto tiene mucho más sentido! Estas películas son más populares y tienen más calificaciones. Aquí están las 10 peores películas:

train_set |>
  count(movieId) |>
  left_join(movie_reg_avgs, by = "movieId") |>
  left_join(movie_titles, by="movieId") |>
  arrange(b_i) |>
  select(title, b_i, n) |>
  slice(1:10) |>
  pull(title)
#>  [1] "Battlefield Earth"                      
#>  [2] "Joe's Apartment"                        
#>  [3] "Super Mario Bros."                      
#>  [4] "Speed 2: Cruise Control"                
#>  [5] "Dungeons & Dragons"                     
#>  [6] "Batman & Robin"                         
#>  [7] "Police Academy 6: City Under Siege"     
#>  [8] "Cats & Dogs"                            
#>  [9] "Disaster Movie"                         
#> [10] "Mighty Morphin Power Rangers: The Movie"

¿Mejoramos nuestros resultados?

predicted_ratings <- test_set |>
  left_join(movie_reg_avgs, by = "movieId") |>
  mutate(pred = mu + b_i) |>
  pull(pred)
RMSE(predicted_ratings, test_set$rating)
#> [1] 0.97

#> # A tibble: 4 × 2
#>   method                          RMSE
#>   <chr>                          <dbl>
#> 1 Just the average               1.05 
#> 2 Movie Effect Model             0.989
#> 3 Movie + User Effects Model     0.905
#> 4 Regularized Movie Effect Model 0.970

Los estimadores penalizados ofrecen una gran mejora sobre los estimadores de mínimos cuadrados.

33.9.3 Cómo elegir los términos de penalización

Noten que \(\lambda\) es un parámetro de ajuste. Podemos usar validación cruzada para elegirlo.

lambdas <- seq(0, 10, 0.25)

mu <- mean(train_set$rating)
just_the_sum <- train_set |>
  group_by(movieId) |>
  summarize(s = sum(rating - mu), n_i = n())

rmses <- sapply(lambdas, function(l){
  predicted_ratings <- test_set |>
    left_join(just_the_sum, by='movieId') |>
    mutate(b_i = s/(n_i+l)) |>
    mutate(pred = mu + b_i) |>
    pull(pred)
  return(RMSE(predicted_ratings, test_set$rating))
})
qplot(lambdas, rmses)
lambdas[which.min(rmses)]
#> [1] 3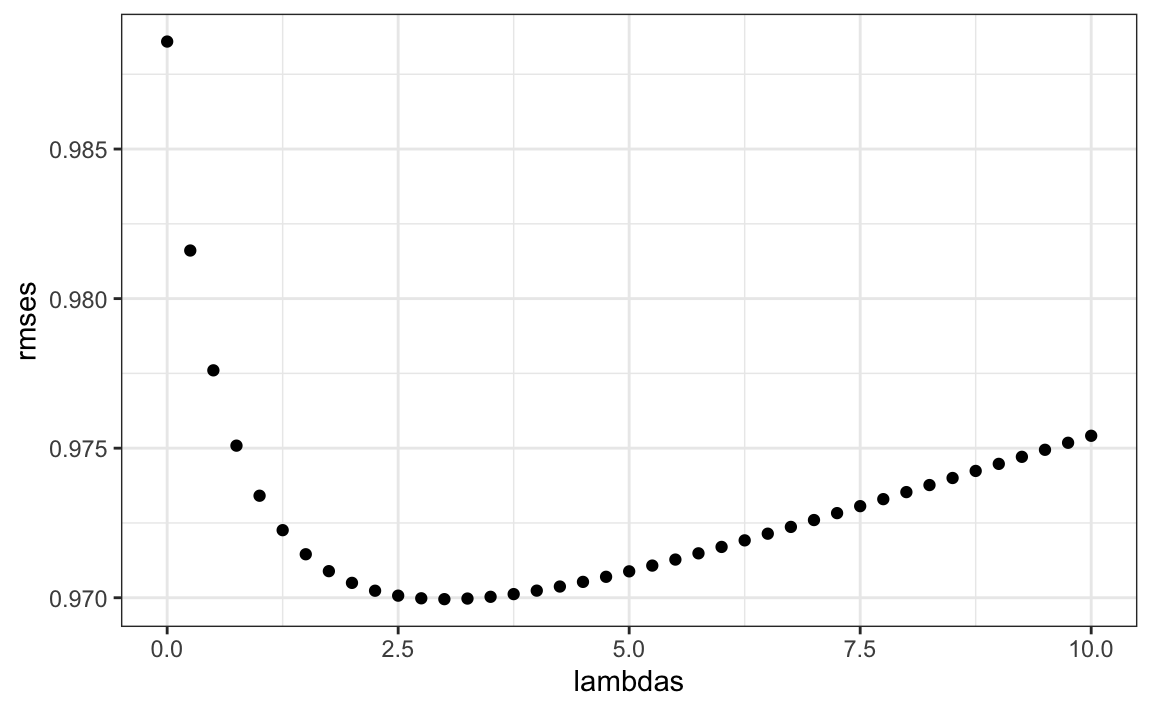

Sin embargo, si bien mostramos esto como una ilustración, en la práctica deberíamos usar validación cruzada completa solo en el set de entrenamiento, sin usar el set de evaluación hasta la evaluación final. El set de evaluación nunca debe utilizarse para el ajustamiento.

También podemos utilizar la regularización para estimar los efectos del usuario. Estamos minimizando:

\[ \sum_{u,i} \left(y_{u,i} - \mu - b_i - b_u \right)^2 + \lambda \left(\sum_{i} b_i^2 + \sum_{u} b_u^2\right) \]

Los estimadores que minimizan esto se pueden encontrar de manera similar a lo que hicimos anteriormente. Aquí usamos validación cruzada para elegir un \(\lambda\):

lambdas <- seq(0, 10, 0.25)

rmses <- sapply(lambdas, function(l){
  
  mu <- mean(train_set$rating)
  
  b_i <- train_set |>
    group_by(movieId) |>
    summarize(b_i = sum(rating - mu)/(n()+l))
  
  b_u <- train_set |>
    left_join(b_i, by="movieId") |>
    group_by(userId) |>
    summarize(b_u = sum(rating - b_i - mu)/(n()+l))
  
  predicted_ratings <-
    test_set |>
    left_join(b_i, by = "movieId") |>
    left_join(b_u, by = "userId") |>
    mutate(pred = mu + b_i + b_u) |>
    pull(pred)
  
  return(RMSE(predicted_ratings, test_set$rating))
})

qplot(lambdas, rmses)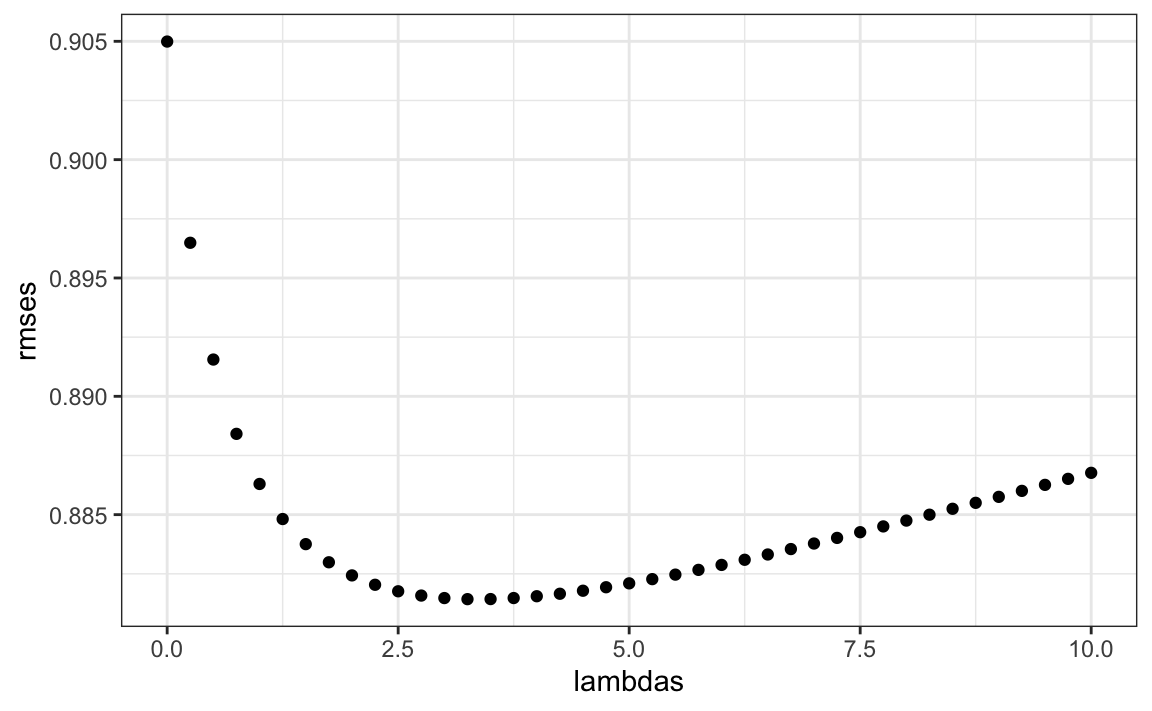

Para el modelo completo, el \(\lambda\) óptimo es:

lambda <- lambdas[which.min(rmses)]
lambda
#> [1] 3.25

method	RMSE
Just the average	1.053
Movie Effect Model	0.989
Movie + User Effects Model	0.905
Regularized Movie Effect Model	0.970
Regularized Movie + User Effect Model	0.881

33.10 Ejercicios

Un experto en educación aboga por escuelas más pequeñas. El experto basa esta recomendación en el hecho de que entre las mejores escuelas, muchas son escuelas pequeñas. Simulemos un set de datos para 100 escuelas. Primero, simulemos el número de estudiantes en cada escuela.

set.seed(1986)
n <- round(2^rnorm(1000, 8, 1))

Ahora asignemos una calidad verdadera para cada escuela completamente independiente del tamaño. Este es el parámetro que queremos estimar.

mu <- round(80 + 2 * rt(1000, 5))
range(mu)
schools <- data.frame(id = paste("PS",1:100),
                      size = n,
                      quality = mu,
                      rank = rank(-mu))

Podemos ver que las 10 mejores escuelas son:

schools |> top_n(10, quality) |> arrange(desc(quality))

Ahora hagamos que los estudiantes en la escuela tomen un examen. Existe una variabilidad aleatoria en la toma de exámenes, por lo que simularemos las puntuaciones de los exámenes distribuidos normalmente con el promedio determinado por la calidad de la escuela y las desviaciones estándar de 30 puntos porcentuales:

scores <- sapply(1:nrow(schools), function(i){
  scores <- rnorm(schools$size[i], schools$quality[i], 30)
  scores
})
schools <- schools |> mutate(score = sapply(scores, mean))

1. ¿Cuáles son las mejores escuelas según la puntuación promedio? Muestre solo la identificación, el tamaño y la puntuación promedio.

2. Compare el tamaño medio de la escuela con el tamaño medio de las 10 mejores escuelas según la puntuación.

3. Según esta prueba, parece que las escuelas pequeñas son mejores que las grandes. Cinco de las 10 mejores escuelas tienen 100 estudiantes o menos. ¿Pero cómo puede ser ésto? Construimos la simulación para que la calidad y el tamaño sean independientes. Repita el ejercicio para las peores 10 escuelas.

4. ¡Lo mismo es cierto para las peores escuelas! También son pequeñas. Grafique la puntuación promedio versus el tamaño de la escuela para ver qué está pasando. Destaque las 10 mejores escuelas según la calidad verdadera. Use la transformación de escala logarítmica para el tamaño.

5. Podemos ver que el error estándar de la puntuación tiene una mayor variabilidad cuando la escuela es más pequeña. Esta es una realidad estadística básica que aprendimos en las secciones de probabilidad e inferencia. De hecho, noten que 4 de las 10 mejores escuelas se encuentran en las 10 mejores escuelas según la puntuación del examen.

Usemos la regularización para elegir las mejores escuelas. Recuerde que la regularización encoge las desviaciones del promedio hacia 0. Entonces para aplicar la regularización aquí, primero debemos definir el promedio general para todas las escuelas:

overall <- mean(sapply(scores, mean))

y luego definir, para cada escuela, cómo se desvía de ese promedio. Escriba un código que calcule la puntuación por encima del promedio de cada escuela pero dividiéndolo por \(n + \lambda\) en lugar de \(n\), con \(n\) el tamaño de la escuela y \(\lambda\) un parámetro de regularización. Intente con \(\lambda = 3\).

6. Noten que esto mejora un poco las cosas. El número de escuelas pequeñas que no figuran entre las mejores ahora es 4. ¿Existe un \(\lambda\) mejor? Encuentre el \(\lambda\) que minimiza el RMSE = \(1/100 \sum_{i=1}^{100} (\mbox{quality} - \mbox{estimate})^2\).

7. Clasifique las escuelas según el promedio obtenido con los mejores \(\alpha\). Tengan en cuenta que ninguna escuela pequeña se incluye incorrectamente.

8. Un error común al usar la regularización es reducir los valores hacia 0 que no están centrados alrededor de 0. Por ejemplo, si no restamos el promedio general antes de reducir, obtenemos un resultado muy similar. Confirme esto volviendo a ejecutar el código del ejercicio 6, pero sin eliminar la media general.

33.11 Factorización de matrices

La factorización de matrices es un concepto ampliamente utilizado en machine learning. Está muy relacionado con el análisis de factores, la descomposición de valores singulares (singular value decomposition o SVD por sus siglas en inglés) y el análisis de componentes principales (PCA). Aquí describimos el concepto en el contexto de los sistemas de recomendación de películas.

Hemos descrito cómo el modelo:

\[ Y_{u,i} = \mu + b_i + b_u + \varepsilon_{u,i} \]

explica las diferencias de película a película a través de la \(b_i\) y las diferencias de usuario a usuario a través de la \(b_u\). Pero este modelo omite una fuente importante de variación relacionada con el hecho de que los grupos de películas tienen patrones de calificación similares y los grupos de usuarios también tienen patrones de calificación similares. Descubriremos estos patrones estudiando los residuos:

\[ r_{u,i} = y_{u,i} - \hat{b}_i - \hat{b}_u \]

Para ver esto, convertiremos los datos en una matriz para que cada usuario obtenga una fila, cada película obtenga una columna y \(y_{u,i}\) sea la entrada en fila \(u\) y columna \(i\). Con fines ilustrativos, solo consideraremos un pequeño subconjunto de películas con muchas calificaciones y usuarios que han calificado muchas películas. También incluímos Scent of a Woman (movieId == 3252) porque la usamos para un ejemplo específico:

train_small <- movielens |>
  group_by(movieId) |>
  filter(n() >= 50 | movieId == 3252) |> ungroup() |>
  group_by(userId) |>
  filter(n() >= 50) |> ungroup()

y <- train_small |> 
  select(userId, movieId, rating) |>
  pivot_wider(names_from = "movieId", values_from = "rating") |>
  as.matrix()

Agregamos nombres de fila y columna:

rownames(y)<- y[,1]
y <- y[,-1]

movie_titles <- movielens |>
  select(movieId, title) |>
  distinct()

colnames(y) <- with(movie_titles, title[match(colnames(y), movieId)])

y los convertimos en residuos eliminando los efectos de columna y fila:

y <- sweep(y, 2, colMeans(y, na.rm=TRUE))
y <- sweep(y, 1, rowMeans(y, na.rm=TRUE))

Si el modelo anterior explica todas las señales, y los \(\varepsilon\) son solo ruido, entonces los residuos para diferentes películas deben ser independientes entre sí. Pero no lo son. Aquí hay unos ejemplos:

m_1 <- "Godfather, The"
m_2 <- "Godfather: Part II, The"
p1 <- qplot(y[ ,m_1], y[,m_2], xlab = m_1, ylab = m_2)

m_1 <- "Godfather, The"
m_3 <- "Goodfellas"
p2 <- qplot(y[ ,m_1], y[,m_3], xlab = m_1, ylab = m_3)

m_4 <- "You've Got Mail"
m_5 <- "Sleepless in Seattle"
p3 <- qplot(y[ ,m_4], y[,m_5], xlab = m_4, ylab = m_5)

gridExtra::grid.arrange(p1, p2 ,p3, ncol = 3)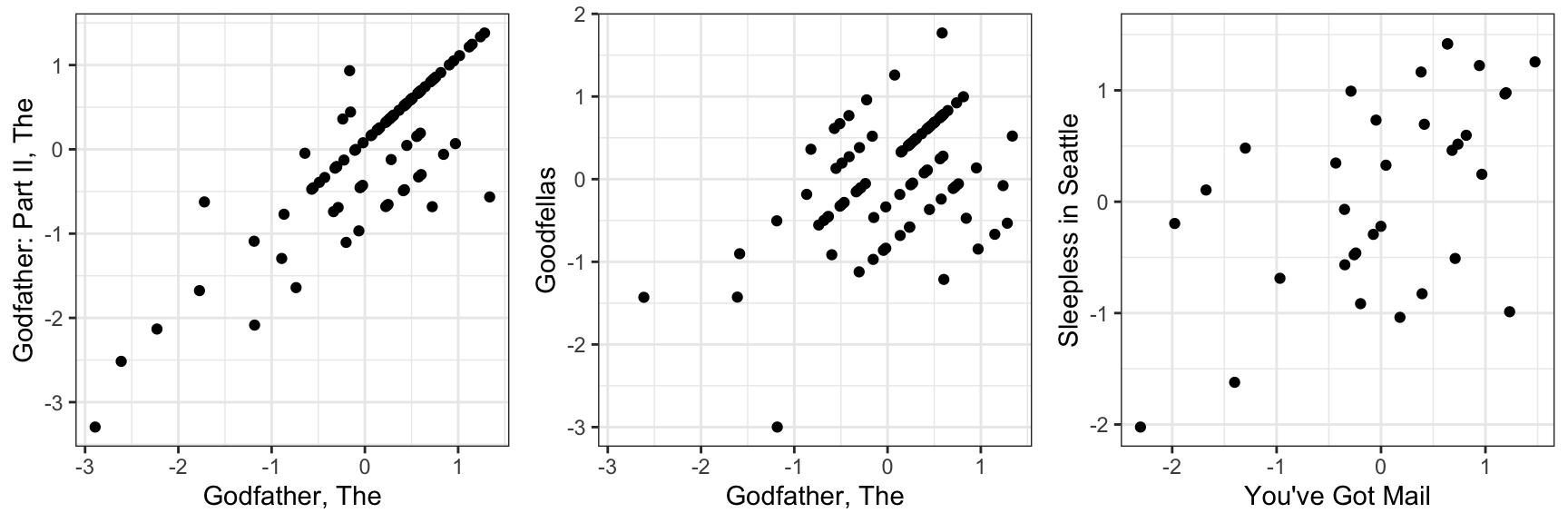

Estos gráficos muestran que a los usuarios que les gustó The Godfather más de lo que el modelo espera de ellos, según la película y los efectos del usuario, también les gustó The Godfather II más de lo esperado. Se observa una relación similar al comparar The Godfather y Goodfellas. Aunque no es tan fuerte, todavía hay correlación. También vemos correlaciones entre You’ve Got Mail y Sleepless in Seattle.

Al observar la correlación entre películas, podemos ver un patrón (cambiamos los nombres de las columnas para ahorrar espacio de impresión):

x <- y[, c(m_1, m_2, m_3, m_4, m_5)]
short_names <- c("Godfather", "Godfather2", "Goodfellas",
                 "You've Got", "Sleepless")
colnames(x) <- short_names
cor(x, use="pairwise.complete")
#>            Godfather Godfather2 Goodfellas You've Got Sleepless
#> Godfather      1.000      0.829      0.444     -0.440    -0.378
#> Godfather2     0.829      1.000      0.521     -0.331    -0.358
#> Goodfellas     0.444      0.521      1.000     -0.481    -0.402
#> You've Got    -0.440     -0.331     -0.481      1.000     0.533
#> Sleepless     -0.378     -0.358     -0.402      0.533     1.000

Parece que hay personas a las que les gustan las comedias románticas más de lo esperado, mientras que hay otras personas a las que les gustan las películas de gángsters más de lo esperado.

Estos resultados nos dicen que hay estructura en los datos. Pero, ¿cómo podemos modelar esto?

33.11.1 Análisis de factores

Aquí hay una ilustración, usando una simulación, de cómo podemos usar un poco de estructura para predecir el \(r_{u,i}\). Supongan que nuestros residuos r se ven así:

round(r, 1)
#>    Godfather Godfather2 Goodfellas You've Got Sleepless
#> 1        2.0        2.3        2.2       -1.8      -1.9
#> 2        2.0        1.7        2.0       -1.9      -1.7
#> 3        1.9        2.4        2.1       -2.3      -2.0
#> 4       -0.3        0.3        0.3       -0.4      -0.3
#> 5       -0.3       -0.4        0.3        0.2       0.3
#> 6       -0.1        0.1        0.2       -0.3       0.2
#> 7       -0.1        0.0       -0.2       -0.2       0.3
#> 8        0.2        0.2        0.1        0.0       0.4
#> 9       -1.7       -2.1       -1.8        2.0       2.4
#> 10      -2.3       -1.8       -1.7        1.8       1.7
#> 11      -1.7       -2.0       -2.1        1.9       2.3
#> 12      -1.8       -1.7       -2.1        2.3       2.0

Parece que hay un patrón aquí. De hecho, podemos ver patrones de correlación muy fuertes:

cor(r)
#>            Godfather Godfather2 Goodfellas You've Got Sleepless
#> Godfather      1.000      0.980      0.978     -0.974    -0.966
#> Godfather2     0.980      1.000      0.983     -0.987    -0.992
#> Goodfellas     0.978      0.983      1.000     -0.986    -0.989
#> You've Got    -0.974     -0.987     -0.986      1.000     0.986
#> Sleepless     -0.966     -0.992     -0.989      0.986     1.000

Podemos crear vectores q y p, que pueden explicar gran parte de la estructura que vemos. Los q se verían así:

t(q)
#>      Godfather Godfather2 Goodfellas You've Got Sleepless
#> [1,]         1          1          1         -1        -1

y reduce las películas a dos grupos: gángster (codificado con 1) y romance (codificado con -1). También podemos reducir los usuarios a tres grupos:

t(p)
#>      1 2 3 4 5 6 7 8  9 10 11 12
#> [1,] 2 2 2 0 0 0 0 0 -2 -2 -2 -2

los que les gustan las películas de gángsters y no les gustan las películas románticas (codificadas como 2), los que les gustan las películas románticas y no les gustan las películas de gángsters (codificadas como -2), y los que no les importa (codificadas como 0). El punto principal aquí es que casi podemos reconstruir \(r\), que tiene 60 valores, con un par de vectores que totalizan 17 valores. Noten que p y q son equivalentes a los patrones y pesos que describimos en la Sección 33.5.4.

Si \(r\) contiene los residuos para usuarios \(u=1,\dots,12\) para peliculas \(i=1,\dots,5\), podemos escribir la siguiente fórmula matemática para nuestros residuos \(r_{u,i}\).

\[ r_{u,i} \approx p_u q_i \] Esto implica que podemos explicar más variabilidad modificando nuestro modelo anterior para recomendaciones de películas a:

\[ Y_{u,i} = \mu + b_i + b_u + p_u q_i + \varepsilon_{u,i} \]

Sin embargo, motivamos la necesidad del término \(p_u q_i\) con una simulación sencilla. La estructura que se encuentra en los datos suele ser más compleja. Por ejemplo, en esta primera simulación supusimos que solo había un factor \(p_u\) que determinaba a cuál de las dos películas de géneros \(u\) pertenece. Pero la estructura en nuestros datos de películas parece ser mucho más complicada que las películas de gángsters versus las románticas. Podemos tener muchos otros factores. Aquí presentamos una simulación un poco más compleja. Ahora agregamos una sexta película.

round(r, 1)
#>    Godfather Godfather2 Goodfellas You've Got Sleepless Scent
#> 1        0.5        0.6        1.6       -0.5      -0.5  -1.6
#> 2        1.5        1.4        0.5       -1.5      -1.4  -0.4
#> 3        1.5        1.6        0.5       -1.6      -1.5  -0.5
#> 4       -0.1        0.1        0.1       -0.1      -0.1   0.1
#> 5       -0.1       -0.1        0.1        0.0       0.1  -0.1
#> 6        0.5        0.5       -0.4       -0.6      -0.5   0.5
#> 7        0.5        0.5       -0.5       -0.6      -0.4   0.4
#> 8        0.5        0.6       -0.5       -0.5      -0.4   0.4
#> 9       -0.9       -1.0       -0.9        1.0       1.1   0.9
#> 10      -1.6       -1.4       -0.4        1.5       1.4   0.5
#> 11      -1.4       -1.5       -0.5        1.5       1.6   0.6
#> 12      -1.4       -1.4       -0.5        1.6       1.5   0.6

Al explorar la estructura de correlación de este nuevo set de datos:

colnames(r)[4:6] <- c("YGM", "SS", "SW")
cor(r)
#>            Godfather Godfather2 Goodfellas    YGM     SS     SW
#> Godfather      1.000      0.997      0.562 -0.997 -0.996 -0.571
#> Godfather2     0.997      1.000      0.577 -0.998 -0.999 -0.583
#> Goodfellas     0.562      0.577      1.000 -0.552 -0.583 -0.994
#> YGM           -0.997     -0.998     -0.552  1.000  0.998  0.558
#> SS            -0.996     -0.999     -0.583  0.998  1.000  0.588
#> SW            -0.571     -0.583     -0.994  0.558  0.588  1.000

notamos que quizás necesitamos un segundo factor para tomar en cuenta el hecho de que a algunos usuarios les gusta Al Pacino, mientras que a otros no les gusta o no les importa. Observen que la estructura general de la correlación obtenida de los datos simulados no está tan lejos de la correlación real:

six_movies <- c(m_1, m_2, m_3, m_4, m_5, m_6)
x <- y[, six_movies]
colnames(x) <- colnames(r)
cor(x, use="pairwise.complete")
#>            Godfather Godfather2 Goodfellas    YGM     SS      SW
#> Godfather     1.0000      0.829      0.444 -0.440 -0.378  0.0589
#> Godfather2    0.8285      1.000      0.521 -0.331 -0.358  0.1186
#> Goodfellas    0.4441      0.521      1.000 -0.481 -0.402 -0.1230
#> YGM          -0.4397     -0.331     -0.481  1.000  0.533 -0.1699
#> SS           -0.3781     -0.358     -0.402  0.533  1.000 -0.1822
#> SW            0.0589      0.119     -0.123 -0.170 -0.182  1.0000

Para explicar esta estructura más complicada, necesitamos dos factores. Por ejemplo, algo como lo siguiente:

t(q)
#>      Godfather Godfather2 Goodfellas You've Got Sleepless Scent
#> [1,]         1          1          1         -1        -1    -1
#> [2,]         1          1         -1         -1        -1     1

con el primer factor (la primera fila) utilizado para codificar las películas de gángster versus las películas románticas y un segundo factor (la segunda fila) para explicar los grupos de películas con Al Pacino versus los grupos sin Al Pacino. También necesitaremos dos sets de coeficientes para explicar la variabilidad introducida por los tipos de grupos \(3\times 3\):

t(p)
#>         1   2   3 4 5   6   7   8  9   10   11   12
#> [1,]  1.0 1.0 1.0 0 0 0.0 0.0 0.0 -1 -1.0 -1.0 -1.0
#> [2,] -0.5 0.5 0.5 0 0 0.5 0.5 0.5  0 -0.5 -0.5 -0.5

El modelo con dos factores tiene 36 parámetros que se pueden usar para explicar gran parte de la variabilidad en las 72 clasificaciones:

\[ Y_{u,i} = \mu + b_i + b_u + p_{u,1} q_{1,i} + p_{u,2} q_{2,i} + \varepsilon_{u,i} \]

Tengan en cuenta que en una aplicación de datos real, necesitamos ajustar este modelo a los datos. Para explicar la correlación compleja que observamos en datos reales, generalmente permitimos que las entradas de \(p\) y \(q\) sean valores continuos, en lugar de discretos como las que usamos en la simulación. Por ejemplo, en lugar de dividir las películas en gángster o romance, definimos un continuo. Además, recuerden que este no es un modelo lineal y para ajustarlo necesitamos usar un algoritmo diferente a ese usado por lm para encontrar los parámetros que minimizan los mínimos cuadrados. Los algoritmos ganadores del Netflix challenge ajustaron un modelo similar al anterior y utilizaron la regularización para penalizar por grandes valores de \(p\) y \(q\), en lugar de usar mínimos cuadrados. Implementar este enfoque está más allá del alcance de este libro.

33.11.2 Conexión a SVD y PCA

La descomposición:

\[ r_{u,i} \approx p_{u,1} q_{1,i} + p_{u,2} q_{2,i} \]

está muy relacionada a SVD y PCA. SVD y PCA son conceptos complicados, pero una forma de entenderlos es que SVD es un algoritmo que encuentra los vectores \(p\) y \(q\) que nos permiten reescribir la matriz \(\mbox{r}\) con \(m\) filas y \(n\) columnas como:

\[ r_{u,i} = p_{u,1} q_{1,i} + p_{u,2} q_{2,i} + \dots + p_{u,n} q_{n,i} \]

con la variabilidad de cada término disminuyendo y con las \(p\)s no correlacionadas. El algoritmo también calcula esta variabilidad para que podamos saber cuánta de la variabilidad total de las matrices se explica a medida que vayamos agregando nuevos términos. Esto nos deja ver que, con solo unos pocos términos, podemos explicar la mayor parte de la variabilidad.

Veamos un ejemplo con los datos de la película. Para calcular la descomposición, haremos que los residuos con NAs sean iguales a 0:

y[is.na(y)] <- 0
pca <- prcomp(y)

Los vectores \(q\) se denominan componentes principales y se almacenan en esta matriz:

dim(pca$rotation)
#> [1] 454 292

Mientras que la \(p\), o los efectos del usuario, están aquí:

dim(pca$x)
#> [1] 292 292

Podemos ver la variabilidad de cada uno de los vectores:

qplot(1:nrow(x), pca$sdev, xlab = "PC")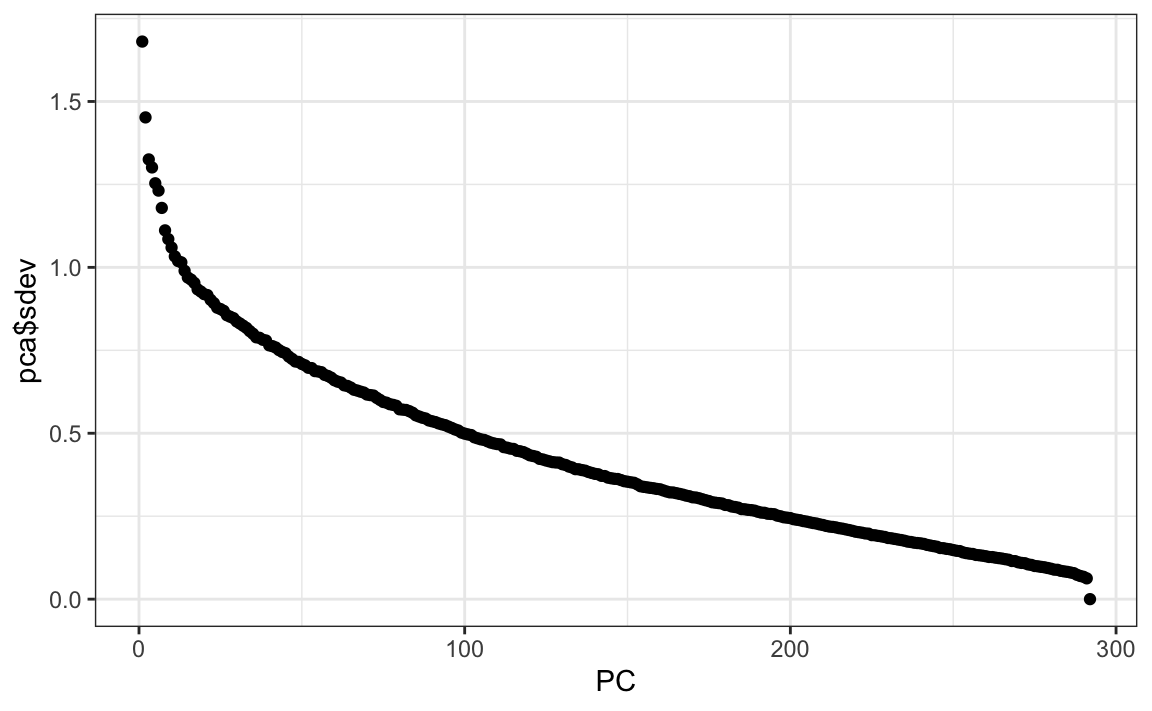

También notamos que los dos primeros componentes principales están relacionados a la estructura en las opiniones sobre películas:

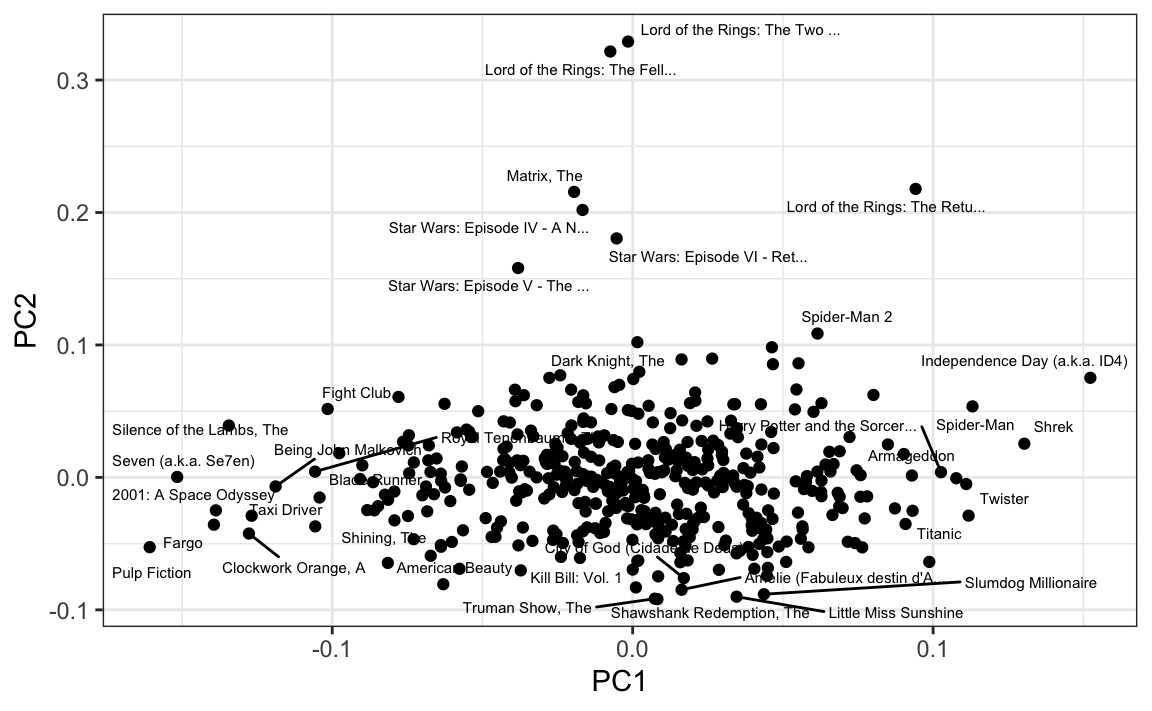
Con solo mirar los 10 primeros en cada dirección, vemos un patrón significativo. El primer PC muestra la diferencia entre las películas aclamadas por la crítica en un lado:

#>  [1] "Pulp Fiction"              "Seven (a.k.a. Se7en)"     
#>  [3] "Fargo"                     "2001: A Space Odyssey"    
#>  [5] "Silence of the Lambs, The" "Clockwork Orange, A"      
#>  [7] "Taxi Driver"               "Being John Malkovich"     
#>  [9] "Royal Tenenbaums, The"     "Shining, The"

y los éxitos de taquilla de Hollywood en otro:

#>  [1] "Independence Day (a.k.a. ID4)"  "Shrek"                         
#>  [3] "Spider-Man"                     "Titanic"                       
#>  [5] "Twister"                        "Armageddon"                    
#>  [7] "Harry Potter and the Sorcer..." "Forrest Gump"                  
#>  [9] "Lord of the Rings: The Retu..." "Enemy of the State"

Mientras que el segundo PC parece ir de películas artísticas e independientes:

#>  [1] "Shawshank Redemption, The"      "Truman Show, The"              
#>  [3] "Little Miss Sunshine"           "Slumdog Millionaire"           
#>  [5] "Amelie (Fabuleux destin d'A..." "Kill Bill: Vol. 1"             
#>  [7] "American Beauty"                "City of God (Cidade de Deus)"  
#>  [9] "Mars Attacks!"                  "Beautiful Mind, A"

hacia favoritas de los nerds:

#>  [1] "Lord of the Rings: The Two ..." "Lord of the Rings: The Fell..."
#>  [3] "Lord of the Rings: The Retu..." "Matrix, The"                   
#>  [5] "Star Wars: Episode IV - A N..." "Star Wars: Episode VI - Ret..."
#>  [7] "Star Wars: Episode V - The ..." "Spider-Man 2"                  
#>  [9] "Dark Knight, The"               "Speed"

Ajustar un modelo que incorpora estos estimadores es complicado. Para aquellos interesados en implementar un enfoque que incorpore estas ideas, recomendamos el paquete recommenderlab. Los detalles están más allá del alcance de este libro.

33.12 Ejercicios

En este set de ejercicios, trataremos un tema útil para comprender la factorización de matrices: la descomposición de valores singulares (singular value decomposition o SVD por sus siglas en inglés). SVD es un resultado matemático que se usa ampliamente en machine learning, tanto en la práctica como para comprender las propiedades matemáticas de algunos algoritmos. Este es un tema bastante avanzado y para completar este set de ejercicios tendrán que estar familiarizados con conceptos de álgebra lineal, como la multiplicación de matrices, las matrices ortogonales y las matrices diagonales.

El SVD nos dice que podemos descomponer un \(N\times p\) matriz \(Y\) con \(p < N\) como:

\[ Y = U D V^{\top} \]

con \(U\) y \(V\) ortogonal de dimensiones \(N\times p\) y \(p\times p\), respectivamente, y \(D\) un \(p \times p\) matriz diagonal con los valores de la diagonal decreciendo:

\[d_{1,1} \geq d_{2,2} \geq \dots d_{p,p}.\]

En este ejercicio, veremos una de las formas en que esta descomposición puede ser útil. Para hacer esto, construiremos un set de datos que representa las calificaciones de 100 estudiantes en 24 materias diferentes. El promedio general se ha eliminado, por lo que estos datos representan el punto porcentual que cada estudiante recibió por encima o por debajo de la puntuación promedio de la prueba. Entonces un 0 representa una calificación promedio (C), un 25 es una calificación alta (A +) y un -25 representa una calificación baja (F). Puede simular los datos de esta manera:

set.seed(1987)
n <- 100
k <- 8
Sigma <- 64 * matrix(c(1, .75, .5, .75, 1, .5, .5, .5, 1), 3, 3)
m <- MASS::mvrnorm(n, rep(0, 3), Sigma)
m <- m[order(rowMeans(m), decreasing = TRUE),]
y <- m %x% matrix(rep(1, k), nrow = 1) +
  matrix(rnorm(matrix(n * k * 3)), n, k * 3)
colnames(y) <- c(paste(rep("Math",k), 1:k, sep="_"),
                 paste(rep("Science",k), 1:k, sep="_"),
                 paste(rep("Arts",k), 1:k, sep="_"))

Nuestro objetivo es describir el desempeño de los estudiantes de la manera más sucinta posible. Por ejemplo, queremos saber si los resultados de estas pruebas son solo números independientes aleatorios. ¿Todos los estudiantes son igual de buenos? ¿Ser bueno en un tema implica ser bueno en otro? ¿Cómo ayuda el SVD con todo esto? Iremos paso a paso para mostrar que con solo tres pares relativamente pequeños de vectores podemos explicar gran parte de la variabilidad en este \(100 \times 24\) set de datos.

Puede visualizar las 24 puntuaciones de las pruebas para los 100 estudiantes al graficar una imagen:

my_image <- function(x, zlim = range(x), ...){
  colors = rev(RColorBrewer::brewer.pal(9, "RdBu"))
  cols <- 1:ncol(x)
  rows <- 1:nrow(x)
  image(cols, rows, t(x[rev(rows),,drop=FALSE]), xaxt = "n", yaxt = "n",
        xlab="", ylab="", col = colors, zlim = zlim, ...)
  abline(h=rows + 0.5, v = cols + 0.5)
  axis(side = 1, cols, colnames(x), las = 2)
}

my_image(y)

1. ¿Cómo describiría los datos basados en esta figura?

1. Las puntuaciones de las pruebas son independientes entre sí.
2. Los estudiantes que evalúan bien están en la parte superior de la imagen y parece que hay tres agrupaciones por materia.
3. Los estudiantes que son buenos en matemáticas no son buenos en ciencias.
4. Los estudiantes que son buenos en matemáticas no son buenos en humanidades.

2. Puede examinar la correlación entre las puntuaciones de la prueba directamente de esta manera:

my_image(cor(y), zlim = c(-1,1))
range(cor(y))
axis(side = 2, 1:ncol(y), rev(colnames(y)), las = 2)

¿Cuál de las siguientes opciones describe mejor lo que ve?

1. Las puntuaciones de las pruebas son independientes.
2. Las matemáticas y las ciencias están altamente correlacionadas, pero las humanidades no.
3. Existe una alta correlación entre las pruebas en la misma materia pero no hay correlación entre las materias.
4. Hay una correlación entre todas las pruebas, pero es mayor si las pruebas son de ciencias y matemáticas e incluso mayor dentro de cada materia.

3. Recuerde que la ortogonalidad significa que \(U^{\top}U\) y \(V^{\top}V\) son iguales a la matriz de identidad. Esto implica que también podemos reescribir la descomposición como:

\[ Y V = U D \mbox{ or } U^{\top}Y = D V^{\top}\]

Podemos pensar en \(YV\) y \(U^{\top}V\) como dos transformaciones de Y que preservan la variabilidad total de \(Y\) ya que \(U\) y \(V\) son ortogonales.

Use la función svd para calcular el SVD de y. Esta función devolverá \(U\), \(V\) y las entradas diagonales de \(D\).

s <- svd(y)
names(s)

Puede verificar que el SVD funciona al escribir:

y_svd <- s$u %*% diag(s$d) %*% t(s$v)
max(abs(y - y_svd))

Calcule la suma de cuadrados de las columnas de \(Y\) y guárdelas en ss_y. Luego calcule la suma de cuadrados de columnas del transformado \(YV\) y guárdelas en ss_yv. Confirme que sum(ss_y) es igual a sum(ss_yv).

4. Vemos que se conserva la suma total de cuadrados. Esto es porque \(V\) es ortogonal. Ahora para comenzar a entender cómo \(YV\) es útil, grafique ss_y contra el número de columna y luego haga lo mismo para ss_yv. ¿Qué observa?

5. Vemos que la variabilidad de las columnas de \(YV\) está disminuyendo. Además, vemos que, en relación con los tres primeros, la variabilidad de las columnas más allá del tercero es casi 0. Ahora observe que no tuvimos que calcular ss_yv porque ya tenemos la respuesta ¿Cómo? Recuerde que \(YV = UD\) y como \(U\) es ortogonal, sabemos que la suma de cuadrados de las columnas de \(UD\) son las entradas diagonales de \(D\) al cuadrado. Confirme esto graficando la raíz cuadrada de ss_yv versus las entradas diagonales de \(D\).

6. De lo anterior, sabemos que la suma de cuadrados de las columnas de \(Y\) (la suma total de cuadrados) se añade a la suma de s$d^2 y que la transformación \(YV\) nos da columnas con sumas de cuadrados iguales a s$d^2. Ahora calcule qué porcentaje de la variabilidad total se explica solo por las tres primeras columnas de \(YV\).

7. Vemos que casi el 99% de la variabilidad se explica por las primeras tres columnas de \(YV = UD\). Entonces esto implica que deberíamos poder explicar gran parte de la variabilidad y estructura que encontramos al explorar los datos con unas pocas columnas. Antes de continuar, vamos a mostrar un truco computacional útil para evitar crear la matriz diag(s$d). Para motivar esto, notamos que si escribimos \(U\) en sus columnas \([U_1, U_2,\dots, U_p]\), entonces \(UD\) es igual a:

\[UD = [U_1 d_{1,1}, U_2 d_{2,2}, \dots, U_p d_{p,p}]\]

Utilice la función sweep para calcular \(UD\) sin construir diag(s$d) y sin usar multiplicación de matrices.

8. Sabemos que \(U_1 d_{1,1}\), la primera columna de \(UD\), tiene la mayor variabilidad de todas las columnas de \(UD\). Anteriormente vimos una imagen de \(Y\):

my_image(y)

en la que podemos ver que la variabilidad de estudiante a estudiante es bastante grande y que parece que los estudiantes que son buenos en una materia son buenos en todas. Esto implica que el promedio (en todas las materias) de cada alumno debe explicar en gran medida la variabilidad. Calcule la puntuación promedio de cada estudiante y grafíquelo contra \(U_1 d_{1,1}\). Describa lo que encuentra.

9. Notamos que los signos en SVD son arbitrarios porque:

\[ U D V^{\top} = (-U) D (-V)^{\top} \]

Con esto en mente, vemos que la primera columna de \(UD\) es casi idéntica a la puntuación promedio de cada estudiante, excepto por el signo.

Esto implica que multiplicar \(Y\) por la primera columna de \(V\) debe realizar una operación similar a tomar el promedio. Haga un gráfico de imagen de \(V\) y describa la primera columna en relación con las otras y cómo se relaciona esto con tomar un promedio.

10. Ya vimos que podemos reescribir \(UD\) como:

\[U_1 d_{1,1} + U_2 d_{2,2} + \dots + U_p d_{p,p}\]

con \(U_j\) la columna j de \(U\). Esto implica que podemos reescribir todo el SVD como:

\[Y = U_1 d_{1,1} V_1 ^{\top} + U_2 d_{2,2} V_2 ^{\top} + \dots + U_p d_{p,p} V_p ^{\top}\]

con \(V_j\) la columna j de \(V\). Grafique \(U_1\), luego grafique \(V_1^{\top}\) usando el mismo rango para los límites del eje y, entonces haga una imagen de \(U_1 d_{1,1} V_1 ^{\top}\) y compárela con la imagen de \(Y\). Sugerencia: use la función my_image definida anteriormente y el argumento drop=FALSE para asegurar que los subconjuntos de matrices son matrices.

11. Vemos que con solo un vector de longitud 100, un escalar y un vector de longitud 24, nos acercamos a reconstruir la matriz \(100 \times 24\) original. Esta es nuestra primera factorización de matrices:

\[ Y \approx d_{1,1} U_1 V_1^{\top}\]

Sabemos que explica s $d[1]^2/sum(s$ d^2) * 100 por ciento de la variabilidad total. Nuestra aproximación solo explica la observación de que los buenos estudiantes tienden a ser buenos en todas las materias. Pero otro aspecto de los datos originales que nuestra aproximación no explica es la mayor similitud que observamos dentro de las materias. Podemos ver esto calculando la diferencia entre nuestra aproximación y los datos originales y luego calculando las correlaciones. Pueden ver esto ejecutando este código:

resid <- y - with(s,(u[,1, drop=FALSE]*d[1]) %*% t(v[,1, drop=FALSE]))
my_image(cor(resid), zlim = c(-1,1))
axis(side = 2, 1:ncol(y), rev(colnames(y)), las = 2)

Ahora que hemos eliminado el efecto general del estudiante, el gráfico de correlación revela que todavía no hemos explicado la correlación interna de la materia ni el hecho de que las puntuaciones en matemáticas y ciencias son más parecidas entre sí que a las puntuaciones en las artes. Así que exploremos la segunda columna del SVD. Repita el ejercicio anterior pero para la segunda columna: grafique \(U_2\), entonces grafique \(V_2^{\top}\) usando el mismo rango para los límites del eje y, finalmente haga una imagen de \(U_2 d_{2,2} V_2 ^{\top}\) y compárela con la imagen de resid.

12. La segunda columna se relaciona claramente con la diferencia de habilidad del estudiante en matemáticas/ciencias versus las artes. Podemos ver esto más claramente en el gráfico de s$v[,2]. Sumar las matrices resultantes usando estas dos columnas ayudará con nuestra aproximación:

\[ Y \approx d_{1,1} U_1 V_1^{\top} + d_{2,2} U_2 V_2^{\top} \]

Sabemos que explicará:

sum(s$d[1:2]^2)/sum(s$d^2) * 100

porcentaje de la variabilidad total. Podemos calcular nuevos residuos así:

resid <- y - with(s,sweep(u[,1:2], 2, d[1:2], FUN="*") %*% t(v[,1:2]))
my_image(cor(resid), zlim = c(-1,1))
axis(side = 2, 1:ncol(y), rev(colnames(y)), las = 2)

y ver que la estructura que queda es impulsada por las diferencias entre matemáticas y ciencias. Confirme esto graficando \(U_3\), luego grafique \(V_3^{\top}\) usando el mismo rango para los límites del eje y, luego haga una imagen de \(U_3 d_{3,3} V_3 ^{\top}\) y compárela con la imagen de resid.

13. La tercera columna se relaciona claramente con la diferencia de habilidad del estudiante en matemáticas y ciencias. Podemos ver esto más claramente en el gráfico de s$v[,3]. Agregar la matriz que obtenemos con estas dos columnas ayudará con nuestra aproximación:

\[ Y \approx d_{1,1} U_1 V_1^{\top} + d_{2,2} U_2 V_2^{\top} + d_{3,3} U_3 V_3^{\top}\]

Sabemos que explicará:

sum(s$d[1:3]^2)/sum(s$d^2) * 100

porcentaje de la variabilidad total. Podemos calcular nuevos residuos como este:

resid <- y - with(s,sweep(u[,1:3], 2, d[1:3], FUN="*") %*% t(v[,1:3]))
my_image(cor(resid), zlim = c(-1,1))
axis(side = 2, 1:ncol(y), rev(colnames(y)), las = 2)

Ya no vemos estructura en los residuos: parecen ser independientes entre sí. Esto implica que podemos describir los datos con el siguiente modelo:

\[ Y = d_{1,1} U_1 V_1^{\top} + d_{2,2} U_2 V_2^{\top} + d_{3,3} U_3 V_3^{\top} + \varepsilon\]

con \(\varepsilon\) una matriz de errores independientes idénticamente distribuidos. Este modelo es útil porque resumimos \(100 \times 24\) observaciones con \(3 \times (100+24+1) = 375\) números. Además, los tres componentes del modelo tienen interpretaciones útiles: 1) la capacidad general de un estudiante, 2) la diferencia en la habilidad entre las matemáticas/ciencias y las artes, y 3) las diferencias restantes entre las tres materias. Los tamaños \(d_{1,1}, d_{2,2}\) y \(d_{3,3}\) nos dicen la variabilidad explicada por cada componente. Finalmente, tengan en cuenta que los componentes \(d_{j,j} U_j V_j^{\top}\) son equivalentes al componente principal j.

Termine el ejercicio graficando una imagen de \(Y\), una imagen de \(d_{1,1} U_1 V_1^{\top} + d_{2,2} U_2 V_2^{\top} + d_{3,3} U_3 V_3^{\top}\) y una imagen de los residuos, todos con el mismo zlim.

14. Avanzado: El set de datos movielens incluido en el paquete dslabs es un pequeño subconjunto de un set de datos más grande con millones de clasificaciones. Puede encontrar el set de datos más reciente aquí: https://grouplens.org/datasets/movielens/20m/. Cree su propio sistema de recomendaciones utilizando todas las herramientas que le hemos mostrado.

---

120. http://bits.blogs.nytimes.com/2009/09/21/netflix-awards-1-million-prize-and-starts-a-new-contest/↩︎

121. https://grouplens.org/↩︎