Capítulo 17 Regresión

Hasta ahora, este libro se ha enfocado principalmente en variables individuales. Sin embargo, en aplicaciones de ciencia de datos, es muy común estar interesado en la relación entre dos o más variables. Por ejemplo, en el Capítulo 18, utilizaremos un enfoque basado en datos que examina la relación entre las estadísticas de los jugadores y el éxito para guiar la construcción de un equipo de béisbol con un presupuesto limitado. Antes de profundizar en este ejemplo más complejo, presentamos los conceptos necesarios para entender la regresión utilizando una ilustración más sencilla. De hecho, utilizamos el set de datos con el cual se inventó la regresión.

El ejemplo es de la genética. Francis Galton⁶⁹ estudió la variación y la herencia de los rasgos humanos. Entre muchos otros rasgos, Galton recopiló y estudió datos de estatura de familias para tratar de entender la herencia. Mientras hacía eso, desarrolló los conceptos de correlación y regresión, así como una conexión a pares de datos que siguen una distribución normal. Por supuesto, en el momento en que se recopilaron estos datos, nuestro conocimiento de la genética era bastante limitado en comparación con lo que sabemos hoy. Una pregunta muy específica que Galton intentó contestar fue: ¿cuán bien podemos predecir la altura de un niño basándose en la altura de los padres? La técnica que desarrolló para responder a esta pregunta, la regresión, también se puede aplicar a nuestra pregunta de béisbol y a muchas otras circunstancias.

Nota histórica: Galton hizo importantes contribuciones a las estadísticas y la genética, pero también fue uno de los primeros defensores de la eugenesia, un movimiento filosófico científicamente defectuoso favorecido por muchos biólogos de la época de Galton, pero con terribles consecuencias históricas⁷⁰.

17.1 Estudio de caso: ¿la altura es hereditaria?

Tenemos acceso a los datos de altura familiar de Galton a través del paquete HistData. Estos datos contienen alturas de varias docenas de familias: madres, padres, hijas e hijos. Para imitar el análisis de Galton, crearemos un set de datos con las alturas de los padres y un hijo de cada familia seleccionado al azar:

library(tidyverse)
library(HistData)
data("GaltonFamilies")

set.seed(1983)
galton_heights <- GaltonFamilies |>
  filter(gender == "male") |>
  group_by(family) |>
  sample_n(1) |>
  ungroup() |>
  select(father, childHeight) |>
  rename(son = childHeight)

En los ejercicios, veremos otras relaciones, incluyendo la de madres e hijas.

Supongan que nos piden que resumamos los datos de padre e hijo. Dado que ambas distribuciones están bien aproximadas por la distribución normal, podríamos usar los dos promedios y las dos desviaciones estándar como resúmenes:

galton_heights |>
  summarize(mean(father), sd(father), mean(son), sd(son))
#> # A tibble: 1 × 4
#>   `mean(father)` `sd(father)` `mean(son)` `sd(son)`
#>            <dbl>        <dbl>       <dbl>     <dbl>
#> 1           69.1         2.55        69.2      2.71

Sin embargo, este resumen no describe una característica importante de los datos: la tendencia de que entre más alto es el padre, más alto es el hijo.

galton_heights |> ggplot(aes(father, son)) +
  geom_point(alpha = 0.5)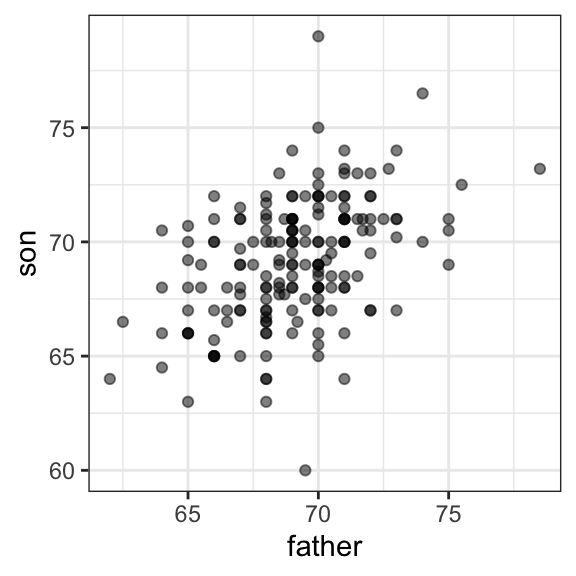

Aprenderemos que el coeficiente de correlación es un resumen informativo de cómo dos variables se mueven juntas y luego veremos cómo esto se puede usar para predecir una variable usando la otra.

17.2 El coeficiente de correlación

El coeficiente de correlación se define para una lista de pares \((x_1, y_1), \dots, (x_n,y_n)\) como el promedio del producto de los valores estandarizados:

\[ \rho = \frac{1}{n} \sum_{i=1}^n \left( \frac{x_i-\mu_x}{\sigma_x} \right)\left( \frac{y_i-\mu_y}{\sigma_y} \right) \] con \(\mu_x, \mu_y\) los promedios de \(x_1,\dots, x_n\) y \(y_1, \dots, y_n\), respectivamente, y \(\sigma_x, \sigma_y\) las desviaciones estándar. La letra griega para \(r\), \(\rho\), se usa comúnmente en libros de estadística para denotar la correlación porque es la primera letra de la palabra regresión. Pronto aprenderemos sobre la conexión entre correlación y regresión. Podemos representar la fórmula anterior con código R usando:

rho <- mean(scale(x) * scale(y))

Para entender por qué esta ecuación resume cómo se mueven juntas dos variables, consideren que la entrada número \(i\) de \(x\) está \(\left( \frac{x_i-\mu_x}{\sigma_x} \right)\) desviaciones estándar del promedio \(\mu_x\). Del mismo modo, el \(y_i\) que se combina con \(x_i\), está \(\left( \frac{y_1-\mu_y}{\sigma_y} \right)\) desviaciones estándar del promedio \(\mu_y\). Si \(x\) e \(y\) no están relacionadas, el producto \(\left( \frac{x_i-\mu_x}{\sigma_x} \right)\left( \frac{y_i-\mu_y}{\sigma_y} \right)\) será positivo (\(+ \times +\) y \(- \times -\)) tan frecuentemente como negativo (\(+ \times -\) y \(- \times +\)) y tendrá un promedio de alrededor de 0. La correlación es el promedio de estos productos y, por lo tanto, las variables no relacionadas tendrán correlación 0. En cambio, si las cantidades varían juntas, entonces estamos promediando productos mayormente positivos (\(+ \times +\) y \(- \times -\)) y obtenemos una correlación positiva. Si varían en direcciones opuestas, obtenemos una correlación negativa.

El coeficiente de correlación siempre está entre -1 y 1. Podemos mostrar esto matemáticamente: consideren que no podemos tener una correlación más alta que cuando comparamos una lista consigo misma (correlación perfecta) y, en este caso, la correlación es:

\[ \rho = \frac{1}{n} \sum_{i=1}^n \left( \frac{x_i-\mu_x}{\sigma_x} \right)^2 = \frac{1}{\sigma_x^2} \frac{1}{n} \sum_{i=1}^n \left( x_i-\mu_x \right)^2 = \frac{1}{\sigma_x^2} \sigma^2_x = 1 \]

Una derivación similar, pero con \(x\) y su opuesto exacto, prueba que la correlación tiene que ser mayor o igual a -1.

Para otros pares, la correlación está entre -1 y 1. La correlación entre las alturas de padre e hijo es de aproximadamente 0.5:

galton_heights |> summarize(r = cor(father, son)) |> pull(r)
#> [1] 0.433

Para ver cómo se ven los datos para diferentes valores de \(\rho\), aquí tenemos seis ejemplos de pares con correlaciones que van desde -0.9 a 0.99:

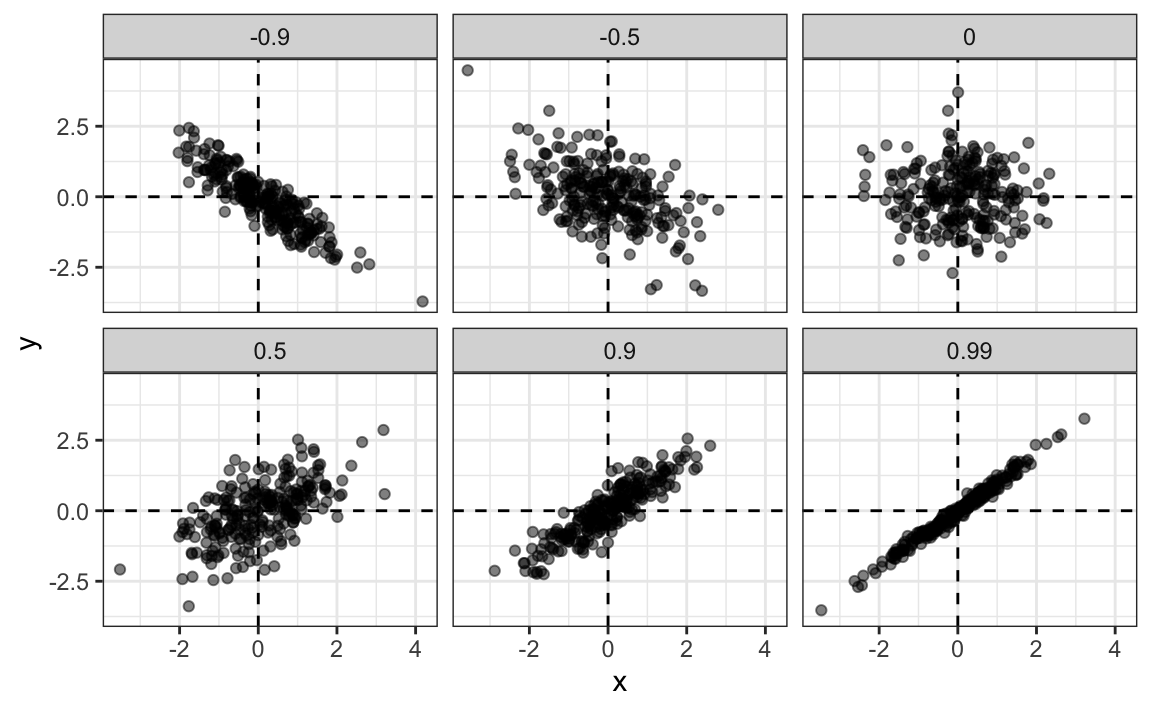
17.2.1 La correlación de muestra es una variable aleatoria

Antes de continuar conectando la correlación con la regresión, recordemos la variabilidad aleatoria.

En la mayoría de las aplicaciones de ciencia de datos, observamos datos que incluyen variación aleatoria. Por ejemplo, en muchos casos, no observamos datos para toda la población de interés, sino para una muestra aleatoria. Al igual que con la desviación promedio y estándar, la correlación de muestra (sample correlation en inglés) es el estimador más comúnmente utilizado de la correlación de la población. Esto implica que la correlación que calculamos y usamos como resumen es una variable aleatoria.

A modo de ilustración, supongan que los 179 pares de padres e hijos es toda nuestra población. Un genetista menos afortunado solo puede permitirse mediciones de una muestra aleatoria de 25 pares. La correlación de la muestra se puede calcular con:

R <- sample_n(galton_heights, 25, replace = TRUE) |>
  summarize(r = cor(father, son)) |> pull(r)

R es una variable aleatoria. Podemos ejecutar una simulación Monte Carlo para ver su distribución:

B <- 1000
N <- 25
R <- replicate(B, {
  sample_n(galton_heights, N, replace = TRUE) |>
    summarize(r=cor(father, son)) |>
    pull(r)
})
qplot(R, geom = "histogram", binwidth = 0.05, color = I("black"))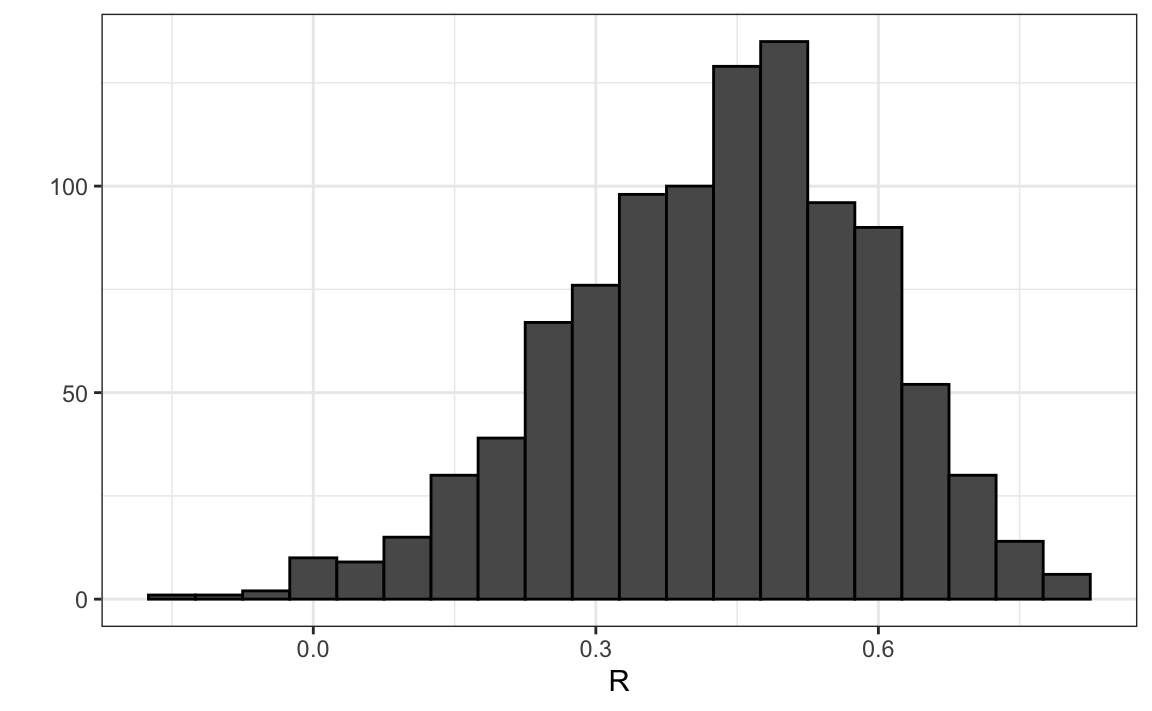

Vemos que el valor esperado de R es la correlación de la población:

mean(R)
#> [1] 0.431

y que tiene un error estándar relativamente alto en relación con el rango de valores que R puede tomar:

sd(R)
#> [1] 0.161

Entonces, al interpretar las correlaciones, recuerden que las correlaciones derivadas de las muestras son estimadores que contienen incertidumbre.

Además, tengan en cuenta que debido a que la correlación de la muestra es un promedio de sorteos independientes, el límite central aplica. Por lo tanto, para \(N\) suficientemente grande, la distribución de R es aproximadamente normal con valor esperado \(\rho\). La desviación estándar, que es algo compleja para derivar, es \(\sqrt{\frac{1-r^2}{N-2}}\).

En nuestro ejemplo, \(N=25\) no parece ser lo suficientemente grande como para que la aproximación sea buena:

ggplot(aes(sample=R), data = data.frame(R)) +
  stat_qq() +
  geom_abline(intercept = mean(R), slope = sqrt((1-mean(R)^2)/(N-2)))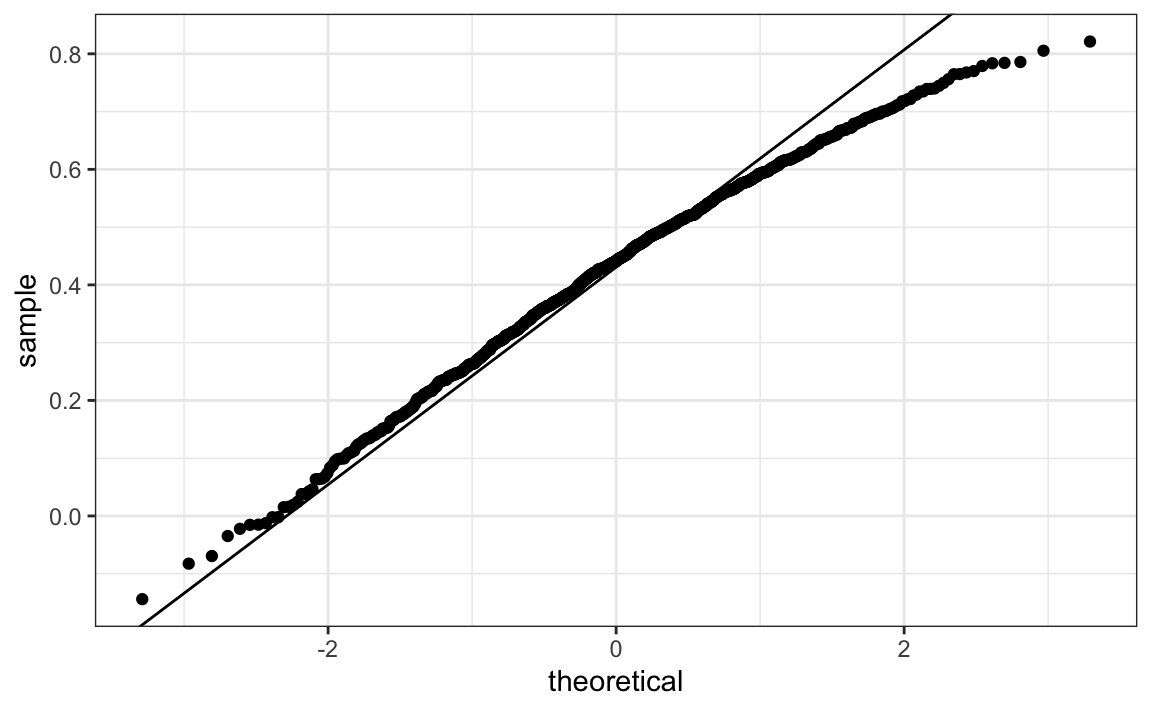

Si aumentan \(N\), verán que la distribución converge a la normalidad.

17.2.2 La correlación no siempre es un resumen útil

La correlación no siempre es un buen resumen de la relación entre dos variables. Los siguientes cuatro sets de datos artificiales, conocidos como el cuarteto de Anscombe, ilustran este punto. Todos estos pares tienen una correlación de 0.82:

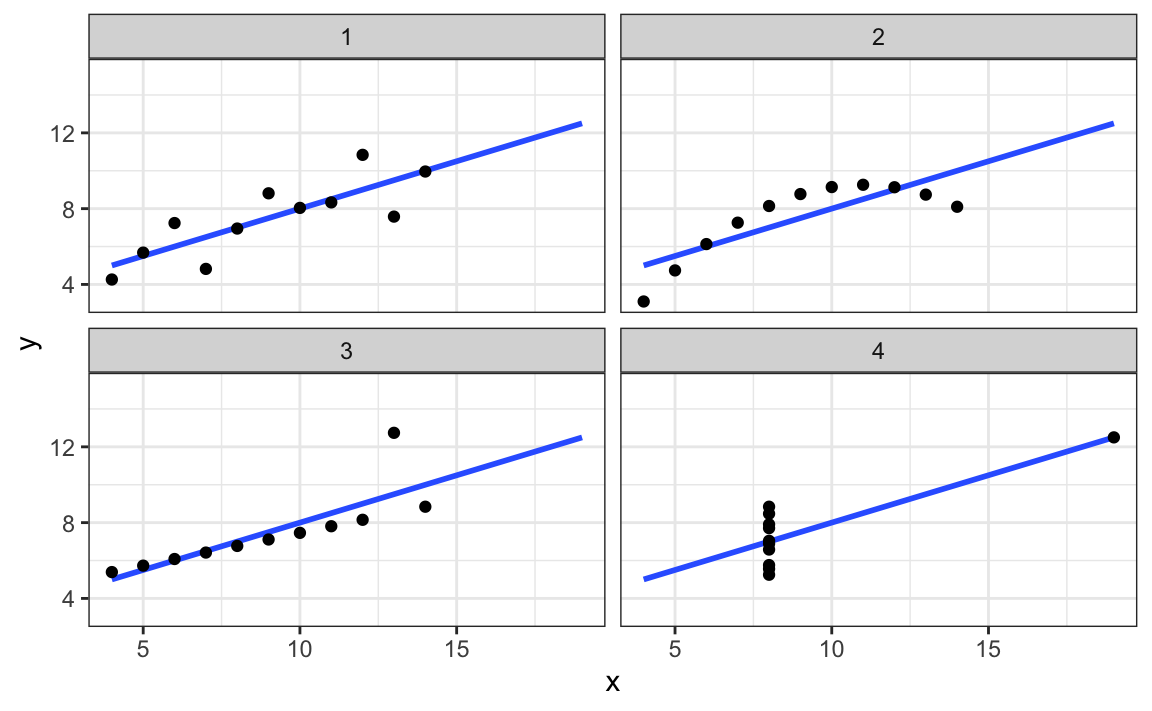
La correlación solo tiene sentido en un contexto particular. Para ayudarnos a entender cuándo la correlación tiene sentido como resumen estadístico, volveremos al ejemplo de predecir la altura de un hijo usando la altura de su padre. Esto ayudará a motivar y definir la regresión lineal. Comenzamos demostrando cómo la correlación puede ser útil para la predicción.

17.3 Valor esperado condicional

Supongan que se nos pide que adivinemos la altura de un hijo, seleccionado al azar, y no sabemos la altura de su padre. Debido a que la distribución de las alturas de los hijos es aproximadamente normal, conocemos que la altura promedio, 69.2, es el valor con la mayor proporción y sería la predicción con la mayor probabilidad de minimizar el error. Pero, ¿qué pasa si nos dicen que el padre es más alto que el promedio, digamos que mide 72 pulgadas, todavía adivinaríamos 69.2 para el hijo?

Resulta que si pudiéramos recopilar datos de un gran número de padres que miden 72 pulgadas, la distribución de las alturas de sus hijos sigue una distribución normal. Esto implica que el promedio de la distribución calculada en este subconjunto sería nuestra mejor predicción.

En general, llamamos a este enfoque condicionar (conditioning en inglés). La idea general es que estratificamos una población en grupos y calculamos resúmenes para cada grupo. Por lo tanto, condicionar está relacionado con el concepto de estratificación descrito en la Sección 8.13. Para proveer una descripción matemática del condicionamiento, consideren que tenemos una población de pares de valores \((x_1,y_1),\dots,(x_n,y_n)\), por ejemplo, todas las alturas de padres e hijos en Inglaterra. En el capítulo anterior, aprendimos que si tomamos un par aleatorio \((X,Y)\), el valor esperado y el mejor predictor de \(Y\) es \(\mbox{E}(Y) = \mu_y\), el promedio de la población \(1/n\sum_{i=1}^n y_i\). Sin embargo, ya no estamos interesados en la población general, sino en el subconjunto de la población con un valor específico de \(x_i\), 72 pulgadas en nuestro ejemplo. Este subconjunto de la población también es una población y, por lo tanto, los mismos principios y propiedades que hemos aprendido aplican. Los \(y_i\) en la subpoblación tienen una distribución, denominada distribución condicional (conditional distribution en inglés), y esta distribución tiene un valor esperado denominado valor esperado condicional (conditional expectation en inglés). En nuestro ejemplo, el valor esperado condicional es la altura promedio de todos los hijos en Inglaterra con padres que miden 72 pulgadas. La notación estadística para el valor esperado condicional es:

\[ \mbox{E}(Y \mid X = x) \]

con \(x\) representando el valor fijo que define ese subconjunto, por ejemplo, en nuestro caso 72 pulgadas. Del mismo modo, denotamos la desviación estándar de los estratos con:

\[ \mbox{SD}(Y \mid X = x) = \sqrt{\mbox{Var}(Y \mid X = x)} \]

Como el valor esperado condicional \(E(Y\mid X=x)\) es el mejor predictor para la variable aleatoria \(Y\) para un individuo en los estratos definidos por \(X=x\), muchos retos de la ciencia de datos se reducen a los estimadores de esta cantidad. La desviación estándar condicional cuantifica la precisión de la predicción.

En el ejemplo que hemos estado considerando, queremos calcular la altura promedio del hijo condicionado en que el padre mida 72 pulgadas. Queremos estimar \(E(Y|X=72)\) utilizando la muestra recopilada por Galton. Anteriormente aprendimos que el promedio de la muestra es el enfoque preferido para estimar el promedio de la población. Sin embargo, un reto al usar este enfoque para estimar los valores esperados condicionales es que para los datos continuos no tenemos muchos puntos de datos que coincidan exactamente con un valor en nuestra muestra. Por ejemplo, solo tenemos:

sum(galton_heights$father == 72)
#> [1] 8

padres que miden exactamente 72 pulgadas. Si cambiamos el número a 72.5, obtenemos aún menos puntos de datos:

sum(galton_heights$father == 72.5)
#> [1] 1

Una forma práctica de mejorar estos estimadores de los valores esperados condicionales es definir estratos con valores similares de \(x\). En nuestro ejemplo, podemos redondear las alturas del padre a la pulgada más cercana y suponer que todas son 72 pulgadas. Si hacemos esto, terminamos con la siguiente predicción para el hijo de un padre que mide 72 pulgadas:

conditional_avg <- galton_heights |>
  filter(round(father) == 72) |>
  summarize(avg = mean(son)) |>
  pull(avg)
conditional_avg
#> [1] 70.5

Noten que un padre que mide 72 pulgadas es más alto que el promedio, específicamente (72.0 - 69.1)/2.5 = 1.1 desviaciones estándar más alto que el padre promedio. Nuestra predicción 70.5 también es más alta que el promedio, pero solo 0.49 desviaciones estándar más que el hijo promedio. Los hijos de padres que miden 72 pulgadas han retrocedido (regressed en inglés) un poco hacia la altura promedio. Observamos que la reducción en la cantidad de desviaciones estandár es de aproximadamente 0.5, que es la correlación. Como veremos en una sección posterior, esto no es una coincidencia.

Si queremos hacer una predicción de cualquier altura, no solo 72 pulgadas, podríamos aplicar el mismo enfoque a cada estrato. La estratificación seguida por diagramas de caja nos permite ver la distribución de cada grupo:

galton_heights |> mutate(father_strata = factor(round(father))) |>
  ggplot(aes(father_strata, son)) +
  geom_boxplot() +
  geom_point()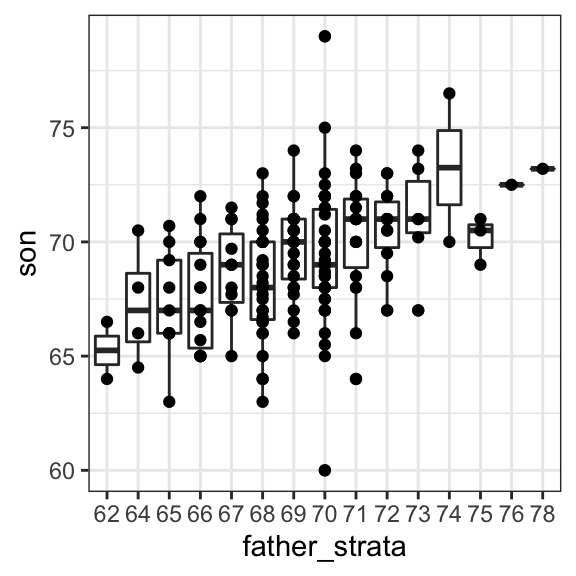

No es sorprendente que los centros de los grupos estén aumentando con la altura. Además, estos centros parecen seguir una relación lineal. A continuación graficamos los promedios de cada grupo. Si tomamos en cuenta que estos promedios son variables aleatorias con errores estándar, los datos son consistentes con estos puntos siguiendo una línea recta:

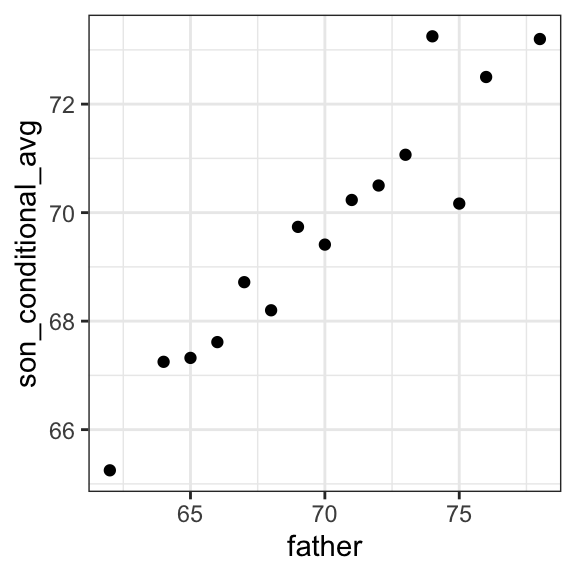
El hecho de que estos promedios condicionales sigan una línea no es una coincidencia. En la siguiente sección, explicamos que la línea que siguen estos promedios es lo que llamamos la línea de regresión (regression line en inglés), que mejora la precisión de nuestros estimadores. Sin embargo, no siempre es apropiado estimar los valores esperados condicionales con la línea de regresión, por lo que también describimos la justificación teórica de Galton para usar la línea de regresión.

17.4 La línea de regresión

Si estamos prediciendo una variable aleatoria \(Y\) sabiendo el valor de otra variable \(X=x\) y usando una línea de regresión, entonces predecimos que por cada desviación estándar \(\sigma_X\) que \(x\) aumenta por encima del promedio \(\mu_X\), \(Y\) aumenta \(\rho\) desviaciones estándar \(\sigma_Y\) por encima del promedio \(\mu_Y\) con \(\rho\) la correlación entre \(X\) y \(Y\). Por lo tanto, la fórmula para la regresión es:

\[ \left( \frac{Y-\mu_Y}{\sigma_Y} \right) = \rho \left( \frac{x-\mu_X}{\sigma_X} \right) \]

Podemos reescribirla así:

\[ Y = \mu_Y + \rho \left( \frac{x-\mu_X}{\sigma_X} \right) \sigma_Y \]

Si hay una correlación perfecta, la línea de regresión predice un aumento que es el mismo número de desviaciones estandár. Si hay 0 correlación, entonces no usamos \(x\) para la predicción y simplemente predecimos el promedio \(\mu_Y\). Para valores entre 0 y 1, la predicción está en algún punto intermedio. Si la correlación es negativa, predecimos una reducción en vez de un aumento.

Tengan en cuenta que si la correlación es positiva e inferior a 1, nuestra predicción está más cerca, en unidades estándar, de la altura promedio que el valor utilizado para predecir, \(x\), está del promedio de las \(x\)s. Es por eso que lo llamamos regresión: el hijo retrocede a la altura promedio. De hecho, el título del artículo de Galton era: Regression towards mediocrity in hereditary stature. Para añadir líneas de regresión a los gráficos, necesitaremos la siguiente versión de la fórmula anterior:

\[ y= b + mx \mbox{ with slope } m = \rho \frac{\sigma_y}{\sigma_x} \mbox{ and intercept } b=\mu_y - m \mu_x \]

Aquí añadimos la línea de regresión a los datos originales:

mu_x <- mean(galton_heights$father)
mu_y <- mean(galton_heights$son)
s_x <- sd(galton_heights$father)
s_y <- sd(galton_heights$son)
r <- cor(galton_heights$father, galton_heights$son)

galton_heights |>
  ggplot(aes(father, son)) +
  geom_point(alpha = 0.5) +
  geom_abline(slope = r * s_y/s_x, intercept = mu_y - r * s_y/s_x * mu_x)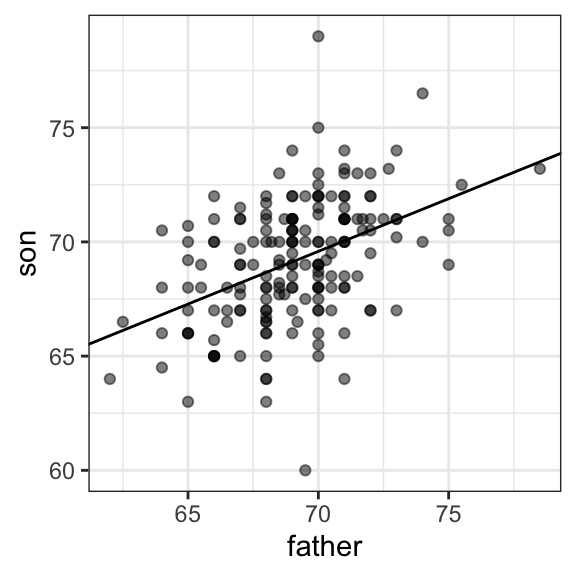

La fórmula de regresión implica que si primero estandarizamos las variables, es decir, restamos el promedio y dividimos por la desviación estándar, entonces la línea de regresión tiene un intercepto 0 y una pendiente igual a la correlación \(\rho\). Pueden hacer el mismo gráfico, pero usando unidades estándar así:

galton_heights |>
  ggplot(aes(scale(father), scale(son))) +
  geom_point(alpha = 0.5) +
  geom_abline(intercept = 0, slope = r)

17.4.1 La regresión mejora la precisión

Comparemos los dos enfoques de predicción que hemos presentado:

Redondear las alturas de los padres a la pulgada más cercana, estratificar y luego tomar el promedio.
Calcular la línea de regresión y usarla para predecir.

Utilizamos una simulación Monte Carlo que muestrea \(N=50\) familias:

B <- 1000
N <- 50

set.seed(1983)
conditional_avg <- replicate(B, {
  dat <- sample_n(galton_heights, N)
  dat |> filter(round(father) == 72) |>
    summarize(avg = mean(son)) |>
    pull(avg)
})

regression_prediction <- replicate(B, {
  dat <- sample_n(galton_heights, N)
  mu_x <- mean(dat$father)
  mu_y <- mean(dat$son)
  s_x <- sd(dat$father)
  s_y <- sd(dat$son)
  r <- cor(dat$father, dat$son)
  mu_y + r*(72 - mu_x)/s_x*s_y
})

Aunque el valor esperado de estas dos variables aleatorias es casi el mismo:

mean(conditional_avg, na.rm = TRUE)
#> [1] 70.5
mean(regression_prediction)
#> [1] 70.5

El error estándar para la predicción usando la regresión es sustancialmente más pequeño:

sd(conditional_avg, na.rm = TRUE)
#> [1] 0.964
sd(regression_prediction)
#> [1] 0.452

La línea de regresión es, por lo tanto, mucho más estable que la media condicional. Hay una razón intuitiva para esto. El promedio condicional se basa en un subconjunto relativamente pequeño: los padres que miden aproximadamente 72 pulgadas. De hecho, en algunas de las permutaciones no tenemos datos, por eso utilizamos na.rm=TRUE. La regresión siempre usa todos los datos.

Entonces, ¿por qué no siempre usar la regresión para predecir? Porque no siempre es apropiado. Por ejemplo, Anscombe ofreció casos para los cuales los datos no tienen una relación lineal. Entonces, ¿tiene sentido usar la línea de regresión para predecir en nuestro ejemplo? Galton encontró que sí, en el caso de los datos de altura. La justificación, que incluimos en la siguiente sección, es algo más avanzada que el resto del capítulo.

17.4.2 Distribución normal de dos variables (avanzada)

La correlación y la pendiente de regresión son resumenes estadísticos ampliamente utilizados, pero que a menudo se malinterpretan o se usan mal. Los ejemplos de Anscombe ofrecen casos simplificados de sets de datos en los que resumir con correlación sería un error. Sin embargo, hay muchos más ejemplos de la vida real.

La manera principal en que motivamos el uso de la correlación involucra lo que se llama la distribución normal de dos variables (bivariate normal distribution en inglés).

Cuando un par de variables aleatorias se aproxima por la distribución normal de dos variables, los diagramas de dispersión parecen óvalos. Como vimos en la Sección 17.2, pueden ser delgados (alta correlación) o en forma de círculo (sin correlación).

Una forma más técnica de definir la distribución normal de dos variables es la siguiente: si \(X\) es una variable aleatoria normalmente distribuida, \(Y\) también es una variable aleatoria normalmente distribuida, y la distribución condicional de \(Y\) para cualquier \(X=x\) es aproximadamente normal, entonces el par sigue una distribución normal de dos variables.

Si creemos que los datos de altura están bien aproximados por la distribución normal de dos variables, entonces deberíamos ver que la aproximación normal aplica a cada estrato. Aquí estratificamos las alturas de los hijos por las alturas estandarizadas de los padres y vemos que el supuesto parece ser válido:

galton_heights |>
  mutate(z_father = round((father - mean(father))/ sd(father))) |>
  filter(z_father %in% -2:2) |>
  ggplot() +
  stat_qq(aes(sample = son)) +
  facet_wrap( ~ z_father)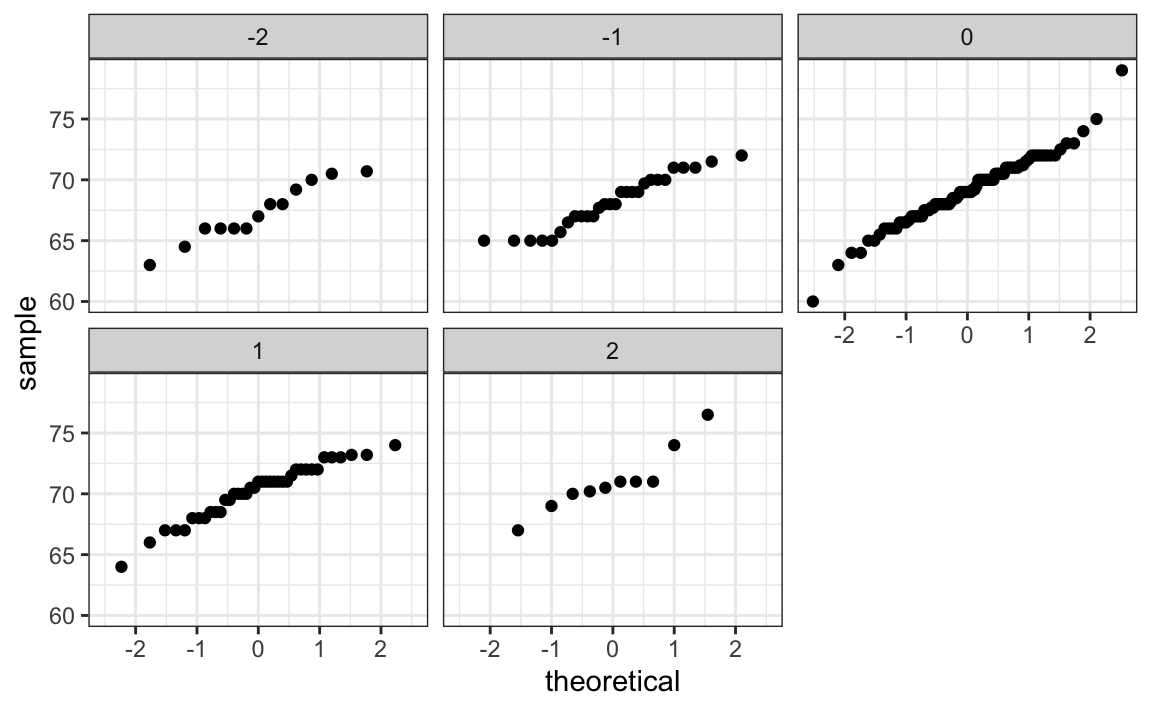

Ahora volvemos a tratar de definir correlación. Galton utilizó estadísticas matemáticas para demostrar que, cuando dos variables siguen una distribución normal de dos variables, calcular la línea de regresión es equivalente a calcular los valores esperados condicionales. No mostramos la derivación aquí, pero podemos mostrar que bajo este supuesto, para cualquier valor dado de \(x\), el valor esperado de \(Y\) en pares para los cuales \(X=x\) es:

\[ \mbox{E}(Y | X=x) = \mu_Y + \rho \frac{X-\mu_X}{\sigma_X}\sigma_Y \]

Esta es la línea de regresión, con pendiente: \[\rho \frac {\sigma_Y} {\sigma_X}\]

e intercepto \(\mu_y - m\mu_X\). Es equivalente a la ecuación de regresión que mostramos anteriormente que se puede escribir así:

\[ \frac{\mbox{E}(Y \mid X=x) - \mu_Y}{\sigma_Y} = \rho \frac{x-\mu_X}{\sigma_X} \]

Esto implica que, si la distribución de nuestros datos se puede aproximar con una distribución normal de dos variables, la línea de regresión da el valor esperado condicional. Por lo tanto, podemos obtener un estimador mucho más estable del valor esperado condicional al encontrar la línea de regresión y usarla para predecir.

En resumen, si nuestros datos se pueden aproximar con una distribución normal de dos variables, entonces el valor esperado condicional, la mejor predicción de \(Y\) cuando sabemos el valor de \(X\), lo da la línea de regresión.

17.4.3 Varianza explicada

La teoría de la distribución normal de dos variables también nos dice que la desviación estándar de la distribución condicional descrita anteriormente es:

\[ \mbox{SD}(Y \mid X=x ) = \sigma_Y \sqrt{1-\rho^2} \]

Para ver por qué esto es intuitivo, observen que sin condicionar, \(\mbox{SD}(Y) = \sigma_Y\), estamos viendo la variabilidad de todos los hijos. Pero tan pronto condicionamos, solo observamos la variabilidad de los hijos con un padre alto, de 72 pulgadas. Este grupo tenderá a ser algo alto, por lo que se reduce la desviación estándar.

Específicamente, se reduce a \(\sqrt{1-\rho^2} = \sqrt{1 - 0.25}\) = 0.87 de lo que era originalmente. Podríamos decir que las alturas de los padres “explican” el 13% de la variabilidad observada en las alturas de los hijos.

La declaración “\(X\) explica tal y cual porcentaje de la variabilidad” se usa comúnmente en los trabajos académicos. En este caso, este porcentaje realmente se refiere a la varianza (la desviación estándar al cuadrado). Entonces si los datos siguen una distribución normal de dos variables, la varianza se reduce por \(1-\rho^2\) y entonces decimos que \(X\) explica \(1- (1-\rho^2)=\rho^2\) (la correlación al cuadrado) de la varianza.

Pero es importante recordar que la declaración de “varianza explicada” solo tiene sentido cuando los datos se aproximan mediante una distribución normal de dos variables.

17.4.4 Advertencia: hay dos líneas de regresión

Calculamos una línea de regresión para predecir la altura del hijo basada en la altura del padre. Utilizamos estos cálculos:

mu_x <- mean(galton_heights$father)
mu_y <- mean(galton_heights$son)
s_x <- sd(galton_heights$father)
s_y <- sd(galton_heights$son)
r <- cor(galton_heights$father, galton_heights$son)
m_1 <- r * s_y/ s_x
b_1 <- mu_y - m_1*mu_x

que nos da la función \(\mbox{E}(Y\mid X=x) =\) 37.3 + 0.46 \(x\).

¿Qué pasa si queremos predecir la altura del padre basada en la del hijo? Es importante saber que esto no se determina calculando la función inversa: \(x = \{ \mbox{E}(Y\mid X=x) -\) 37.3 \(\}/0.5\).

Necesitamos calcular \(\mbox{E}(X \mid Y=y)\). Dado que los datos se aproximan mediante una distribución normal de dos variables, la teoría descrita anteriormente nos dice que este valor esperado condicional seguirá una línea con pendiente e intercepto:

m_2 <- r * s_x/ s_y
b_2 <- mu_x - m_2 * mu_y

Entonces obtenemos \(\mbox{E}(X \mid Y=y) =40.9 + 0.41y\). Nuevamente vemos una regresión al promedio: la predicción para la altura del padre está más cerca del promedio del padre que la altura del hijo \(y\) está a la altura del hijo promedio.

Aquí tenemos un gráfico que muestra las dos líneas de regresión. La azul predice las alturas de los hijos según las alturas de los padres y la roja predice las alturas de los padres según las alturas de los hijos:

galton_heights |>
  ggplot(aes(father, son)) +
  geom_point(alpha = 0.5) +
  geom_abline(intercept = b_1, slope = m_1, col = "blue") +
  geom_abline(intercept = -b_2/m_2, slope = 1/m_2, col = "red")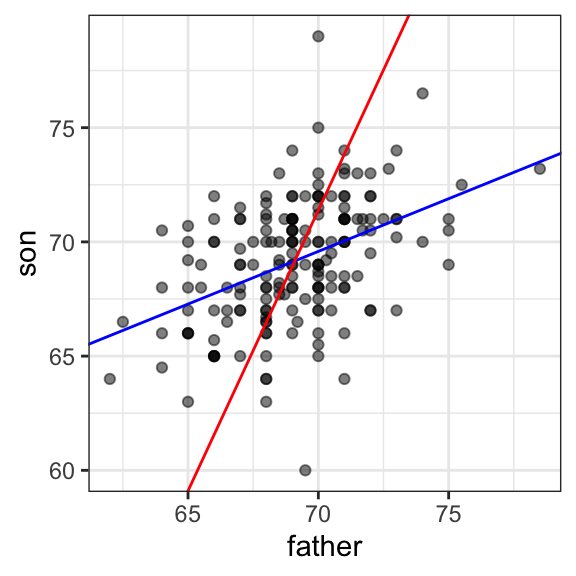

17.5 Ejercicios

1. Cargue los datos GaltonFamilies de HistData. Los niños de cada familia se enumeran por género y luego por estatura. Cree un set de datos llamado galton_heights eligiendo un varón y una hembra al azar.

2. Haga un diagrama de dispersión para las alturas entre madres e hijas, madres e hijos, padres e hijas, y padres e hijos.

3. Calcule la correlación en las alturas entre madres e hijas, madres e hijos, padres e hijas, y padres e hijos.